目录
主成分分析
一、相关说明
遇到的问题
在对现实现象(y)选择解释变量(x)时不难发现有许多变量或多或少的影响,于是就会产生一种局面,即解释变量有许多个(即所说的高维)且解释变量之间也会出现相关性。
例如要对中国的大学进行排名,可以选择的指标有:师资资源、学术资源、财力资源、学生情况、研究成果等,其中财力资源和研究成果之间(财力资源影响着研究成果)有着相关性,携带的信息有重叠。就导致变量太多,信息错综复杂,分析不方便。为了解决这个问题,我们可以将这几个变量转化为综合变量,减少个数且使其不相关。
PCA(主成分分析)的基本思想:将原来有一定相关性的一组指标(如p个指标),重新组合成一组相互无关的p个综合指标代替原来的指标。并用其中较少的几个新指标变量综合反映原p个指标变量中所包含的主要信息,符合专业含义。(降维度、弱相关)
原始变量:,经过转化,成 主成分:
,且为线性组合;信息不重叠(C1,C2,...,Cp不相关);按“重要性”排序。
如何解决
1.弱相关

如图,两个坐标系,一个是原图坐标系(x1,x2),另一个新建立的坐标系(,
,在那些散点上的两条相互垂直的线,一长一短),其中长线是这些数据组成的点的回归线,由线性代数相关知识得,旋转坐标轴后所得到的新的变量
,
,相互垂直且无相关性(正交)。
在主成分分析中,具体操作为将原来的p个指标做线性组合,形成具有代表性的新综合指标。
第一个综合指标。我们知道C1是原始变量的线性组合,为了让他具有代表性,要使其方差最大,所以在取
时要能够使C1的方差最大。
第二个综合指标 :,
的取法要满足:
(1) 使得C2的方差var(C2)次大;(2) 要求C2与C1不相关,cov(C1,C2)=0,即正交。
这些新的指标(变量)按照方差依次递减的顺序排列。以此类推,可创建第三,第四,….,第p个指标,同时后面的指标要与前面的指标是正交的。
第一指标(变量)称为第一主成分,第二指标(变量)称为第二主成分。依次类推。

2.降维
在选择指标的时候,我们知道要选择具有代表性的指标,即差异大,波动大的。长轴波动大,差异大,短轴上差异小。
一般结论:被选的主成分所代表的主轴的长度之和占了主轴长度总和的大部分。有些文献建议,所选的主轴总长度占所有主轴长度之和的大约80%即可(也可85%),就可以说缺损度不大,可降维。即若其中一个的方差占全部的80%(或85%)以上,就说明他的代表性强以至于可以忽略其他一些代表性弱的。
但由于指标间存在差异,在求方差时会影响取值(例如1,2,3与0.1,0.2,0.3,占比都一样但是方差不一样),于是我们要将其标准化()之后再比较:


Xj是个向量。


特征值:
每个特征值对应的特征向量无关且正交。

贡献率:信息的比例。

二、代码及解读



注:x1—x13是x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12,x13的简写。
princomp是“Principal Components Procedure”的缩写,意即主成分分析。
out表示输出到prin这个数据集。
date表示打印出prin(prin1到prin13个主成分来)
结果为

Eigenvalue是特征值,Difference是两个主成分的差,Proportion是贡献率,Cumulative是累计贡献率
前三个特征根累计解释方差的比率已经超过了94%(>85%),说明提取三个主成分即可代表原始数据的大部分信息。
Tips:为什么选了三个,正常两个就好:1.信息更多,2.方便做主成分回归(在多元回归中,原则是样本数要比1+3*变量个数大,及13>3p+1,所以p取3)

X1,X2,X3,...,都是列向量
可根据主成分计算公式中的系数,即主成分载荷绝对值的大小来判定该主成分主要代表的原始变量的含义,绝对值越大,对应的变量与主成分关系密切。
第一主成分与蔬菜种植面积(x1)、每公顷物质费用(x2)蔬菜零售物价指数(x4)、市场化程度(x6)、城市化水平1(x7),城市化水平(x8)、交通、城镇居民可支配收入(x9)、农村居民纯收入(x10)、农民文化素质(x11)等密切相关,表示的是市场经济综合因素,着重反映的是市场经济的成熟程度与国家现代化水平
第二主成分与每公顷劳动投入(x3)、成本纯收益率(x5)等密切相关,表示的是劳动者动力因素
第三主成分与气候条件(x13)密切相关,显然表示的是气候因素。
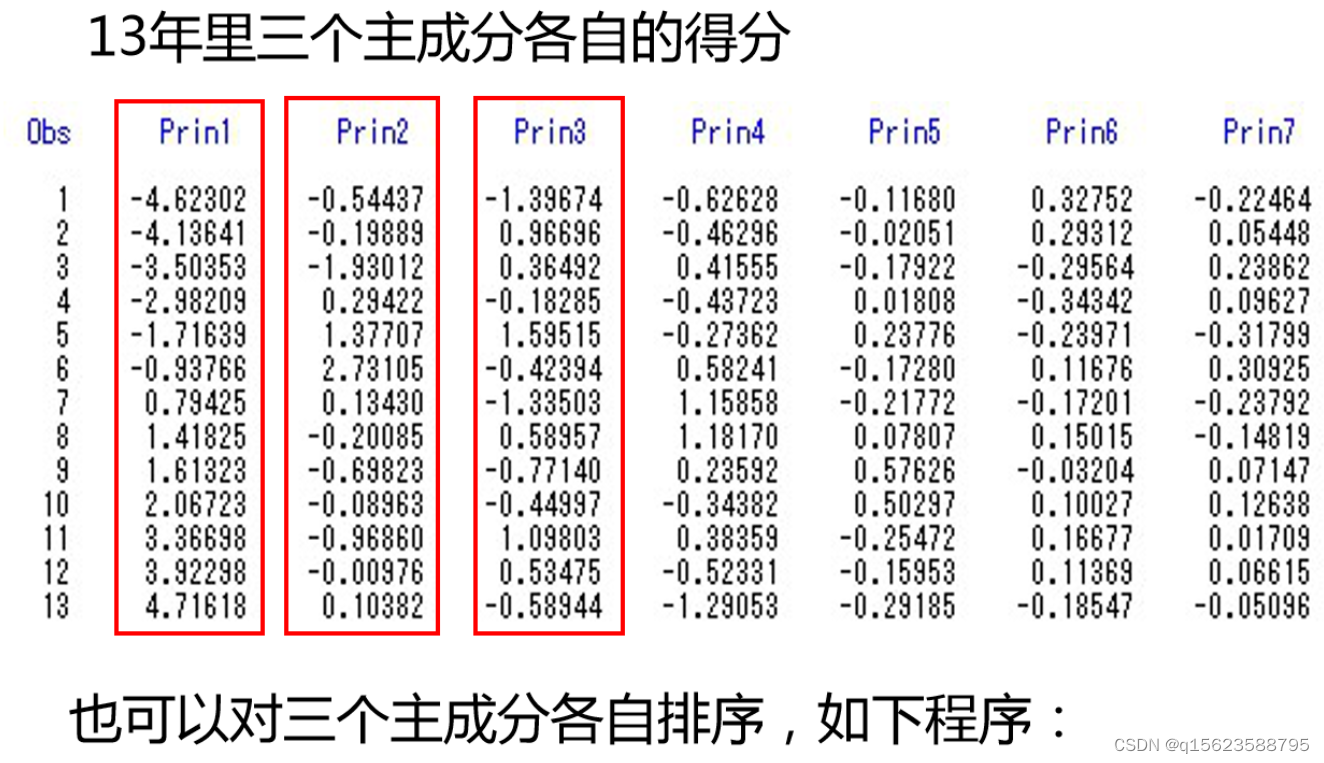


最后可以利用贡献率(特征根)及其对应的主成分得分计算出综合得分(每年的)
(综合得分(第i个主成分贡献率*第i个主成分得分))
如例中的综合得分公式为:综合得分=第一主成分得分x0.7818+第二主成分得分x0.0962+第三主成分得分x0.0676

之后算出最大的是哪一个
三、例题














 本文介绍了主成分分析(PCA)在处理高维相关数据中的应用,包括如何通过线性组合减少变量数量,消除相关性,以及如何确定主成分和降维的准则。通过实例展示了如何利用PCA提取关键信息,如市场经济、劳动者动力和气候因素,以及如何计算综合得分。
本文介绍了主成分分析(PCA)在处理高维相关数据中的应用,包括如何通过线性组合减少变量数量,消除相关性,以及如何确定主成分和降维的准则。通过实例展示了如何利用PCA提取关键信息,如市场经济、劳动者动力和气候因素,以及如何计算综合得分。
















 6426
6426

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








