SAS入门——非参数统计初学者笔记欢迎指正

q15623588795

已于 2024-05-15 15:51:13 修改

阅读量2.3k

点赞数 22

分类专栏： SAS 文章标签：笔记

于 2024-05-08 14:29:11 首次发布

本文链接：https://blog.csdn.net/q15623588795/article/details/138542816

版权

SAS 专栏收录该内容

6 篇文章

订阅专栏

非参数统计：总体是否相同

非参数检验（non-parametric test）又称为分布自由检验，一种与总体分布状况无关的检验方法，它不依赖于总体分布的形式，应用时可以不考虑被研究的对象为何种分布以及分布是否已知。
非参数检验主要是利用样本数据之间的大小比较及大小顺序，对两个或多个样本所属总体是否相同进行检验，而不对总体分布的参数如平均数、标准差等进行统计推断。

一.两组样本数据的检验

1.符号检验法

配对样本数据符号检验法

设(X1, Y1) (X2, Y2),…, (Xn, Yn)是取自二维总体(X,Y)的配对样本，容量为n，其观测值为(x1, y1) (x2,y2),…, (xn, yn)，当两个分布函数未知时，可用符号检验法检验这两个总体的分布是否有显著的差异

符号检验法的步骤如下：
1.提出假设H0：两个总体的分布相同；
2.计算xi-yi并数出两个差值中符号为正的个数n+及符号为负的个数n- ；（- +为下标）
3.根据α由符号检验用表中查出相应于n(除去xi-yi为0的个数)的Cα；
4.当min(n+ ,n-) ≤Cα时拒绝H0，否则接受H0

将正号的个数与负号的个数进行比较，易知：
如果正号个数和负号个数大致相当，则可以认为第二组样本大于第一组样本变量值的个数，与第二组样本小于第一组样本的变量值个数是大致相当的，从总体上讲，这两个组配对样本的数据分布差距较小；
相反，如果正号个数和负号个数相差较多，则可以认为两个配对样本的数据分布差距较大。

例 1 甲乙两人分析同一物质中某成份的含量，得到观测数据(单位:g)为

试在显著性水平为0.05时用符号检验法检验两人的分析有无显著差异

符号检验法的步骤如下：
1.提出假设H0：两个人的分析无显著性差异；
2.计算xi-yi并统计各个观测值中符号为正的个数n+=5，符号为负的个数n- =4；

3.由符号检验用表中查出相应于9的C0.05=1；
4.当min(n+ ,n-) =4>C0.05，决定接受H0，认为两人的分析无显著性差异

data ex;
input x1 x2 @@;
y=x1-x2;
cards;
14.7 14.6 15.0 15.1 15.2 15.4 14.8 14.7 15.5 15.2 14.6 14.7
14.9 14.8 14.8 14.6 15.1 15.2 15.0 15.0
;
proc univariate;
var y;
run;

UNIVARIATE过程：主要用于对指定随机变量进行详细的描述性统计，输出N(样本量数), MEAN，STD DEV，MIN，MAX等的功能，还可计算其他一些统计量，也可绘制茎叶图，盒形图，正态概率图和计算各种百分位值。

结果输出有4个部分:
(1)结果第一部分包括变量数目有效观测次数N, 均值Mean,总的观测值Sum Observations，标准差Std Deviation, 方差Variance，偏度Skewness，峰度Kurtosis，反修正SS值Uncorrected SS，修正值Corrected SS, 变异系数CoeffVariation和均值标准差 Std Error Mean。
(2)结果第二部分包括均值Mean，中值Median，众数Mode，范围Range

(3)结果第三部分包括检验Test，统计量Statistic，P值p Value。
(4)结果第四部分包括分位数Quantile及估计值Estimate

结果分析: 由Tests for Location: Mu0=0表可知,M(Sign)的值为0.5,pr>M的值为1.0000>0.05,故接受原假设H0，认为两人的分析无显著

一个总体中位数的假设检验

为了判断某个总体的中位数是否与已知数m有显著的差异，也可以用符号检验法
例3 试验品种猪在17个试验点的月增重(单位:kg)见表：试问，月增重与35是否有显著性差异？

data ex; input x @@;
y=x-35;
cards;
51 40 43 48 23 26 30 34
25 40 41 39 42 40 43 30
34
;
proc univariate;
var y;
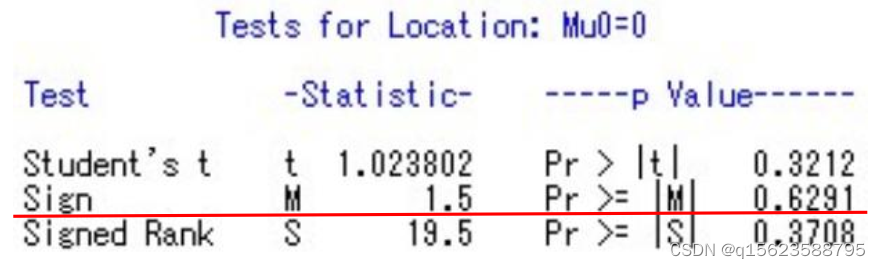
run;

由于运行结果与前例的结果情况类似，本题只选取结果中最重要的部分，即结果第三部分，M(Sign)的值为1.5，Pr >= |M|值为0.6291>0.05，故未落在拒绝域里，因此接受原假设，认为该品种猪月增重的中位数与35无显著差异。

只要具备成对数据，均可利用符号检验作出一个科学的判断。但由于此方法仅利用了符号的信息，故而信息有所损失，且精确度不高。

2.秩和检验法

设总体X和Y都有连续性的分布函数，从两个总体中相互独立的各取一个容量为m的样本X1, X2, …，Xm和一个容量为n的样本Y1，Y2,…, Yn且m≤n，当两个分布函数未知时，可用秩和检验法(又称WilcoxonMann-Whitney检验法，或Mann-Whitney检验法)检验这两个总体的分布是否有显著性的差异。

设X为一总体，将容量为n的样本观察值按自小到大的次序编号排列成x(1) < x(2) < … < x(n)，称x(i)的足标i为x(i)的秩，i = 1,2,…,n。

如果在排列大小时出现了相同大小的观察值, 则其秩的定义为足标的平均值 .
秩和检验是基于样本数据的秩和

原理：

先将两样本看成是单一样本(混合样本)，然后由小到大排列观察值统一编秩。
如果原假设两个独立样本来自相同的总体为真，那么秩将大约均匀分布在两个样本中。
如果两个独立样本来自不相同的总体为真，那么其中一个样本将会有更多的小秩值，这样就会得到一个较小的秩和；另外一个样本将会有更多的大秩值，因此会得到一个较大的秩和。两个总体的秩和会较大的差异。
例测定两个马铃薯品种的淀粉含量(%)，得到A，B两个品种的观测值如下：

试在显著性水平为0.05时用秩和检验法检验两品种的淀粉含量无显著差异。

data ex;
do a=1 to 2;input n @@;
do i=1 to n;input x @@;
output;end;end;
cards;
2 12.6 12.4
6 12.4 12.1 12.5 12.7 12.6 13.1
;
proc npar1way wilcoxon;/*调用npar1way过程进行对因素a的wilcoxon秩和检验*/
/*是数字1，不是字母l*/
class a; var x;
run;
/*n和x表示每组当中的样品个数，在本题中为2，6*/

从运行结果中可知，统计量值S =8，正态分布近似值为Z = -0.1687 ，双侧检验Prob > |Z| =0.8660，t分布近似的P值(two-sided Prob >|Z| )0.8708 。
Kruskal-Wallis Test这一部分，自由度DF为1，Chi-Square value 为Chi-Square 且Prob >ChiSquare 为0.7358>0.05，接受原假设H0，认为两品种的淀粉含量没有显著性差异，淀粉含量相同。

例5 某航空公司的CEO注意到飞离亚特兰大的飞机放弃预订座位的旅客人数在增加，他特别有兴趣想知道，是否从亚特兰大起飞的飞机比从芝加哥起飞的飞机有更多的放弃预订座位的旅客。获得一个从亚特兰大起飞的9次航班和从芝加哥起飞的8次航班上放弃预订座位的旅客人数样本，见表。

data noshows ;
do group=1 to 2;
input n;
do i=1 to n;
input x @@;output;
end;end;
cards;
9
11 15 10 18 11 20 24 22 25
8
13 14 10 8 16 9 17 21
;
proc npar1way data=noshows wilcoxon;
class group;
var x;
run;

二.多组样本数据的检验

1.多组独立样本的H检验法

        方差分析过程关注三个或更多总体的均值是否相等的问题，数据是被假设成具有正态分布和相等的方差，此时检验才能奏效。但有时采集的数据常常不能完全满足这些条件。可使用非参数的Kuskal-Wallis秩和检验，它是对两个以上的秩样本进行比较，本质上它是两样本时的Wilcoxon秩和检验方法在多于两个样本时的推广。
        多组独立样本的H检验法（又称为Kruskal -Wallis单向秩次方差分析法），是检验多组独立样本是否来自同分布总体最常用、功效最强的非参数检验方法。
        它所面对的观测值与作单因素方差分析的观测值相像，只是总体不服从正态分布，也不能近似地服从正态分布，绝大多数情形是无法确定总体的分布

Kruskal – Wallis秩和检验:
1.要求从总体中抽取的样本必须是独立的;
2.将所有样本的值混合在一起看成是单一样本;
3.把这个单一的混合样本值从小到大排序，序列值替换成秩值，最小的值给予秩值1，有相同值则取平均;
4.将数据样本转换成秩样本后，再对这个秩样本进行方差分析。
但此时构造的统计量不是组间平均平方和除以组内平均平方和，而是组间平方和除以全体样本的秩方差

例6 用3种不同的药剂处理水稻种子，发芽后观测到苗高(单位:cm)的观测值如下，试作单向秩次方差分析。

解：①设H0为3组样本来自分布相同的总体；
②n=3×4=12，将各组样本数据混合后由小到大排列，确定各个数据的秩次Rij并计算各组的秩次和Ri，如有相同的数据可同取平均的秩次，结果如下表：

代码如下：

data ex;
do a=1 to 3;do i=1 to 4;
input x @@;
output;end;end;
cards;
21 24 27 20
20 18 19 15
22 25 27 22
;
proc npar1way wilcoxon;
class a;var x;
run;

Kruskal-Wallis Test单向秩次方差分析法检验表，自由度DF值为2，Chi-Squre value为7.2977
Pr> Chi-Squre值为0.0260<0.05,故落在拒绝域里，拒绝原假设，认为3组样本来自分布不相同的总体,即用3种不同的药剂处理水稻种子、发芽后苗高的观测值有显著的差异。

2.多组相关样本的M检验法

M检验法：行均值得分差异分析
功能：检验多组相关样本是否同分布
情形：类似双因素方差分析，但总体(行)分布未知
M检验法的假设：
H0：多个总体的分布相同
H1：多个总体的分布不全相同

例8 有A、B、C、D、E五个工人，请四位上级领导对工人的一天工作日产量给出的满意度评分如下，试检验这五个工人得分有无显著的差异

data ex;
do a=1 to 5; do b=1 to 4; input x @@;
output;end;end;
cards;
85 87 90 80 82 75 81 76 82 86 80 81
79 82 76 75 86 88 86 84
;
proc freq;
tables b*a*x/scores=rank cmh; /*按照SAS的规定，tables b*a*x中b在前、a居中、x在后的位置不可更改*/
run;

分析五位工人的得分是否有显著的差异，主要看行均值得分差异值Row Mean Scores Differ，其值为12.8101且Prob为0.0122<0.05，则拒绝原假设，认为5组样本来自分布不同的总体，即这五位工人的得分有显著的差异。

三.相关性指标与检验

前面介绍了使用非参数方法比较总体的位置或刻度参数，我们同样也可以用非参数方法比较两总体之间的相关问题。秩相关（rank correlation）又称等级相关，它是一种分析和等级间是否相关的方法。
适用于某些不能准确地测量指标值而只能以严重程度、名次先后、反应大小等定出的等级资料，也适用于某些不呈正态分布或难于判断分布的资料。

秩和相关系数

秩和相关系数又称为等级相关系数，是利用两变量的秩次（等级）大小做线性相关分析，对原始变量的分布不作要求，属于非参数统计方法，使用范围较广。
我们主要介绍Spearman秩相关系数与Kendall秩相关系数

Spearman秩相关系数为:

Ri和Qi分别为xi和yi各自在变量X和变量Y中的秩。
当n>=10时，rs的样本分布可以标准化为近似的t分布

Kendall(肯德尔)系数

又称为一致性系数或和谐系数，可反映两组变量的等级或秩相关的程度。

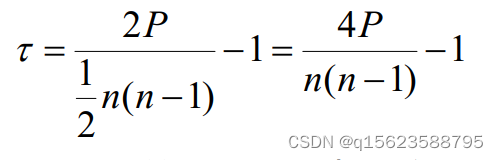
其中n是配对数据的个数，P表示变量Y的一致对数目.
若结果为1，则表示两组秩次完全正相关。-1则完全负相关。

例：调查某个专业篮球队9名球员（包括替补队员）投篮率，弹跳力，球队配合这三个方面能力的等级关系，具体数据见下表：

试分别根据Spearman相关系数和Kendall相关系数分析这三方面能力的等级有无相关关系。

data ex;
input x y @@;
cards;
2 5 6 6 4 3 7 8 3 1 8 7 5 2 1 4 9 9
;
proc corr spearman kendall;
run;

注明：若只求一般的pearson相关系数，只需要运行proc corr即可
从Simple Statistics中可以得出x和y的数量，均值，标准差，中值，最小值及最大值；
从Spearman Correlation Coefficients可得出Spearman相关系数为0.71667，显著性概率为.0298；
从Kendall Tau b Correlation Coefficients得出Kendall相关系数0.55556，显著性概率为0.0371；
从P值可知，投篮率与弹跳率的这两方面能力等级有较高的相关关系

某公司想要知道是否职工期望成为好的销售员而实际上就能有好的销售记录。为了调查这个问题，公司的副总裁仔细地查看和评价了公司10个职工的初始面试摘要、学科成绩、推荐信等材料，最后副总裁根据他们成功的潜能给出了单独的等级评分。二年后获得了实际的销售记录，得到了第二份等级评分，见下表中的第1到4列所示。统计问题为是否职工的销售潜能与开始二年的实际销售成绩一致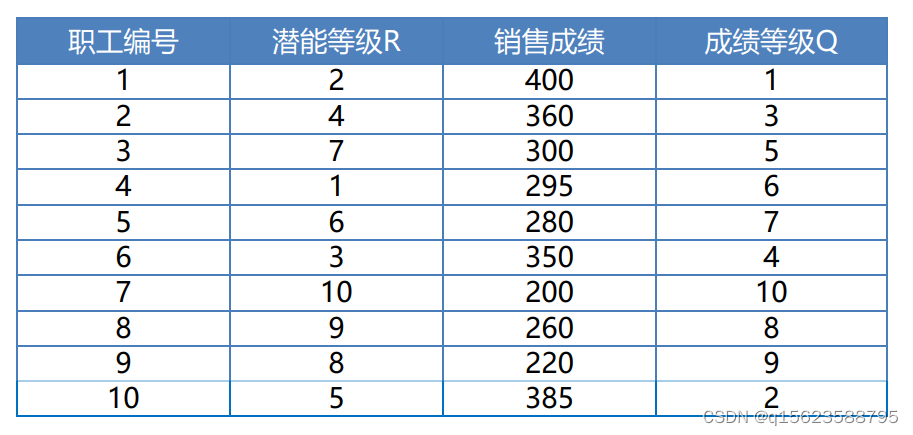

data persons ;
input x y @@;
y=400-y;
cards;
2 400 4 360 7 300 1 295 6 280
3 350 10 200 9 260 8 220 5 385
;
proc corr data=persons spearman;
var x;
with y;
run;