18.双线性插值缩放算法的matlab与FPGA实现（一）

一篇文章为你讲透双线性插值

简介

1.什么是插值

  图片放大是图像处理中的一个特别基础的操作。几乎在每一个图片相关的项目中，从传统图像处理到i深度学习，都有应用。
  简单来说，插值指利用已知的点来“猜”未知的点，图像领域插值常用在修改图像尺寸的过程，由下图是双线性插值的效果。

2.常用的插值算法

  插值算法有很多种，这里列出关联比较密切的三种：
    （1）最近邻法（Nearest Interpolation）：计算速度最快，但是效果最差。
    （2）双线性插值（Bilinear Interpolation）：双线性插值是用原图像中4（2x2）个点计算新图像中1个点，效果略逊于双三次插值，速度比双三次插值快，属于一种平衡美，在很多框架中属于默认算法。
    （3）双三次插值（Bicubic interpolation）：双三次插值是用原图像中16(4x4)个点计算新图像中1个点，效果比较好，但是计算代价过大。

插值算法介绍

2.1最近邻法（Nearest Interpolation）

  最近邻算法不需要计算新图像中矩阵中点的数值，直接找到原图像中对应的点，将数值赋值给新图像矩阵中的点，根据对应关系找到原图像中的对应的坐标，这个坐标可能不是整数；这时候找最近的点进行插值。对应关系如下：

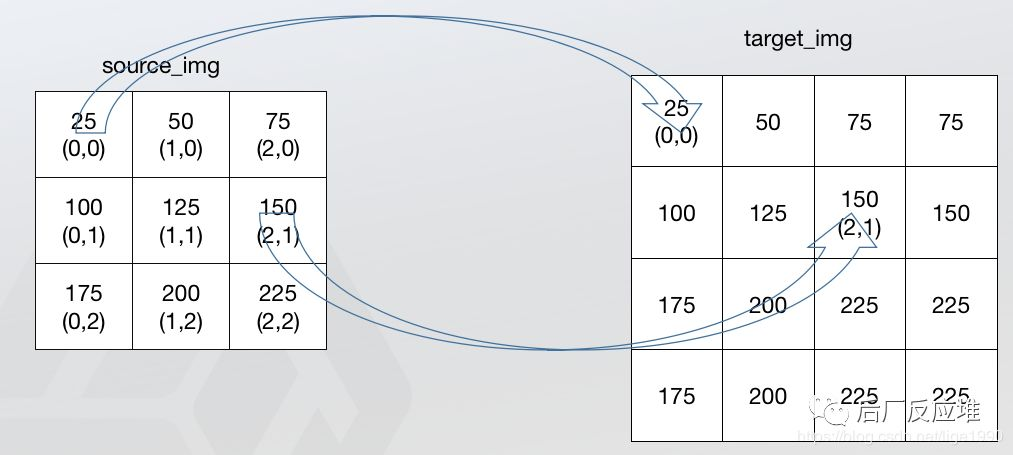
  上图效果是最近邻法的计算过程示意图，由上图可见，最近邻法只是把最外围的像素复制了一遍。最近邻法不需要计算只需要寻找原图中对应的点，所以最近邻法速度最快，但是会破坏原图像中像素的渐变关系，原图像中的值是渐变的，但是在新图像中局部破坏了这种渐变关系。

2.2 双线性插值对应的关系

  双线性插值的对应公式和前面的最近邻法一样，不一样的是根据对应关系不再是找最近的一个点，而是找最近的四个点，如下图所示：

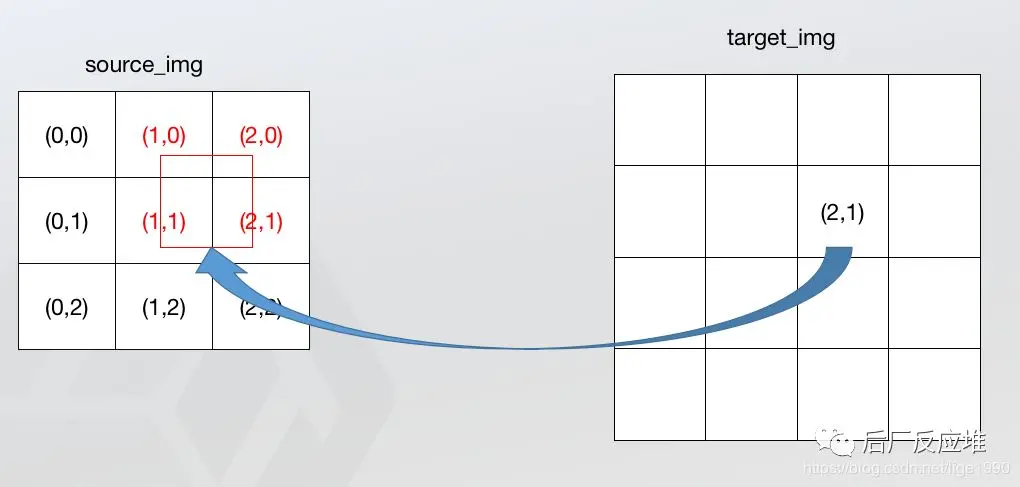
  这里我们根据四个点来计算一个点，这一个点是根据单线性插值在两个不同方向上计算出来的。下面先介绍以下单线性插值。

2.2.1 单线性插值

已知图像中P1和P2两个点，坐标分别为$(x1,y1)$、$(x2,y2)$，要计算$[x1,x2]$区间内某一位置x在直线上的y值。

  根据初中的知识，2点求一条直线公式（这是双线性插值所需要的唯一的基础公式）。
$$\frac{y-y_1}{x-x_1}=\frac{y_2-y_1}{x_2-x_1}\text{\hspace{1em}(1)}$$
  经过简单整理成下面的格式：
$$y=\frac{x_2-x}{x_2-x_1}{y}_1+\frac{x-x_1}{x_2-x_1}{y}_2\text{\hspace{1em}(2)}$$
  这里没有写成经典的AX+B的形式，因为这种形式从权重的角度很好理解。
  首先看分子，分子可以看成x与x1和x2的距离作为权重，这也是很好理解的，P点与P1、P2点符合线性变化的关系，所以P离P1近就更接近P1，离P2近就更接近P2。
  现在再把公式中的分式看作是一个整体，原式可以理解成y1和y2的加权系数，如何理解这个加权系数呢，要返回来思考一下，先明确根本目的：我们是要在图像中根据两个已知的像数值求未知点的像数值。这样一个公式是不满足写代码的需求的，图中的y1和y2分别代表原图像中的像素值，上面的公式可以写成如下格式。
$$f(P)=\frac{x_2-x}{x_2-x_1}f(P_1)+\frac{x-x_1}{x_2-x_1}f(P_2)\text{\hspace{1em}(3)}$$

2.2.2 双线性插值

  已知$Q_{11}(x_1,y_1)、Q_{12}(x_1,y_2)、Q_{2,1}(x_2,y_1)、Q_{22}(x_2,y_2)$，求其中$P(x,y)$的值。

  根据前面介绍的单线性插值，我们可以推算出双线性插值的计算过程，首先对$Q_{11}$和$Q_{21}$在X轴上求线性插值得到$R_1$，同样对$Q_{12}$和$Q_{22}$在X轴上求线性插值可以得到$R_2$，然后再对$R_1$和$R_2$在y轴上求线性插值得到$P_{(}x,y)$。
  1.x方向上的单线性插值，根据公式三有：
$$f(R_1)=\frac{x_2-x}{x_2-x_1}f(Q_{11})+\frac{x-x_1}{x_2-x_1}f(Q_{21})\text{\hspace{1em}(4)}$$
$$f(R_2)=\frac{x_2-x}{x_2-x_1}f(Q_{12})+\frac{x-x_1}{x_2-x_1}f(Q_{22})\text{\hspace{1em}(5)}$$
  2.y方向上的单线性插值，根据公式三有：
$$f(P)=\frac{y_2-y}{y_2-y_1}f(R_1)+\frac{y-y_1}{y_2-y_1}f(R_2)\text{\hspace{1em}(6)}$$
  将第一步结果带入第二步有
$$f(x,y)=\frac{f(Q_{11})}{(x_2-x_1)(y_2-y_1)}(x_2-x)(y_2-y)+\frac{f(Q_{21})}{(x_2-x_1)(y_2-y_1)}(x-x_1)(y_2-y)+\frac{f(Q_{12})}{(x_2-x_1)(y_2-y_1)}(x_2-x)(y-y_1)+\frac{f(Q_{22})}{(x_2-x_1)(y_2-y_1)}(x-x_1)(y-y_1)$$
  观察图片中双线性插值的关系图，可以有
$$x_2=x_1+1y_2=y_1+1\text{\hspace{1em}(8)}$$
  那么公式七中的分母全部为1，可以得到如下公式：
$$f(x,y)=f(Q_{11})(x_2-x)(y_2-y)+f(Q_{21})(x-x_1)(y_2-y)+f(Q_{12})(x_2-x)(y-y_1)+f(Q_{22})(x-x_1)(y-y_1)$$
  在有些资料中会写成权重的形式，上面的展开式是下面的权重表达式的正确求法：
$$f(x,y)=f(Q_{11})w_{11}+f(Q_{21})w_{21}+f(Q12)w_{12}+f(Q_{22})w_{22}\text{\hspace{1em}(10)}$$
  这种权重表达式也不难理解，观察一下可以发现每个点的权重都和代求点和对角点的距离有关。
  还有一个问题，当对应关系公式代入原图像中时，会与图像中的点发生重合，此时怎么选取剩下的三个点呢，根据公式十可以知道，无论我们选哪一个点，公式中其余的三点的权重会为0，所以无论我们选那个点，对最终的结果都不影响。
  至此，双线性插值的计算已经完成了，但是我们现在只能说勉强完成了双线性插值的算法。因为这种方式计算有较大的问题，至于问题可以看下面的内容。

2.2.3 双线性插值的优化

  原始公式的双线性插值之前的坐标$sr{c}_x,sr{c}_y$与插值之后的坐标$de{s}_x,de{s}_y$还有插值后的宽度与高度$de{s}_w,de{s}_h$和插值前的高度$sr{c}_w，sr{c}_h$，对应的原始的公式有：
$$sr{c}_x=\frac{de{s}_x\ast sr{c}_w}{de{s}_w}$$
$$sr{c}_y=\frac{de{s}_y\ast sr{c}_h}{de{s}_w}$$
  双线性插值的对应关系看似比较清晰，但是还是有两个问题，下面画图说明。
  根据坐标的不同，产生的结果不同，这张图是左上角为坐标原点的情况，我们可以发现最左边的都有几率直接复制到图像中。，而且就算不与图像的点重合，也相当于进行了一次线性插值。

  第二个问题是图像偏移的问题。假如一个3X3的图像插值成5X5的图像，原图像中心的位置原本是(1,1)，后面应该是(2,2)，可是根据公式计算的结果应该是(2,2)对应的(1.2,1.2)。插值后的图像发生了偏移。

  对此，坐标的对应关系可以做成中心对称的公式：
$$sr{c}_x=\frac{(de{s}_x+0.5)\ast sr{c}_w}{de{s}_w}-0.5$$
$$sr{c}_y=\frac{(de{s}_x+0.5)\ast sr{c}_h}{de{s}_h}-0.5$$
  将坐标带入可以发现（1，1）完美对应（2，2）。

双线性插值的直观感受

  上面通过公式说明了双线性插值是如何进行插值以及运算的。下面通过图形来直观感受一下线性插值的算法思想，这个有利于我们对后续MATLAB以及FPGA算法的实现。
  首先，有一副图像11x7如下：

  注意，这里交点代表像素，而不是方格。
  我们需要将他放大到19x12。放大后的图像大小如下图所示：

  然后将两幅图像缩放成同样大小然后进行重叠。

  橙色的部分点的像素信息（原图像）都是已知的，而我们就需要根据2.2.2以及2.2.3两个小节的公式根据橙色点的像素信息求出黑色点（缩放后的像素信息）。也就是根据重叠后黑色点最近的四个橙色点的加权和来得到黑色点的信息。

MATLAB实现双线性插值

clear;
clc;
close all;

src_data = double(imread('../img/640x480.bmp'));

[row,col] = size(src_data);

src_w = 640;
src_h = 480;

dst_w = 1280;
dst_h = 720 ;

line_data = zeros(dst_h,dst_w);

sx = src_w / dst_w;
sy = src_h / dst_h;
%先根据插值后的坐标求出插值前所需要的坐标
for i = 1:dst_h
    src_yf = ((i-1)+0.5) * sy - 0.5;%浮点数
    for j = 1:dst_w
        src_xf = ((j-1)+0.5) * sx - 0.5;%浮点数
        %得到附近四个点的坐标   x0 x1 y0 y1   需要求的点坐标xf yf
        if(src_xf<0)
            src_x0 = 0;
        else
            src_x0 = floor(src_xf);
        end

        src_x1 = src_x0 + 1;

        if(src_yf<0)
            src_y0 = 0;
        else 
            src_y0 = floor(src_yf);
        end

        src_y1 = src_y0 + 1;

        %根据四个点坐标以及待求点坐标计算出四个权重
        w11 = (src_x1 - src_xf) * (src_y1 - src_yf);   
        w21 = (src_xf - src_x0) * (src_y1 - src_yf);
        w12 = (src_x1 - src_xf) * (src_yf - src_y0);
        w22 = (src_xf - src_x0) * (src_yf - src_y0);
        %下面的+1是为了对应索引  与上面的+1求相邻坐标不一样
        if(src_y0 >= row - 1 && src_x0 >= col - 1)
            line_data(i,j) =    src_data(src_y0 + 1,src_x0 + 1) * w11;
        elseif(src_y0 >= row - 1)
            line_data(i,j) =    src_data(src_y0 + 1,src_x0 + 1) * w11 + ...
                                src_data(src_y0 + 1,src_x1 + 1) * w12;
        elseif(src_x0 >= col - 1)
            line_data(i,j) =    src_data(src_y0 + 1,src_x0 + 1) * w11 + ...
                                src_data(src_y1 + 1,src_x0 + 1) * w21;
        else
            line_data(i,j) =    src_data(src_y0 + 1,src_x0 + 1) * w11 + ...
                                src_data(src_y1 + 1,src_x0 + 1) * w21 + ...
                                src_data(src_y0 + 1,src_x1 + 1) * w12 + ...
                                src_data(src_y1 + 1,src_x1 + 1) * w22;
        end 
    end 
end 

dst_data = uint8(line_data);

subplot(1,2,1)
imshow(uint8(src_data));
subplot(1,2,2)
imshow(dst_data);