基于MATLAB的IIR滤波器设计与仿真

摘 要

随着社会的不断进步与发展，现代生活越来越趋向智能化，信号的收发与处理应用越来越广泛，但整个信号往
往不是我们所需要的，它除了包含我们所需要的信号成分外，还有其他频率的干扰无用信号成分，如果想要从中得
到我们所需要的一部分信号频率，我们就应该找一个类似于漏斗的东西把一些没用的信号过滤掉，这就需要滤波器
这一装置了。由于信号有数字和模拟信号之分，所以滤波器大致可以细分为数字和模拟两个方面。处理数字信号这
一方面的滤波器,顾名思义就是对数字进行运算处理的，这种滤波器具有很高的精度和良好的稳定程度，并且还不用
担心阻抗匹配的问题。从脉冲响应函数的时域特性的方面来说，数字滤波器又可以大致细分成无限长和有限长两类
方面，即人们通俗叫做IIR、FIR滤波器。其中脉冲响应是无限长的滤波器的可实现过程中所需要的阶数低，存储单
元少，并且它具有很高的效率，精度也高，除此之外还兼顾了模拟滤波器的一些相似之处。文中主要先简单说明了
滤波器及各种类型的概念以帮助理解，然后大致用脉冲响应不变法、双线性变换法还有一些直接或间接的方法在
MATLAB的基础上对巴特沃斯、椭圆等类型的滤波器进行了设计仿真。
关键词： MATLAB， IIR数字滤波器， 模拟滤波器

前 言

时代在不断发展，无论是军事还是日常生活中，滤波器问题都尤为重要。滤波器看名字就知道是滤波的装置，
更可以形象的把它想象为一个漏斗，这个“漏斗”可以使某些频率信号通过，但同时也会把其他一定频率的信号阻
挡掉，使之过不去。模拟滤波器由R、L、C三部分所构成，并且它还是一个连续信号系统；数字滤波器是离散时间系
统，由加法器、乘法器、存储器延迟单元、时钟发生器和逻辑单元组成，有很多优点：精度高、稳定性好、无阻抗
匹配问题、可以进行时分复用。
　　数字信号处理，顾名思义，就是研究以数字的方式来表示并处理信号波形，并且它的研究领域和范围很广。数
字滤波器根据不同的分类方式可以分成各种各样的滤波器，这些都在本文做详细阐述。数字滤波器与模拟滤波器相

比除了在数字信号处理具有一定的优势外，还具有很强的灵活程度、极高的稳定性、滤波器精度也高。

第1章 认识滤波器

1.1滤波器的定义
　　滤波器，是一种用于信号处理的“漏斗装置”，一整个信号相当于一杯浑水，滤波器可以把特定的某些频率相
当于清水过滤出来，而把其他的干扰杂质频率阻挡掉。
　　我们经常会看形形色色的信号波形图，图中信号幅度依然很高的说明通过了滤波器没有滤除掉，这些信号频率
所在的范围称为通带；而有些信号幅度大幅度衰减甚至几乎到0，这说明信号被抑制，这些信号所在频率的范围称为
阻带；通带与阻带之间的信号幅度突然大幅上升或下降，所在的频率称为截止频率。理想的情况下，滤波器通带上
的电压增益是一个不为零的常数，而阻带上的电压增益是0，但是在实际生活中，滤波器的通带和阻带之间是不会直
接相连接的，而是中间有一段过渡带在两者之间夹着。
1.2 滤波器的分类
从一个小角度来看：
A.可分成两类，处理的是模拟信号的为模拟滤波器，处理的是数字信号的为数字滤波器。
B.根据可以顺利通过滤波器而不被滤除抑制的信号频率的范围可分成：
低通滤波器：低频率或直流信号能够通过滤波器，而高频率信号基本被滤除掉。
高通滤波器：高频率信号能够通过滤波器，而低频率或直流信号基本被滤除掉。
带通滤波器：只有中间一段频率的信号通过，其他频率的信号基本被滤除，看起来像个凸起一样。
带阻滤波器：只有中间某一段频率的信号基本被滤除，其他频率的信号可以通过滤波器，看起来像个凹坑一样。
C.根据所用元件的不同，可分为：
无源滤波器：仅由无源元件（R、L和C）组成的滤波器。
有源滤波器：由无源元件（一般为R和C）和有源器件组成。[15]
　　D.根据冲激响应，数字滤波器分为IIR滤波器和FIR滤波器；IIR网络有反馈环，FIR网络没有反馈环。

第2章 滤波器的原理与设计

滤波器是对一个信号进行一系列处理的系统。滤波器还可以这样理解，按一定要求设计一个系统的频率响应，
然后这个系统会按照所设计的要求把信号的某些频率分量进行过滤、通过或抑制。
2.1 模拟滤波器的原理与设计
　　设计模拟滤波器的方法多种多样，其中我们可以用s域的系统函数
去逐步靠近所要设计的理想技术指标。
幅度平方函数在滤波器设计中起着至关重要的作用，一些特殊滤波器比如巴特沃思滤波器的设计公式都和它密不可
分。
　　在设计过程中，我们总想要结果趋近于理想，所以我们可以用幅度平方函数来表示理想的低通模拟滤波器的幅
度特性，即
（2.1）
由幅度平方函数确定
的方法是：
（a） 在
(b) 将
中，利用关系式
，得到
；
的有理式利用数学方法进行因式分解，找到其零点和极点。
© 根据具体情况，比较两个函数
和
的幅度特性，从而进一步确定增益常数。
　　从我们平时对模拟滤波器进行不断设计改造过程中，可以体会到低通滤波器往往是最容易设计的，但高通、带
通、带阻这三种滤波器在设计的时候就比较麻烦了。为了简便起见，我们可以利用容易设计的低通滤波器进行频带
变换，进而得到剩下的三种类型的滤波器。
2.2 数字滤波器的原理与设计
　　数字滤波器，即它的输入是数字信号，他的输出同样也是数字信号，并且经过滤波器后可以使输入信号的不同
频率分量的比例发生变化，也可以换一种理解方式，即可以使一部分信号分量通过滤波器，而另一部分信号分量得
到抑制或滤除。
　　能够顺利通过数字滤波器的频率范围不同，所划分的种类也不尽相同，共有低、高、带通滤波器外加一个带阻

滤波器。而从另一方面，即无论是看网络结构还是看单位脉冲响应，数字滤波器还可分为IIR滤波器和FIR滤波器两
种类型。可以用n阶差分方程把IIR滤波器表示出来：
（2.2）
或用它的Z域系统函数:
（2.3）
对照模拟滤波器的传递函数:
（2.4）
　　可总结出,数字滤波器与模拟滤波器，它们二者之间的设计的大致思路差不多,主要采用了逼近的思想来达到所
设计的指标，这一思想所采用的是寻找一组合适的系数的方法；但是二者之间也有所不同之处，就是各自在各自的
频域寻找适合的系统函数，像数字滤波器是在Z域, 而模拟滤波器则是在S域。由此看来，数字和模拟之间相互联
系、相辅相成，所以我们可以考虑用模拟滤波器系统函数的一些成熟的设计来针对数字滤波器设计它的系统函数H
(Z),简单来说就是把模拟滤波器进行离散化处理。

第3章 IIR数字滤波器的设计

3.1 IIR数字滤波器简介
　　数字滤波器属于一个离散域的线性时不变系统，它可以对采样来的信号进行一些公式上、数学上的运算或转
化，进而进行滤波过程。数字滤波器的输入、输出两个端口都是不连续的数字量。因为IIR滤波器属于离散域，所以
它的计算和滤波经常采用差分方程来运算。模拟滤波器转换成数字滤波器的方法主要有两种：一个是脉冲响应不变
法，另一个是双线性变换法，所以IIR数字滤波器可以通过这两种方法来设计。其中模拟滤波器有不少优点：设计简
单方便，有许多图表可供参考。
3.2 IIR数字滤波器的特点
IIR数字滤波器有以下四类特点：
（1）系统函数通过一系列数学公式转化，能以封闭函数的式子呈现。
　　（2）采用的是具有反馈环路的递归型结构。一些基本的运算模块，诸如延时模块、相加相乘模块等等，它们之
间相互组合搭配，形成级、并联等四种IIR滤波器的运算结构形式
　　（3）如今模拟滤波器的理论已经十分成熟，具有大量可查阅图表，并且具有巴特沃斯、切比雪夫等已经成型的
滤波器技术，这些滤波器具有数不胜数的优点，大大减少了我们的工作量。所以我们可以产生数字滤波器设计的一
个新思路，就是把模拟滤波器的一些公式通过一些变换进行转化。
（4）它的相位特性没有一定的规律，也不太容易控制，有时要加一个用于相位校准的网络提高准确性。
3.3 IIR数字滤波器的主要技术指标
数字滤波器的主要技术指标为：
(1) 特征频率参数
滤波器的频率参数主要有：
①通带截止频率
②阻带截频
：为通带与过渡带相交界的频率。
：为阻带与过渡带相交界的频率。
③转折频率
：为信号功率衰减到
时的频率。
④当电路没有损耗时，固有频率
(2) 增益和衰减[1]
，也就是其产生谐振时的频率。
　　滤波器在信号可通过的频率范围内的增益并不是一个固定的量，不同类型的增益。①对于低通而言，通频带的
增益 一般指
时所产生的增益；对于高通而言，通频带的增益 指
时所产生的增益；对于带通而
言，通频带的增益 则指信号处于中心频率时所产生的增益。②对带阻而言，不应该关注增益而更应该关注衰减，

二者互为倒数。③通频带增益的变化量 指通带内各点增益的最大变化量，如果 以为单位，则指增益
值的变化量。
(3) 阻尼系数与品质因数
　　阻尼系数是表示滤波器对角频率为信号起到阻尼作用的一项测量指标，注意这一系数是用来表示能量衰减
的，而不是增益。阻尼系数与品质因数互为倒数关系，即Q=1/，其中品质因数与带通、带阻滤波器选择信号的频
率的性质有关系。
(4) 灵敏度
当滤波器的某一个性能指标对另一个性能指标变化的灵敏度记为，定义为：
(3.1)
　　灵敏度也是滤波器设计过程中必不可少的一个参数，它和电路容错能力有一定的联系，即灵敏度越小，相应的
电路容错能力越大，随之稳定性就越高。
(5) 群延时函数[2]
　　信号经过滤波器的处理后，难免会产生一些失真，这一程度一般用一种函数来衡量，即群延时函数
，式子中有这样一种关系： 越接近常数，信号相位的失真越小。
3.4 IIR数字滤波器的设计
　　其设计方法可以分为两种：一个是先把模拟滤波器设计出来，通过某些运算关系来设计出数字滤波器；而另一
种则是通过设计一个过渡作用的模拟滤波器得到系统函数
，再通过某种方法把
转换成数字滤波器的系
统函数
。为了保证转换后的
是稳定的，即极点在单位圆内，并且满足我们所需要的一些指标，所以我们
对两者之间的转换关系做出了两点要求:
（1）模拟滤波器转换成数字滤波器，前者是因果稳定的，则后者同样也是因果稳定的系统。
（2）两者的频率响应之间有一定的线性对应关系，如s域的虚轴映射为z域的单位圆。
利用模拟滤波器的设计过程是：
(1)确定数字低通滤波器的技术指标：通带边界频率 、通带最大衰减 、阻带截止频率 、阻带最小衰减 。
(2)把数字低通滤波器的技术指标转换成相对应的模拟低通滤波器的技术指标。[13]
(3)按照模拟低通滤波器的技术指标设计过渡模拟低通滤波器。[14]
(4)用所选的转换方法，将模拟滤波器的系统函数
3.4.1脉冲响应不变法设计IIR数字滤波器
一 设计原理
转换成数字低通滤波器的系统函数
。
　　模拟滤波器的系统函数为
，它的单位冲激响应是
，
是
的拉普拉斯变换。数字滤波器的
。脉冲响应不变法实质上是一种在
系统函数
　　对
与
是一组Z变换对的关系。
进行等间隔的信号采样，其中采样的间隔为T，这样可以得到

作为数字滤波器的单位脉冲响应，它使
在采样点上等于
。因为我们
一开始设计的模拟滤波器的设计结果是
，而我们最终需要设计的是
，所以我们需要两者之间的转换：
利用采样的数字信号序列的Z变换与模拟信号的拉氏变换的关系得到
(3.2)
可知此法将S域通过运算变换成了Z域，
两个域之间的标准变换关系式
。

由（3.2）式，数字、模拟滤波器两者之间的频响有着运算关系，即
(3.3)
　　可以从中看出，数字与模拟滤波器频响之间的关系是：前者是后者的周期延拓。只有当模拟滤波器的频响是限
带的，并且带限于折叠的频率范围以内时，即
(3.4)
才会使数字滤波器的频响不产生混叠失真的现象，即
(3.5)
　　但是在实际生活中，总有一些方面是不理想的，比如：不是严格限带的，会生频谱混叠失真现象等等。不过从
整体来看，采用脉冲响应不变法来设计数字滤波器的效果还是可以的。
　　对模拟滤波器的单位冲激响应
按照一定的采样频率进行采样，若提高采样频率，使得系统频率响应各周期
延拓分量之间的距离更远，从而大大防范了频谱混叠这种现象的产生。
二 脉冲响应不变法的优缺点
优点：一方面是此法的时域逼近性良好，另一方面是模拟频率 和数字频率 两者之间具有
缺点：频率响应会产生频谱混叠失真的现象。
3.4.2双线性变换法设计IIR数字滤波器
的线性关系。
一 设计原理
　　双线性变换法是采用正切变换来实现非线性频率压缩。先将S域变换到一个过度域，即S1域(
～ 之间)，
再利用关系式
转换到Z域。这样就使S域与Z域建立了单值对应的关系，消除了频谱混叠失真的现象。
为了将S域的整个虚轴 压缩到S1域
(3.6)
1轴上的
到
段上，可以通过下面正切变换的运算公式来实现
当Ω1由 变化到时，对应的Ω由 变化到 ，也即映射了整个 轴。将式（3.6）写成
(3.7)
令=S，1=S1，则得
(3.8)
再将S1平面通过以下标准变换关系映射到Z平面
(3.9)
从而得到S平面和Z平面的单值映射关系为：
(3.10)

(3.11)
　　式（3.10）与式（3.11）表示的是S域与Z域之间具有一对一单值映射的关系，此法顾名思义，其变换表示的是
两个线性函数之比。
二 双线性变换法的优缺点
　　主要的优点是避免了滤波器频率响应所产生的混叠现象。这种方法可由简单的代数公式直接将
转换成
，工程实际中设计非常容易。缺点是当阶数稍高时，将
整理的工作就会变困难。

第4章 IIR滤波器的实现

4.1 利用模拟滤波器设计IIR数字滤波器
一般步骤如下:
（1）将所要设计的数字滤波器的技术指标按一定关系转换成模拟低通滤波器的技术指标；[9]
（2）根据转换后的技术指标,通过滤波器阶数选择函数，从而确定最小阶数N和固有频率Wn；
（3）运用最小阶数N产生模拟滤波器[12]；
（4）运用固有频率Wn把模拟低通滤波器转换成模拟低通、高通、带通、带阻滤波器；[10]
（5）运用冲激响应不变法或双线性变换法把模拟滤波器转换成数字滤波器。[11]
4.1.1 巴特沃斯和椭圆数字低通滤波器的设计
A.巴特沃斯低通滤波器[3]
　　我们可以规定它的一些技术指标：通频带的边界频率为3kHZ，通频带的最大衰减为1dB；阻带的边界频率为
10kHZ，阻带的最小衰减为40dB,信号采样的频率为20kHZ。
其幅度平方函数为
（4.1）
其系统函数为
（4.2）
低通巴特沃斯滤波器设计步骤如下：
（1）确定阶数N。
（2）求极点
归一化低通原型系统函数为
归一化低通滤波器系统函数为
（3）将
去归一化最终得到
用脉冲响应不变法设计的的程序如下：
fp=3000;

fs=10000;
Fs=20000;
Rp=1;
Rs=40;
T=1/Fs;
W1p=fp/Fs2;W1s=fs/Fs2;
[N,Wn]=buttord(W1p,W1s,Rp,Rs,‘s’);
[z,p,k]=buttap(N);
[bp,ap]=zp2tf(z,p,k);
[bs,as]=lp2lp(bp,ap,WnpiFs);
[bz,az]=impinvar(bs,as,Fs);
sys=tf(bz,az,T);
[H,W]=freqz(bz,az,512,Fs);
subplot(2,1,1);
plot(W
gridon;
xlabe
ylabe
,20*log10(abs(H)));
l(‘频率/Hz’);
l(‘振幅/dB’);
subplot(2,1,2);
plot(W,abs(H));gridon;
xlabel(‘频率/Hz’);
ylabel(‘振幅/H’);
运行后的波形如下：

图4.1 巴特沃斯滤波器在Matlab上运行波形
从波形图中可以看出，滤波器设计指标都达到要求。
B椭圆低通滤波器
　　我们可以规定它的一些技术指标：通频带的边界频率为3kHZ
，阻带的最小衰减40dB,信号的采样频率为20kHZ。
它的幅度平方函数[4]为：
，通频带的最大衰减为1dB；阻带的边界频率为
9kHZ

(4.3)
双线性变换法设计步骤如下：
（1）写出滤波器的系统函数
（2）利用双线性变换法得到的系统函数
为
其用双线性变换法设计的程序如下：
fs=20000;
wp=2pi3000/fs;
ws=2pi9000/fs;
Rp=1;
Rs=40;
Ts=1/fs;
Wp=2/Tstan(wp/2);Ws=2/Tstan(ws/2);
[N,Wn]
[z,p,k]
[Bap,Aap]=zp2tf(z
[b,a]
[bz,az]
[H,f]=freqz(bz,az,512,fs);
=ellipord(Wp,Ws,Rp,Rs,‘s’);
=ellipap(N,Rp,Rs);
,p,k);
=lp2lp(Bap,A
ap,Wn);
=bilinear(b,a,fs);
subplot(2,1,1);
plot(f,20*log10(abs(H)));
title(‘N=2时产生的频率响应’);
gridon;
xlabel(‘频率/Hz’);
ylabel(‘振幅/dB’);
subplot(2,1,2);
plot(f,abs(H));gridon;
xlabel(‘频率/Hz’);
ylabel(‘振幅/H’);

可以看出，设计出来的滤波器符合预期设计要求。
4.1.2 切比雪夫数字滤波器的设计
　　从幅度谱形成的规律和总结出的性质上来看，Ⅰ型在信号顺利通过滤波器的频率范围内是等波纹的，在信号被
抑制的频率范围内是单调的，而Ⅱ型却是恰恰相反。
Ⅰ型的幅度平方函数为：
下面我们举一些实例
　　A、本例子运用函数cheblap为基础设计Ⅰ型滤波器。我们规定的一些参考指标为：通频带信号的截止频率为
8000rad/s，通频带信号的最大衰减为4dB，阻频带信号的截止频率为30000rad/s，阻频带信号的最小衰减为40dB。
程序如下：
a=8000;b=30000;AP=4;AS=40;
T1=sqrt(10^(0.1AP)-1);
T2=sqrt(10^(0.1AS)-1);
N=ceil(acosh(T2/T1)/acosh(b/a));
[Z,P,K]=cheb1ap(N,AP);
　　syms rad; hs1=K/(irad-P(1))/(irad-P(2))/(irad-P(3));
hs2=10log10((abs(hs1))^2);
ezplot(hs2,[-15,15]);
grid on;
仿真图形如图4-4所示：

图4.3 切比雪夫Ⅰ型带通滤波器响应曲线
　　B、首先我们已经了解了I型滤波器的设计，即以cheby1函数为基础设计出低通型，其他诸如高通、带通型的可
以在此基础上进行变换得到。以cheby2 函数为基础设计各种II型滤波器可以类比于I型，唯一不同的点是cheby2 设
计出的滤波器在带阻是等波纹的，在带通是单调的，而cheby1是与之相反的。
　　我们要设计一个低通切比雪夫II 型数字滤波器，其中设计参数包括：阶数为10 ，通频带的截止频率为350
Hz，信号的采样频率为1000 Hz ，带阻的波纹为30 db，程序如下：
[b,a]=cheby2(10,30,350/500);
freqz(b,a,512,1000);

我们要设计一个低通cheby1 数字滤波器，设计的参考指标是：阶数为10、通频带的截止频率为350 Hz ，信号
的采样频率为1000 Hz ，通频带的波纹为30db，程序如下：
[b,a]=cheby1(10,30,350/500);
freqz(b,a,512,1000);
仿真图形如图4.5所示：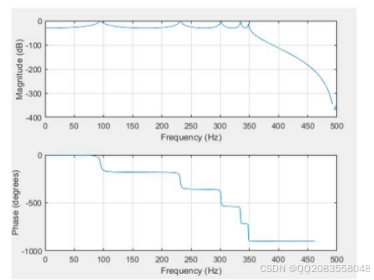

图4.5 切比雪夫低通I 数字滤波器
由仿真图像可以看出，技术指标都基本达到我们所设计的初始要求，设计成功。

4.2 IIR数字滤波器的直接设计法
直接设计法，也就是直接调用MATLAB信号处理工具箱提供的函数来设计，主要有以下方法：
1.零极点累试法
在确定零极点位置时要注意：
(1)为保证数字滤波器是一个因果、稳定系统，极点必须位于z平面单位圆内。
(2)为保证系统函数写成有理式时的系数是实数，复数零极点必须形成一组共轭对。[5]
2.在频域利用幅度平方误差最小法直接设计IIR数字滤波器[6]
3.在时域直接设计IIR数字滤波器[7]
　　我们要设计设计两个参数完全一样的数字低通滤波器，一个是I型，另一个是II
频带的边界频率为2kHZ，通频带的最大衰减为1dB；阻带的边界频率为9kHZ，阻带的最小衰减为40dB,信号的采样频
率为19kHZ。
型，它们共同的参数指标是：通
切比雪夫I型的程序如下：
Fs=19000;
Flp=2000;
Fls=9000;
Wp=2Flp/Fs;
Ws=2Fls/Fs;
Rp=1;
Rs=40;
[N,Wn]=cheb1ord(Wp,Ws,Rp,Rs);
[b,a]=cheby1(N,Rp,Wn);
[hw,w]=freqz(b,a);
subplot(2,1,1);
plot(w/pi,20*log10(abs(hw)));gridon;
xlabel(‘ω/π’);ylabel(‘幅度（dB）’)
title(‘切比雪夫I型幅频响应’);
subplot(2,1,2);plot(w/pi,abs(hw));
gridon;
xlabel(‘ω/π’);ylabel(‘幅度（H）’);
运行后的波形如下：

图4.6 切比雪夫 I型运行波形
切比雪夫II型M程序如下：
Fs=19000;
Flp=2000;
Fls=9000;
Wp=2Flp/Fs;
Ws=2Fls/Fs;
Rp=1;
Rs=40;
[N,Wn]=cheb2ord(Wp,Ws,Rp,Rs);
[b,a]=cheby2(N,Rs,Wn);
[hw,w]=freqz(b,a);
subplot(2,1,1);
plot(w/pi,20*log10(abs(hw)));grid on;
xlabel(‘ω/π’);ylabel(‘幅度（dB）’)
title(‘切比雪夫II型滤波器的幅频响应’);
subplot(2,1,2);plot(w/pi,abs(hw));
grid on;
xlabel(‘ω/π’);ylabel(‘幅度（H）’);
运行后的波形：

图4.7 切比雪夫 II型运行波形
　　从幅度频谱图中可以看出:巴特沃斯滤波器的幅度一直保持逐渐下降的趋势，在通频带内的曲线比较平滑;切比
雪夫I型滤波器在通频带范围内幅度有波动，而阻带内幅度呈现单调的趋势;而II型与I型性质相反。[8]

第5章 IIR数字滤波器的综合设计和仿真

因为Matlab软件中信号处理工具箱中有大量现成的可使用的滤波函数，所以用基于Matlab的直接变换方法设计
IIR数字滤波器是非常简便的。本文主要以切比雪夫I型函数的例子进行了设计。

5.1 数字低通滤波器设计实例与仿真
　　设计一个cheby1 数字低通滤波器，其中我们规定的一些参数指标为：对信号进行采样的频率为1000 Hz ，阶次
为10阶、截止频率为100 Hz，在带通的波纹为1dB. 滤波的结果图如图5.1.2，图5.1.3所示。
其设计程序如下：
%切比雪夫Ⅰ型数字低通通滤波器直接设计
f0=1000 [b,a]=cheby1(10,1,100/500);
freqz(b,a,512,1000);
figure(1)
n=0:500;t=n/f0;
f= cos(2pit40)+sin(2pit75)+sin(2pit*100);
figure(2)
subplot(4,1,2);plot(f);
axis([0,200,-5,5]);
grid on;
xlabel(‘图5.1.2 原始信号波形’);
y1=filter(b,a,f);
subplot(4,1,3);plot(y1)
axis([0,200,-5,5]);
grid on;
xlabel(‘图5.1.3 滤波后的信号波形’);

图5.1 运行波形
由运行出来的波形图可以形象看出，此滤波器从幅频和特性这两个方面的特性，都是满足一开始设计要求的指标。
滤波效果见下图：

图5.2 仿真图形
　　仿真结果显示，干扰后的混合信号是具有40Hz、75Hz和100Hz这三种频率的信号相互融合在一起传输的波形信
号，而我们所需要的只是40Hz的频率信号，可以看出这一频率的信号已经被或高或低的频率信号的混杂和干扰，这
时滤波器就起到了至关重要的作用。经过滤波器滤波之后的所输出信号可以算出正好是40Hz频率的信号。
5.2 数字带通滤波器设计实例与仿真
　　我们要设计一个cheby1 数字带通滤波器，规划的一些重要参数：通带内的截止频率是wp1＝300Hz，
wp2＝800Hz，阻带内的截止频率是：ws1＝200Hz，ws2＝900Hz；阻带内的最大衰减为4dB，阻带内的最小衰减为
30dB；对信号的抽样频率为10000Hz。进行滤波的结果图如图5.2。
MATLAB具体程序如下：
fp=[300,800];
fs=[200,900];
f0=10000;
wp=2pifp/f0;
ws=2pifs/f0;
rp=4;
rs=30; [n,wn]=cheb1ord(wp/pi,ws/pi,rp,rs);
[b,a]=cheby1(n,rp,wn);
[h,w]=freqz(b,a,128,10000);
mag=abs(h);pha=unwrap(angle(h));
subplot(3,1,1);plot(w,mag);
axis([0,1000,0,1]);
grid on;
xlabel(‘图5.2.1 切比雪夫Ⅰ型带通滤波器所产生的频率响应曲线’);
n=0:500;t=n/f0;
x1=2sin(2pi500t)+randn(size(t)) ;
subplot(3,1,2);plot(x1);
axis([0,300,-5,5]);
grid on;
xlabel(‘图5.2.2 带有噪音的500Hz正弦波波形’);
y1=filter(b,a,x1);
subplot(3,1,3);plot(y1);
axis([0,300,-5,5]);
grid on;

由图5.2.1可以看出，设计出的切比雪夫带通滤波器基本符合所规划的参数指标。
　　由图5.2.2、5.2.3可以看出，一个信号经过被白噪声污染之后，以输入信号的方式通过此滤波器后，白噪声这
种“杂质”会被顺利滤除掉，剩下的是我们所需要的信号，同时滤波器还提高信号的信噪比，完成了我们所需要的
参数指标。

总 结

本文如课题所写，主要介绍了基于MATLAB的IIR数字滤波器的设计与应用,从文首到文末，有两个方法使我印象
深刻，其中一个是脉冲响应不变法，另一个是双线性变换法。脉冲响应不变法不仅设计起来简单方便，还有一些优
点：相位响应有着很好的线性关系,并且不会有有关稳定的一些问题，但可能会产生频谱混叠，而相比之下双线性变
换法正好避免了这种现象。还有一种主要经典的设计滤波器的思路，那就是可以利用模拟滤波器进行过度，通过一
些数学上的运算转换，从而设计出数字滤波器。除了这种典型设计思路以外，MATLAB软件中的信号处理工具箱还有
一些可以直接调用的成熟函数，所以我们可以直接编程调用这些函数来直接设计IIR滤波器。
　　 此次对毕业论文的撰写和设计，使我加深了对论文的格式的认知和撰写流程的熟悉，不仅是对我自身一些方面
能力的提升，而且加深了我对信号处理及滤波器设计的理解与应用。此次设计还用到了MATLAB仿真，提高了我的逻
辑思维能力和编码能力。另外，自己的专业素养和动手操作能力有所提升。相信这些能给我带来很大的帮助，并能
促进我今后的科研工作学习。

谢 辞

论文完成的过程，不仅一次艰辛的过程，更是一次促进自己成长的历练。在实验操作与论文撰写中，我要感谢
我的老师董淑敏老师。董淑敏老师不仅在学习、生活上对我非常关怀，并对我的论文工作关怀备至。她严谨的科学
态度，积极向上的治学精神，使我深受感触，并深深影响着我，是我重要的人生导师。在此向董老师致以诚挚的谢
意。
我还要感谢在写毕业论文过程中帮助过我的同学，我们之间相互鼓励，遇到难题一起想办法，使得论文圆满完成。