随机变量及其分布

最新推荐文章于 2024-07-23 22:59:42 发布

q_1703

最新推荐文章于 2024-07-23 22:59:42 发布

阅读量1.2k

点赞数 17

文章标签：概率论

本文链接：https://blog.csdn.net/q_1703/article/details/137428187

版权

一、定义

设E是随机试验，它的样本空间是S={e}.如果对于每一个e∈S，有一个实数X(e)与之对应，这样就得到一个定义在S上的单值实值函数X(e),称X(e)为随机变量.可简写为随机变量X.

1）随机变量与普通的函数不同

2）随机变量的取值具有一定的概率规律

二、分类

1)离散型：随机变量所取的可能值是有限多个或无限可列个

2)连续型：随机变量所取的可能值可以连续地充满某个区间

比如“灯泡的寿命”，X的取值范围为[0,+∞].

一）离散型随机变量的分布律

1.两点分布，b(1,p)

设随机变量X只可能取0与1两个值，它的分布律为

X	0	1
P	1-p	p

或记为 $P(X = k) = {(1-p)}^{1-k}p^k,k = 0,1$

则称X服从（0-1）分布或两点分布，一般用符号X~b(1,p)表示.

2.伯努利试验、二项分布

试验是相互独立的

n重伯努利试验实验

设试验E只有两个可能结果，A及非A，则称E为伯努利试验.

如果独立重复进行n次

$P(X = k) =\binom{n}{k}p^kq^{n-k},k = 0,1,2,...,n.$

称随机变量X服从参数为n，p的二项分布，并记为X~b(n,p)

特别，当n =1 时二项分布化为

$P(X = k) = {(1-p)}^{1-k}p^k,k = 0,1$

这是（0-1）分布.

3.泊松分布 Π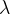（ $\lambda$ ）

当二项分布X~b(n,p)中n>10,p<0.1时，则逼近泊松分布

设随机变量X所有可能取的值为0,1,2,...，而取各个值的概率为

$P(X=k) = \frac{\lambda ^{k}e^{-\lambda }}{k!},k = 0,1,2,...,$

其中 $\lambda$ >0是常数，则称X服从参数为 $\lambda$ 的泊松分布，记为X~Π( $\lambda$ ).

ps: $\lambda$ = np

二）连续型随机变量及其概率密度

$F(x) =\int_{-\infty}^xf(t)dt$

F(x)是分布函数，f(x)是概率密度.

1.均匀分布

设连续型随机变量X具有概率密度

$f(x) = \left\{\begin{matrix} \frac{1}{b-a},a<x<b,\\ 0,else, \end{matrix}\right.$

则称X在区间（a,b)区间上服从均匀分布，记为X~U(a,b).

分布函数为

$f(x) = \left\{\begin{matrix} 0,x<a,\\\frac{x-a}{b-a},a\leq x<b,\\ 1,x\geq b, \end{matrix}\right.$

2.指数分布

设连续型随机变量X具有概率密度

$f(x) = \left\{\begin{matrix} \frac{1}{\Theta }e^{-\frac{x}{\Theta }},0<x,\\ 0,x\leq 0, \end{matrix}\right.$

其中 $\Theta$ >0为常数，则称X服从参数为 $\Theta$ 的指数分布.

分布函数为

$f(x) = \left\{\begin{matrix} 1-\frac{1}{\Theta }e^{-\frac{x}{\Theta }},0<x,\\ 0,x\leq 0, \end{matrix}\right.$

3.正态分布（或高斯分布）

设连续型随机变量X的概率密度为

$F(x) = \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}},-\infty<x<+\infty$

其中 $\mu$ ， $\sigma$ （ $\sigma$ >0）为常数，则则称X服从参数为 $\mu$ ， $\sigma$ 的正态分布或高斯分布.记为X~N( $\mu$ , $\sigma ^2$ ).

1)曲线关于x = $\mu$ 对称；

2)当 x = $\mu$ ,f(x)取得最大值 $\frac{1}{\sqrt{2\pi}\sigma}$ ；

3）当x趋于无穷时，f(x)趋于0；

4）曲线在x = $\mu$ ± $\sigma$ 处有拐点;

5)曲线以x轴为渐近线.

分布函数为

$F(x) = \frac{1}{\sqrt{2\pi}\sigma} \int_{-\infty}^xe^{-\frac{(t-\mu)^2}{2\sigma^2}}dt$

三、分布函数

定义：设X是一个随机变量，x是任意实数，函数F(x) = P{X<=k}称为X的分布函数

离散型随机变量分布律与分布函数的关系

分布律： $p_{k} = P \{X = x_{k}\}$

分布函数： $F(x) = P\{X\leq x\} = \sum_{x_{k} \leq x}{p_{k}}$

离散型：阶梯型

连续性：连续

q_1703

关注

17
点赞
踩
13

收藏

觉得还不错? 一键收藏
1
评论
复制链接

分享到 QQ

分享到新浪微博

扫一扫

随机变量及其分布

一、定义

二、分类

一）离散型随机变量的分布律

1.两点分布，b(1,p)

2.伯努利试验、二项分布

3.泊松分布 Π（）

二）连续型随机变量及其概率密度

1.均匀分布

2.指数分布

3.正态分布（或高斯分布）

三、分布函数

3.泊松分布 Π（ $\lambda$ ）