算法模型---回归模型

本文参考线性回归之最小二乘法及线性回归浅谈

线性回归模型与最小二乘法

1、基本概念

线性回归假设因变量与自变量之间存在线性关系，因变量可通过自变量线性叠加而得到，即因变量和自变量之间可用如下方式表示。

$$y=w_0+w_1x_1+w_2x_2+...+w_nx_n$$

式中${x_1,...,x_n}$为自变量，${w_1,...,w_n}$为权重系数，$w_0$为偏置。
线性回归就是要解决如何利用样本求取${w_1,...,w_n}$和$w_0$，拟合出上述表达式，获得最佳直线的问题。最常用的就是最小二乘法。
最小二乘法：最佳拟合线下，将已知样本的自变量代入拟合直线，得到的观测值与实际值之间的误差平方和最小。

2、一元线性回归

为了好理解，先从简单的情况开始，即一元线性回归。

2.1、利用方程组来解系数

假设因变量和自变量可用如下函数表示：
$y=ax+b$对于任意样本点$(x_i,y_i)$,有误差$e=ax_i+b-y_i$，误差平方和$\sum_1^ne^2=\sum_1^n(ax_i+b-y_i)^2$
那什么样的a和b会使得误差平方和最小呢？
上面是求最值的问题，我们会想到导数和偏导数，这里在偏导数等于0的地方能取到极值，并且也是最值。
分别对a和b求偏导得到如下表达式：

$$\begin{align} \frac{\partial}{\partial a} &=\sum_{i=1}^n2x_i(ax_i+b-y_i) \\ \frac{\partial}{\partial b} &=\sum_{i=1}^n2(ax_i+b-y_i) \end{align}$$
通过对二元一次方程组
$$\begin{align} \sum_{i=1}^n2x_i(ax_i+b-y_i)&=0 \\ \sum_{i=1}^n2(ax_i+b-y_i)&=0 \end{align}$$
进行求解，可以得到如下解：
$$\begin{align} a&=\frac{n\sum_{i=1}^n x_i y_i-\sum_{i=1}^n x_i \sum_{i=1}^n y_i}{n\sum_{i=1}^n x_i^2-(\sum_{i=1}^n x_i)^2} \\ b&=\frac{\sum_{i=1}^n x_i^2\sum y_i-\sum_{i=1}^n x_i \sum_{i=1}^n x_i y_i}{n\sum_{i=1}^n x_i^2 -(\sum_{i=1}^n x_i )^2} \end{align}$$
上面的数学过程用代码表示如下：

import numpy as np
import matplotlib.pyplot as plt

def calcAB(x,y):
    n = len(x)
    sumX, sumY, sumXY, sumXX = 0, 0, 0, 0
    for i in range(0, n):
        sumX += x[i]
        sumY += y[i]
        sumXX += x[i] * x[i]
        sumXY += x[i] * y[i]
    a = (n * sumXY - sumX * sumY) / (n * sumXX - sumX * sumX)
    b = (sumXX * sumY - sumX * sumXY) / (n * sumXX - sumX * sumX)
    return a, b
xi = [1,2,3,4,5,6,7,8,9,10]
yi = [10,11.5,12,13,14.5,15.5,16.8,17.3,18,18.7]
a,b=calcAB(xi,yi)
print("y = %10.5fx + %10.5f" %(a,b))
x = np.linspace(0,10)
y = a * x + b
plt.plot(x,y)
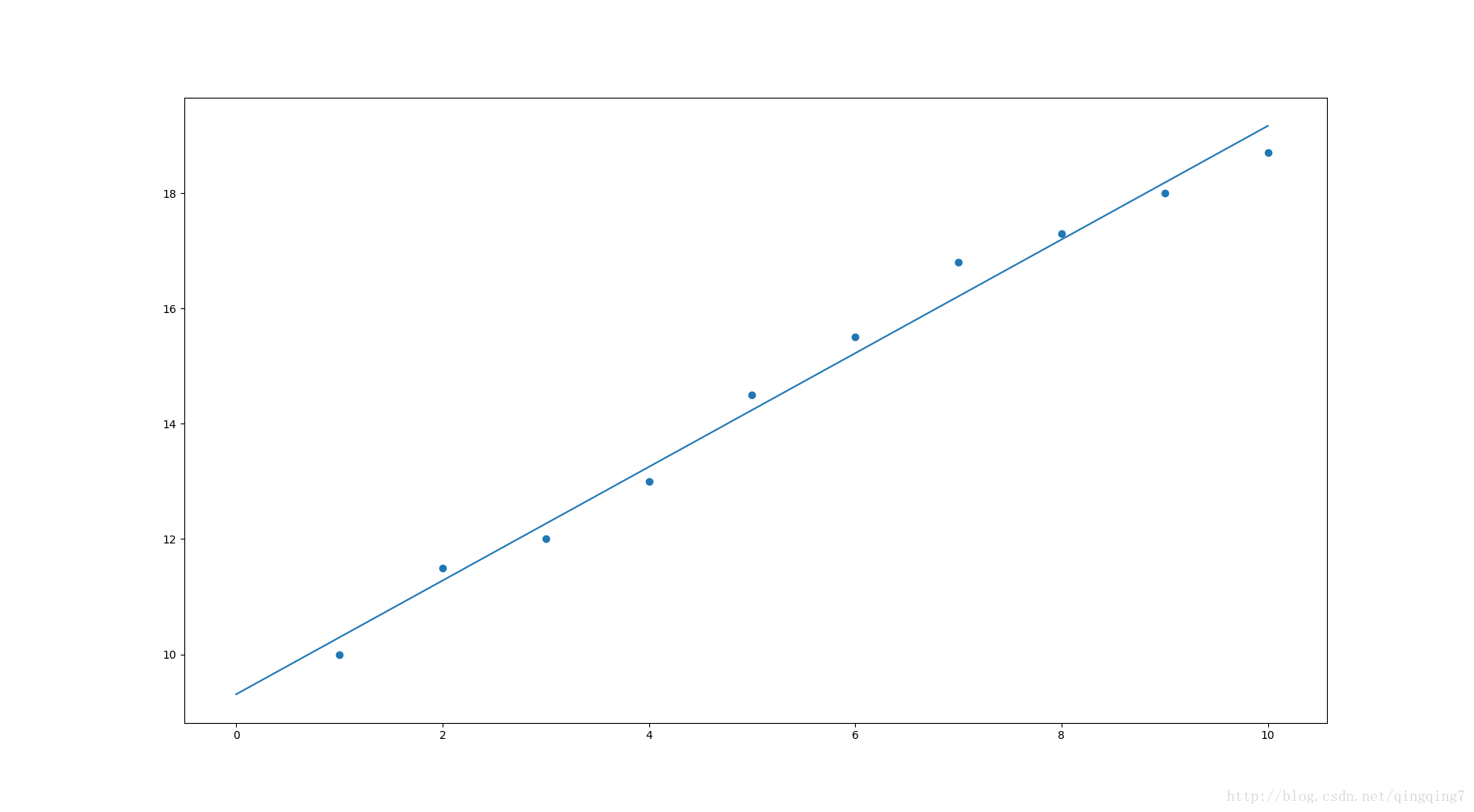
plt.scatter(xi,yi)
plt.show()

数据散点和拟合的直线如下：

2.2、利用矩阵的方法来求解系数

函数$y=ax+b$
也可以表示成如下的形式
$y=w_0+w_1 x=W^T x=(xW)^T$

式中$W=[w_0,w_1]^T,x=[1,x_i]^T$

对于n个样本，此时损失函数（即误差平方和）为：

$$L=\sum_{i=1}^n (y_i-W^T x_i)^2$$

假如我们将样本表示成如下形式：

$$Y=[y_1,y_2,...,y_n]^T$$
$$X=\left[ \begin{matrix} 1,x_1\\1,x_2\\...\\1,x_n\\ \end{matrix} \right]$$
则
$$\begin{align} Y-XW&=\left[ \begin{matrix}y_1-(w_0+w_1x_1)\\y_2-(w_0+w_1x_1)\\...\\y_n-(w_0+w_1x_n)\end{matrix}\right] \\ (Y-XW)^T&=[y_1-(w_0+w_1x_1),y_2-(w_0+w_1x_1),...,y_n(w_0+w_1x_n)] \\ (Y-XW)^T(Y-XW)&=\sum_{i=1}^n (y_i-W^T X_i)^2 \\ &=L \end{align}$$
进一步，可以将损失函数表示如下形式：
$$L=Y^TY-w^TY-Y^XW+W^TX^TXW$$
L对W求导，可得到
$$\frac{\alpha L}{\alpha w}=-2Y^TX+2W^TX^TX$$
令导数为0,则有
$$w^TX^TX=Y^TX$$
从而
$$(w^TX^TX)^T=(Y^TX)^T$$
进而可以求得
$$W=(X^TX)^{-1}X^TY$$
上面的数学过程用代码表示如下：

x = [1,2,3,4,5,6,7,8,9,10]
y = [10,11.5,12,13,14.5,15.5,16.8,17.3,18,18.7]
X = np.vstack([np.ones(len(x)),x]).T
Y = np.array(y).T
W=np.dot(np.matrix(np.dot(X.T,X))**-1,np.dot(X.T,Y))
yi=np.dot(X,W.T)#这里公式里是不需要转置的，但由于矩阵运算时W自动保存成一行多列的矩阵，所以多转置一下，配合原公式的计算。
print(X)
print(Y)
print(W)
print(yi)#拟合出的预测点
plt.plot(x,y,'o',label='data',markersize=10)
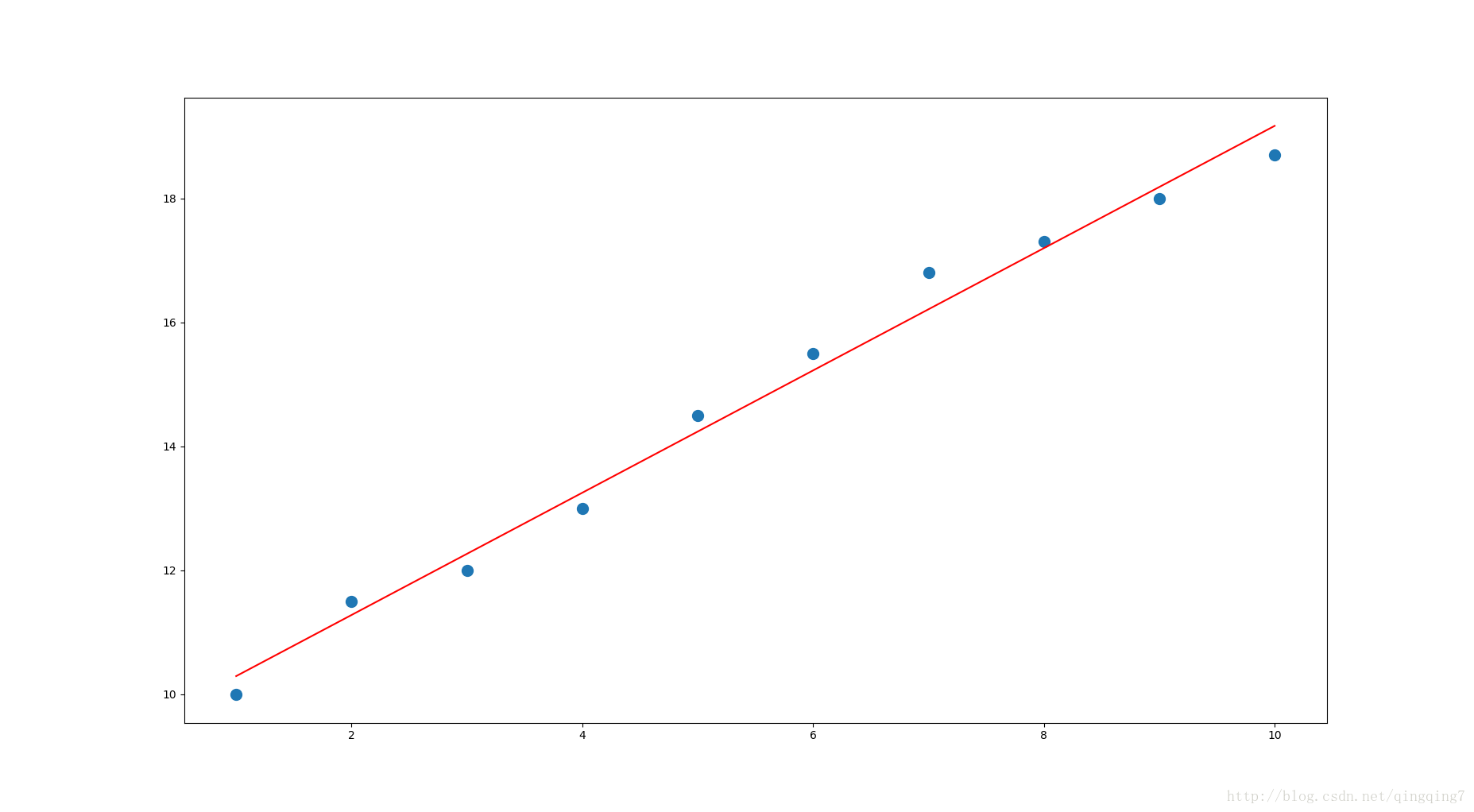
plt.plot(x,yi,'r',label='line')
plt.show()

结果如下：

X=
[[  1.   1.]
 [  1.   2.]
 [  1.   3.]
 [  1.   4.]
 [  1.   5.]
 [  1.   6.]
 [  1.   7.]
 [  1.   8.]
 [  1.   9.]
 [  1.  10.]]
Y=
[ 10.   11.5  12.   13.   14.5  15.5  16.8  17.3  18.   18.7]
W=
[[ 9.30666667  0.98606061]]
yi=
[[ 10.29272727]
 [ 11.27878788]
 [ 12.26484848]
 [ 13.25090909]
 [ 14.2369697 ]
 [ 15.2230303 ]
 [ 16.20909091]
 [ 17.19515152]
 [ 18.18121212]
 [ 19.16727273]]

3、多元线性回归

将一元线性回归及回归系数的计算公式推广到多元线性回归也是一样。
损失函数可表示如下：

$$L=\sum_{i=1}^m (y_i-W^T x_i)^2\\ $$
对L求导有
$$\begin{matrix} \frac{\partial L}{\partial W} &=&2\sum_{i=1}^m(y_i-W^Tx_i)(-1)\frac{\partial (W^Tx_i)}{\partial W}\\ &=&2\sum_{i=1}^m(W^Tx_i-y_i)\frac{\partial (W^Tx_i)}{\partial W}\\ \end{matrix}$$
不防令 $W^Tx_i-y_i=e_i$,则上式可化简为
$$\begin{matrix} \frac{\partial L}{\partial W} &=&2\sum_{i=1}^m e_i \frac{\partial (W^Tx_i)}{\partial W}\\ &=&2\sum_{i=1}^m e_i \frac{\partial (w_0+w_1x_{i1}+\cdots+w_p x_{ip})}{\partial W}\\ \end{matrix}$$
先计算 $\frac{\partial L}{\partial W}$各分量
$$\begin{matrix} \frac{\partial L}{\partial w_0}&=&2\sum_{i=1}^m e_i \frac{\partial (w_0+w_1x_{i1}+\cdots+w_p x_{ip})}{\partial w_0}&=&2\sum_{i=1}^m e_i *1\\ \frac{\partial L}{\partial w_1}&=&2\sum_{i=1}^m e_i \frac{\partial (w_0+w_1x_{i1}+\cdots+w_p x_{ip})}{\partial w_1}&=&2\sum_{i=1}^m e_i *x_{i1}\\ \cdots&=&\cdots&=&\cdots\\ \frac{\partial L}{\partial w_p}&=&2\sum_{i=1}^m e_i \frac{\partial (w_0+w_1x_{i1}+\cdots+w_p x_{ip})}{\partial w_p}&=&2\sum_{i=1}^m e_i *x_{ip}\\ \end{matrix}$$
故 $\frac{\partial L}{\partial W}$可写成
$$\begin{matrix} \frac{1}{2}\frac{\partial L}{\partial W} &=& \left[ \begin{matrix} \sum_{i=1}^m e_i *1\\ \sum_{i=1}^m e_i *x_{i1}\\ \cdots\\ \sum_{i=1}^m e_i *x_{ip}\\ \end{matrix}\right]\\ &=& \left[ \begin{matrix} e_1+e_x+\cdots+e_m\\ e_1x_{11}+e_2x_{21}+\cdots+e_mx_{m1}\\ \cdots\\ e_1x_{1p}+e_2x_{2p}+\cdots+e_mx_{mp}\\ \end{matrix}\right]\\ &=& \left[ \begin{matrix} 1+x_{11}+x_{12}+\cdots+x_{1p}\\ 1+x_{21}+x_{22}+\cdots+x_{2p}\\ \cdots\\ 1+x_{m1}+x_{m2}+\cdots+x_{mp}\\ \end{matrix}\right]^T* \left[ \begin{matrix} e_1\\ \cdots\\ e_m\\ \end{matrix}\right]\\ \end{matrix}$$
记
$$\left[ \begin{matrix} 1,x_{11},x_{12},\cdots,x_{1p}\\ 1,x_{21},x_{22},\cdots,x_{2p}\\ \cdots\\ 1,x_{m1},x_{m2},\cdots,x_{mp}\\ \end{matrix}\right] =X$$
$$\left[ \begin{matrix} e_1\\ \cdots\\ e_m\\ \end{matrix}\right]=E$$
则
$$\frac{1}{2}\frac{\partial L}{\partial W}=X^TE$$

3.1、当矩阵满秩时（数据点的个数大于x的维度时）

令导数为0的方程组有足够的已知条件求解，令导数为0，则有

$$X^TE=0$$
而
$$\begin{matrix} E&=&\left[ \begin{matrix} e_1\\ \cdots\\ e_m\\ \end{matrix}\right]\\ &=& \left[ \begin{matrix} w_0+w_1x_{11}+\cdots +w_px_{1p}-y_1\\ \cdots\\ w_0+w_1x_{m1}+\cdots +w_px_{mp}-y_m\\ \end{matrix}\right]\\ &=& \left[ \begin{matrix} w_0+w_1x_{11}+\cdots +w_px_{1p}\\ \cdots\\ w_0+w_1x_{m1}+\cdots +w_px_{mp}\\ \end{matrix}\right]- \left[ \begin{matrix} y_1\\ \cdots\\ y_m\\ \end{matrix}\right]\\ &=&XW-Y \end{matrix}$$
则有
$$X^T(XW-Y)=0\\ X^TXW-X^TY=0\\ X^TXW=X^TY\\ $$
从而有
$$W=(X^TX)^{-1}X^TY$$

3.2、当矩阵不满秩时

此时利用导数为0方程组个数不够，不能够全部解出参数，
可利用梯度下降法求近似最优解

$$W=W-\alpha \frac{\partial L}{\partial W}=W-2\alpha X^TE$$
而梯度下降步长初始化可随机设置，因而上式不防写成
$$W=W-\alpha \frac{\partial L}{\partial W}=W-\alpha X^TE$$

线性回归的并行化

pyspark.ml中的线性回归

#-*-coding:utf-8-*-

from pyspark import SparkContext
from pyspark.sql import SparkSession
from pyspark.ml.linalg import Vectors
from pyspark.ml.regression import LinearRegression

if __name__=="__main__":
    sc=SparkContext(appName="myApp")
    spark=SparkSession.builder.enableHiveSupport().getOrCreate()
    df = spark.createDataFrame([(1.0, 2.0, Vectors.dense(1.0)),(0.0, 2.0, Vectors.sparse(1, [], []))], ["label", "weight", "features"])
    lr = LinearRegression(maxIter=5, regParam=0.0, solver="normal", weightCol="weight")
    model = lr.fit(df)
    print(model.coefficients)
    print(model.intercept)
    test0 = spark.createDataFrame([(Vectors.dense(-1.0),)], ["features"])
    print(model.transform(test0).head().prediction)

spark中使用回归方法案例

参考《算法模型—回归模型—spark回归案例》

局部加权回归（LWR）

来源：https://www.cnblogs.com/sumai/p/5211558.html

RANSAC拟合高鲁棒性回归

来源：
这是对回归分析的提升，使得模型具有更好的抗干扰能力。
RANSAC(Random Sample Consenus)，它是根据一组包含异常数据的样本数据集，计算出数据的数学模型参数，得到有效样本数据的算法。使用数据的一个子集(内点,Ran)来进行回归模型的拟合。

RANSAC算法的工作流程如下：
1、从数据集中随机抽取样本构建内点集合拟合模型。
2、使用剩余的数据对上一步得到的模型进行测试，并将落在预定公差范围内的样本点增加到内点集合中。
3、使用全部的内点集合数据再次进行模型的拟合。
4、使用内点集合来估计模型的误差。
5、如果模型性能达到了用户设定的特定阈值或者迭代的次数达到了预定的次数，则算法终止，否则重复从第一步开始。

from sklearn.linear_model import RANSACRegressor
'''
max_trials设置最大迭代次数为100
min_samples随机抽取内点的最小样本数为50
residual_metric计算拟合曲线与样本点的距离的绝对值
residual_threshold设置预定公差，小于这个值才被加入到内点集合
'''
ransac = RANSACRegressor(LinearRegression(),max_trials=100,min_samples=50,
                        residual_metric=lambda x:np.sum(np.abs(x),axis=1),
                        residual_threshold=5.0,random_state=0)
ransac.fit(X,Y)
inlier_mask = ransac.inlier_mask_
outlier_mask = np.logical_not(inlier_mask)
line_X = np.arange(3,10,1)
line_y_ransac = ransac.predict(line_X[:,np.newaxis])
plt.scatter(X[inlier_mask],Y[inlier_mask],c="blue",marker="o",label="内点")
plt.scatter(X[outlier_mask],Y[outlier_mask],c="lightgreen",marker="s",label="异常值")
plt.plot(line_X,line_y_ransac,color="red")
plt.xlabel("房间数")
plt.ylabel("房价")
plt.legend(loc="upper left")
plt.show()

线性回归模型性能的评估

1、残差图
通过绘制残差图能够直观的发现真实值与预测值之间的差异或垂直距离，通过真实值与预测值之间的差异来对回归模型进行评估。残差图可以作为图形分析方法，可以对回归模型进行评估、获取模型的异常值，同时还可以检查模型是否是线性的，以及误差是否随机分布。

最好的模型预测结果的残差为0，在实际应用中，这种情况是不可能发生的。但是，对于一个好的模型，我们期望误差是随机分布的，同时残差也是在y=0水平线附近波动。通过残差图也可以发现异常值，偏离y=0比较远的点。
2、均方误差(MSE)
均方误差(Mean Squared Error，MSE)：真实值与预测值差的平方和的平均值，计算公式如下

$$MSE=\frac{1}{n}\sum_{i=1}^{n}(y_i-\hat{y}_i)^2$$

from sklearn.metrics import mean_squared_error
print("train MSE:%.3f"%mean_squared_error(train_y,train_y_pred))
#train MSE:46.037
print("test MSE:%.3f"%mean_squared_error(test_y,test_y_pred))
#test MSE:35.919

除了均方误差之外，还可以通过绝对值误差来衡量模型的性能。
3、决定系数R^2
在某些情况下决定系数(coefficient of determination)$R^2$非常重要，可以将其看成一个MSE标准化版本，$R^2$是模型捕获响应方差的分数。对于训练集来说，$R^2$的取值范围为[0,1]，对于测试集来说，$R^2$取值可能为负。如果R^2越接近与1表明其模型的性能越好。$R^2$计算公式如下：

$$R^2=1-\frac{\frac{1}{n}\sum_{i=1}^{n}(y_i-\hat{y}_i)^2}{\frac{1}{n}\sum_{i=1}^{n}(y_i-\mu_i)^2}=1-\frac{MSE}{var(y)}$$

from sklearn.metrics import r2_score
print("train r2:%.3f"%r2_score(train_y,train_y_pred))
#train r2:0.473
print("test r2:%.3f"%r2_score(test_y,test_y_pred))
#test r2:0.485

线性回归优缺点

优点

• 可以快速建模，特别适用于所要建模的关系不是特别复杂并且数据量不大。
• 线性回归简单且易于理解，有利于商业决策。

缺点

• 对于非线性数据进行多项式回归设计可能比较困难，因为必须具有特征变量之间关系和数据结构的一些信息。
• 由于上述原因，当涉及到数据复杂度较高时，这些模型的性能不如其他模型。

Generalized Linear Models ( 广义线性模型 )

来源：apache官网中文翻译
介绍sklearn中的广义线性模型。
在整个模块中，我们指定coef_代表向量$w=(w_1,\dots,w_p)$, intercept_代表$w_0$ 。

Ordinary Least Squares ( 普通最小二乘法 )

LinearRegression类的成员函数 fit 以数组X和y为输入，并将线性模型的系数 w 存储在其成员变量coef_中：

>>> from sklearn import linear_model
>>> reg = linear_model.LinearRegression()
>>> reg.fit ([[0, 0], [1, 1], [2, 2]], [0, 1, 2])
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
>>> reg.coef_
array([ 0.5,  0.5])

然而，最小二乘的系数估计依赖于模型特征项的独立性。当特征项相关并且设计矩阵X 的列近似的线性相关时，设计矩阵便接近于一个奇异矩阵，因此最小二乘估计对观测点中的随机误差变得高度敏感，产生大的方差。例如，当没有试验设计的收集数据时，可能会出现这种多重共线性(multicollinearity )的情况。
Ordinary Least Squares Complexity ( 普通最小二乘法复杂度 )
该方法通过对X进行 singular value decomposition ( 奇异值分解 ) 来计算最小二乘法的解。如果 X 是大小为(n, p) 的矩阵，则该方法的复杂度为o(np^2) ，假设$n\geq p$。

Ridge Regression ( 岭回归 )

岭回归通过对系数的大小施加惩罚来解决普通最小二乘的一些问题。 ridge coefficients ( 岭系数 ) 最小化一个带罚项(就是我们所说的正则项)的残差平方和，

$$min_w ||w^TX-y||_2^2+\alpha ||w||_2^2$$
这里, $\alpha\geq 0$是控制回归系数的复杂度参数： 值越大，回归系数越均匀，越存在过拟合的可能；值越大，回归系数越简单，就量更多的系数接近0，泛化能力更强，因此系数变得对共线性变得更加鲁棒，但拟合可能没那么好。

与其他线性模型一样，Ridge 类成员函数 fit 以数组X和y为输入，并将线性模型的系数 w 存储在其成员变量coef_ 中：

>>> from sklearn import linear_model
>>> reg = linear_model.Ridge (alpha = .5)
>>> reg.fit ([[0, 0], [0, 0], [1, 1]], [0, .1, 1])
Ridge(alpha=0.5, copy_X=True, fit_intercept=True, max_iter=None,
      normalize=False, random_state=None, solver='auto', tol=0.001)
>>> reg.coef_
array([ 0.34545455,  0.34545455])
>>> reg.intercept_
0.13636...

Ridge Complexity ( 岭复杂性 )
这种方法与 Ordinary Least Squares ( 普通最小二乘方法 ) 的复杂度相同。
Setting the regularization parameter: generalized Cross-Validation ( 设置正则化参数：广义交叉验证 )

>>> from sklearn import linear_model
>>> reg = linear_model.RidgeCV(alphas=[0.1, 1.0, 10.0])
>>> reg.fit([[0, 0], [0, 0], [1, 1]], [0, .1, 1])      
RidgeCV(alphas=[0.1, 1.0, 10.0], cv=None, fit_intercept=True, scoring=None,
    normalize=False)
>>> reg.alpha_                                     
0.1

Lasso

Lasso 是估计稀疏系数的线性模型。它在一些情况下是有用的，因为它倾向于使用具有较少回归系数的解决方案，有效地减少给定解决方案所依赖的变量的数量。为此，Lasso 及其变体是 compressed sensing ( 压缩感测领域 ) 的基础。在某些条件下，它可以恢复精确的非零权重集（参见 Compressive sensing: tomography reconstruction with L1 prior (Lasso) ( 压缩感测：使用 L1 先验（ Lasso ）进行断层扫描重建 ) ）。

在数学上，它由一个使用$L_1$先验作为正则化项的线性模型组成。最小化的目标函数是：

$$min_s \frac{1}{2n_{sample}}||w^Tx-y||_2^2 +\alpha ||w||_1$$
因此，lasso estimate 解决了加上罚项 $\alpha ||w||_1$的最小二乘法的最小化，其中， $\alpha$是常数， $||w||_1$是回归系数的 $L_1$范数,即回归系数各元素的绝对值之和。
Lasso 类中的实现使用坐标下降作为算法来拟合系数。查看 Least Angle Regression ( 最小角度回归 ) 用于另一个实现：

>>> from sklearn import linear_model
>>> reg = linear_model.Lasso(alpha = 0.1)
>>> reg.fit([[0, 0], [1, 1]], [0, 1])
Lasso(alpha=0.1, copy_X=True, fit_intercept=True, max_iter=1000,
   normalize=False, positive=False, precompute=False, random_state=None,
   selection='cyclic', tol=0.0001, warm_start=False)
>>> reg.predict([[1, 1]])
array([ 0.8])

对于较低级别的任务也很有用的是函数 lasso_path 来计算可能值的完整路径上的系数。

注意

• Feature selection with Lasso ( 功能套索和弹性网 )
  由于 Lasso 回归生成稀疏模型，因此可以用于实现特征选择，如 L1-based feature selection ( 基于 L1 的特征选择 ) 中所详述的。

注意

• Randomized sparsity ( 随机稀释 )
  对于特征选择或稀疏恢复，使用 Randomized sparse models ( 随机稀疏模型 ) 可能很有趣。

Setting regularization parameter ( 设置正则化参数 )
alpha 参数控制 degree of sparsity of the coefficients estimated ( 估计的系数的稀疏度 ) 。
Using cross-validation ( 使用交叉验证 )

scikit-learn 通过交叉验证来公开设置 Lasso alpha 参数的对象：LassoCV 和 LassoLarsCV 。 LassoLarsCV 是基于下面解释的 Least Angle Regression ( 最小角度回归 ) 算法。
对于具有许多共线回归的高维数据集， LassoCV 最常见。然而， LassoLarsCV 具有探索更相关的 alpha 参数值的优点，并且如果样本数量与观察次数相比非常小，则通常比 LassoCV 快。

Information-criteria based model selection ( 基于信息标准的模型选择 )
估计器 LassoLarsIC 建议使用 Akaike 信息准则（AIC）和贝叶斯信息准则（BIC）。当使用 k-fold 交叉验证时，正则化路径只计算一次而不是 k + 1 次，所以找到 α 的最优值是一个计算上更便宜的替代方法。然而，这样的标准需要对解决方案的自由度进行适当的估计，为大样本（渐近结果）导出，并假设模型是正确的，即数据实际上是由该模型生成的。当问题条件差时，它们也倾向于打破（比样本更多的特征）。

Multi-task Lasso ( 多任务套索 )

MultiTaskLasso 是一个线性模型，它联合估计多个回归问题的稀疏系数：y 是一个二维数组，shape(n_samples，n_tasks)。约束是所选的特征对于所有的回归问题都是相同的，也称为 tasks ( 任务 )。
下图比较了使用简单 Lasso 或 MultiTaskLasso 获得的 W 中非零的位置。 Lasso 估计产生分散的非零，而 MultiTaskLasso 的非零是全列。


在数学上，它由一个线性模型组成，训练有混合的 $L_1,L_2$之前的正则化。目标函数最小化是：

$$min_s \frac{1}{2n_{sample}}||w^Tx-y||_{Fro}^2 +\alpha ||w||_{21}$$
其中 Fro表示 Frobenius 规范：
$$||A||_{Fro}=\sqrt{\sum_{ij}a_{ij}^2}$$
而 $L_1,L_2$混合形式如下：
$$||A||_{21}=\sum_i \sqrt{\sum_{j}a_{ij}^2}$$
MultiTaskLasso 类中的实现使用坐标下降作为拟合系数的算法。

Elastic Net ( 弹性网 )

ElasticNet 是一种线性回归模型，以 L1 和 L2 组合为正则化项。这种组合允许学习一个稀疏模型，其中很少的权重是非零的，如 Lasso ，同时仍然保持 Ridge 的正则化属性。我们使用 l1_ratio 参数控制 L1 和 L2 的凸组合。
当有多个相互关联的特征时，Elastic-net 是有用的。 Lasso 有可能随机选择其中之一，而 elastic-net 则很可能选择两者。

Lasso 和 Ridge 之间的一个实际的优势是允许 Elastic-Net 继承 Ridge 在一些旋转下的稳定性。
在这种情况下，最小化的目标函数

$$min_s \frac{1}{2n_{sample}}||w^Tx-y||_{2}^2 +\alpha \rho||w||_{1}+\frac{\alpha (1-\rho)}{2}||w||_{2}^2$$

ElasticNetCV 类可用于通过交叉验证来设置参数 alpha( $\alpha$)和 l1_ratio $(\rho )$。

Multi-task Elastic Net ( 多任务弹性网 )

MultiTaskElasticNet 是一个弹性网络模型，可以联合估计多个回归问题的稀疏系数： Y 是 2D array，shape(n_samples, n_tasks)。constraint ( 约束 ) 是所选的特征对于所有的回归问题都是相同的，也称为 tasks ( 任务 )。
目标函数最小化是：

$$min_s \frac{1}{2n_{sample}}||w^Tx-y||_{Fro}^2 +\alpha \rho||w||_{21}+\frac{\alpha (1-\rho)}{2}||w||_{Fro}^2$$

MultiTaskElasticNet 类中的实现使用坐标下降作为拟合系数的算法。
MultiTaskElasticNetCV 类可用于通过交叉验证来设置参数 alpha( $\alpha$) 和l1_ratio($\rho$)。

Least Angle Regression ( 最小角度回归 )

Least-angle regression ( 最小二乘回归 ) ( LARS ) 是由 Bradley Efron，Trevor Hastie，Iain Johnstone 和 Robert Tibshirani 开发的高维数据回归算法。
LARS 的优点是：

• 在$p >> n$的情况下（即，当维数显著大于点数时）的数值效率较高
• 它在计算上与正向选择一样快，并且具有与普通最小二乘法相同的复杂度。
• 它产生一个完整的分段线性解决路径，这在交叉验证或类似的调试模型尝试中很有用。
• 如果两个变量与响应几乎相等，那么它们的系数应该以大致相同的速率增加。因此，算法的行为就像直觉所期望的那样，并且也更稳定。
• 它很容易被修改为其他估计器产生解决方案，如 Lasso 。

LARS 方法的缺点包括：

• 因为 LARS 是基于对残差进行迭代重新设计的，所以它似乎对噪声的影响特别敏感。 Weisberg 在 Efron 等人的讨论部分详细讨论了这个问题。 (2004) Annals of Statistics article 。

LARS 模型可以使用估计器 Lars 或其低级实现 lars_path 来使用。

LARS Lasso

LassoLars 是使用 LARS 算法实现的 lasso model ( 套索模型 ) ，与基于 coordinate_descent 的实现不同，这产生了精确的解，其作为其系数范数的函数是分段线性的。

>>> from sklearn import linear_model
>>> reg = linear_model.LassoLars(alpha=.1)
>>> reg.fit([[0, 0], [1, 1]], [0, 1]) 
LassoLars(alpha=0.1, copy_X=True, eps=..., fit_intercept=True,
     fit_path=True, max_iter=500, normalize=True, positive=False,
     precompute='auto', verbose=False)
>>> reg.coef_   
array([ 0.717157...,  0.        ])

Lars 算法提供了沿着正则化参数的系数的完整路径，几乎是免费的，因此一个常见的操作包括使用函数 lars_path 检索路径。
Mathematical formulation ( 数学表达 )

该算法类似于 forward stepwise regression ( 前向逐步回归 ) ，而不是在每个步骤中包含变量，估计参数在等于每个与残差相关的方向上增加。
代替给出向量结果，LARS 解决方案由表示参数向量的 L1 norm ( 范数 ) 的每个值的解的曲线组成。完整系数路径存储在具有 size(n_features, max_features + 1) 的数组 coef_path_ 中。第一列始终为零。

Orthogonal Matching Pursuit (OMP) ( 正交匹配追踪（OMP） )

OrthogonalMatchingPursuit ( 正交匹配追踪 ) 和 orthogonal_mp 实现了 OMP 算法，用于近似线性模型的拟合，并对非零系数（即 L 0 伪范数）施加约束。
作为 Least Angle Regression ( 最小角度回归 ) 的前向特征选择方法，正交匹配追踪可以用固定数量的非零元素逼近最优解矢量：

$$arg~min ||y-X\gamma||_2^2~subject ~to ~||\gamma||_0\leq n_{nonezero_coefs}$$
或者，正交匹配追踪可以针对特定错误而不是特定数量的非零系数。这可以表示为：
$$arg~min ||\gamma||_0~subject ~to ~||y-X\gamma||_2^2\leq tol$$
OMP 基于一个贪心算法，每个步骤都包含与当前残差最相关的原子。它类似于更简单的匹配追求（ MP ）方法，但是在每次迭代中更好，使用在先前选择的词典元素的空间上的正交投影重新计算残差。
OMP 基于一个贪心算法，每个步骤都包含与当前残差最相关的原子。它类似于更简单的匹配追求（ MP ）方法，但是在每次迭代中更好，使用在先前选择的词典元素的空间上的正交投影重新计算残差。

Bayesian Regression ( 贝叶斯回归 )

贝叶斯回归技术可以用于在估计过程中包括正则化参数：正则化参数不是硬的设置，而是调整到手头的数据。
这可以通过对模型的超参数引入 uninformative priors ( 不知情的先验 ) 来完成。Ridge Regression 中使用的$L_2$正则化等价于在精度为 的参数 w 之前，在高斯下找到最大 a-postiori 解。而不是手动设置 lambda ，可以将其视为从数据估计的随机变量。
为了获得一个完全概率模型，输出y被假定为高斯分布在 $X w$ 周围：

$$p(y|X,w,\alpha)=N(y|Xw,\alpha)$$
Alpha 再次被视为从数据估计的随机变量。
贝叶斯回归的优点是：

• 它适应了 data at hand ( 手头的数据 ) 。
• 它可以用于在估计过程中包括正则化参数。

贝叶斯回归的缺点包括：

• 模型的推论可能是耗时的。

Bayesian Ridge Regression ( 贝叶斯岭回归 )

BayesianRidge estimates ( 贝叶斯岭方差估计 ) 如上所述的回归问题的概率模型。参数 w 的先验由球面高斯给出：

$$p(w|\lambda)=N(w|0,\lambda^{-1}I)$$
选择 $\alpha$和 $\lambda$的先验是 gamma distributions ( 伽马分布 ) ，即 conjugate prior for the precision of the Gaussian ( 高斯精度之前的共轭 ) 。
所得到的模型称为 Bayesian Ridge Regression ( 贝叶斯岭回归 ) ，与 classical Ridge ( 古典岭 ) 相似。参数 $w$，$\alpha$和 $\lambda$在模型拟合期间联合估计。剩余的超参数是 $\alpha$和 $\lambda$之后的伽玛先验的参数。这些通常被选为 non-informative ( 非资料性 ) 的。通过最大化边际对数似然估计参数。
默认情况下，

贝叶斯回归用于回归：

>>> from sklearn import linear_model
>>> X = [[0., 0.], [1., 1.], [2., 2.], [3., 3.]]
>>> Y = [0., 1., 2., 3.]
>>> reg = linear_model.BayesianRidge()
>>> reg.fit(X, Y)
BayesianRidge(alpha_1=1e-06, alpha_2=1e-06, compute_score=False, copy_X=True,
       fit_intercept=True, lambda_1=1e-06, lambda_2=1e-06, n_iter=300,
       normalize=False, tol=0.001, verbose=False)

安装后，该模型可用于预测新值：

>>> reg.predict ([[1, 0.]])
array([ 0.50000013])

模型的权重 w 可以访问：

>>> reg.coef_
array([ 0.49999993,  0.49999993])

由于贝叶斯框架发现的权重与普通最小二乘法发现的权重略有不同。然而，贝叶斯岭回归对于不适当的问题更为强大。

Automatic Relevance Determination - ARD ( 自动相关性测定 - ARD )

ARDRegression 与 Bayesian Ridge Regression ( 贝叶斯岭回归 ) 非常相似，但可以导致更稀疏的权重 w 。 ARDREgression 通过放弃高斯为球面的假设，构成了与 w 之前不同的先验。
相反，假定 w 上的分布是轴平行的椭圆高斯分布。
这意味着每个权重$w_i$从高斯分布绘制，以零为中心，精度为$\lambda_i$ ：

$$p(w|\lambda)=N(w|0,A^{-1})$$
与 $diag(A)=\lambda=\{\lambda_1,\dots,\lambda_p\}$。
与贝叶斯岭回归相反，每个 $w_i$的坐标都有自己的标准偏差 $\lambda_i$。 先前的所有 $\lambda_i$被选择为由超参数 $\lambda_1$和 $\lambda_2$给出的相同的伽马分布。

ARD 在文献中也被称为稀疏贝叶斯学习与 Relevance Vector Machine

Logistic regression ( 逻辑回归 )

Logistic regression ( 逻辑回归 ) ，尽管它的名字是回归，是一个用于分类的线性模型而不是用于回归。

Stochastic Gradient Descent - SGD ( 随机梯度下降 )

Stochastic gradient descent ( 随机梯度下降 ) 是一种简单但非常有效的拟合线性模型的方法。当 samples ( 样本 ) 数量（和 features ( 特征 ) 数量）非常大时，这是特别有用的。 partial_fit 方法 only/out-of-core 学习。
SGDClassifier 和 SGDRegressor 类提供了使用不同（凸）损失函数和不同惩罚的分类和回归的线性模型的功能。例如，当 loss=“log” 时，SGDC 分类器适合逻辑回归模型，而 loss=”hinge” 则适合线性支持向量机（ SVM ）。

Perceptron ( 感知 )

Perceptron ( 感知器 ) 是适用于大规模学习的另一种简单算法。默认：

• 它不需要 learning rate ( 学习率 ) 。
• 它不是 regularized (penalized) ( 正规化（惩罚） ) 。
• 它 updates its model only on mistakes ( 仅在错误时更新其模型 ) 。

最后一个特征意味着 Perceptron ( 感知器 ) 比 hinge loss 比 SGD 稍快一点，并且所得到的模型更加 sparser ( 稀疏 ) 。

Passive Aggressive Algorithms ( 被动侵略性算法 )

passive-aggressive algorithms ( 被动侵略算法 ) 是用于 large-scale learning ( 大规模学习 ) 的一系列算法。它们与 Perceptron ( 感知器 ) 类似，因为它们不需要 learning rate ( 学习率 ) 。然而，与 Perceptron ( 感知器 ) 相反，它们包括正则化参数 C 。
对于分类，PassiveAggressiveClassifier 可以与 loss =’hinge’ （ PA-I ）或 loss =“squared_hinge” （ PA-II ）一起使用。对于回归，PassiveAggressiveRegressor 可以与 loss =’epsilon_insensitive’ （ PA-I ）或 loss =’squared_epsilon_insensitive’ （ PA-II ）一起使用。

Robustness regression: outliers and modeling errors ( 鲁棒性回归：异常值和建模误差 )

Robust regression ( 鲁棒性回归 ) 有兴趣在存在 presence of corrupt data ( 腐败数据 ) 的情况下拟合回归模型：outliers ( 异常值 ) 或模型中的错误。

Different scenario and useful concepts ( 不同的场景和有用的概念 )

处理由异常值损坏的数据时，请记住不同的事项：
Outliers in X or in y?

Outliers in the y direction

Outliers in the X direction

Fraction of outliers versus amplitude of error ( 异常值与误差幅度的分数 )
The number of outlying points matters, but also how much they are outliers. ( 离岸点的数量很重要，但也是离群点多少 )

Small outliers

Large outliers
robust fitting 的一个重要概念就是 breakdown point ( 分解点 ) ：可以离开的数据的分数，以适合开始丢失内部数据。

注意，一般来说，在高维度设置（大 n_features ）中的 robust fitting ( 鲁棒拟合 ) 是非常困难的。这里的 robust models ( 健壮模型 ) 可能无法在这些设置中使用。

RANSAC: RANdom SAmple Consensus

RANSAC ( RANdom SAmple Consensus ) 适合来自完整数据集的来自随机子集的模型。
RANSAC 是一种 non-deterministic ( 非确定性 ) 算法，只产生具有一定概率的合理结果，这取决于迭代次数（参见 max_trials 参数）。它通常用于线性和非线性回归问题，在摄影测量计算机视觉领域尤其受欢迎。
该算法将完整的输入采样数据分解为可能受到噪声的一组内联集，以及异常值。由数据的错误测量或无效假设引起。然后，所得到的模型仅来自确定的内部估计。

Details of the algorithm ( 算法的细节 )
每次迭代执行以下步骤：

• 从原始数据中选择 min_samples random samples ( 随机样本 ) ，并检查数据集是否有效（请参阅 is_data_valid）。
• 将模型拟合为 random subset ( 随机子集 ) （ base_estimator.fit ），并检查估计模型是否有效（请参阅 is_model_valid ）。
• 通过计算 estimated model ( 估计模型 ) 的残差（base_estimator.predict（X） - y））将所有数据作为内部值或异常值进行分类 - all 绝对残差小于 residual_threshold ( 残差阈值 ) 的数据样本均被视为内部值。
• 如果 Inlier 样本数量最大，则将拟合模型保存为最佳模型。如果当前估计的模型具有相同数量的内部值，则只有当其具有较好的分数时才被认为是最佳模型。

这些步骤最大次数（ max_trials ）执行，或直到满足特殊停止条件之一（参见 stop_n_inliers 和 stop_score ）。最终模型使用先前确定的最佳模型的所有 Inlier 样本（一致集合）进行估计。

is_data_valid 和 is_model_valid 函数允许识别和拒绝随机子样本的退化组合。如果估计的模型不需要用于识别退化情况，则应使用 is_data_valid ，因为它在拟合模型之前被调用，从而导致更好的计算性能。

Theil-Sen estimator: generalized-median-based estimator ( Theil-Sen 估计：广义中位数估计 )

TheilSenRegressor 估计器使用 generalization of the median in multiple dimensions ( 多维度中值的泛化 ) 。因此，多变量离群值是非常 robust ( 鲁棒 ) 的。但是请注意，估计器的鲁棒性随着问题的维数而迅速降低。它失去了其鲁棒性，并且在高维度上变得不如普通的最小二乘法。
Theoretical considerations ( 理论考虑 )
TheilSenRegressor 在渐近效率方面与普通最小二乘法（ OLS ）相当，作为无偏估计。与 OLS 相反，Theil-Sen 是一种非参数方法，这意味着它不会对数据的基本分布做出假设。由于 Theil-Sen 是一个基于中位数的估计器，它对于破坏的数据而言更为强大。在单变量设置中，Theil-Sen 在简单线性回归的情况下的崩溃点约为 29.3% ，这意味着它可以容忍高达 29.3% 的任意损坏的数据。

在 scikit-learn 中 TheilSenRegressor 的实现遵循多变量线性回归模型 的推广，使用空间中值，这是中位数到多维度的推广]。
在时间和空间复杂性方面， Theil-Sen scales 根据:

$$\left( \begin{matrix} n_{samples}\\n_{subsamples} \end{matrix} \right)$$
这使得对于大量样品和特征的问题进行彻底的应用是不可行的。因此，可以通过仅考虑所有可能组合的随机子集来选择子群体的大小来限制时间和空间复杂性。

Huber Regression ( 胡伯回归 )

HuberRegressor 与 Ridge 不同，因为它将线性损失应用于被分类为异常值的样本。如果该样本的绝对误差小于某一阈值，则样本被归类为一个异常值。它不同于 TheilSenRegressor 和 RANSACRegressor ，因为它不会忽视异常值的影响，但对它们的重视程度较小。

Polynomial regression: extending linear models with basis functions ( 多项式回归：用基函数扩展线性模型 )

机器学习中的一种常见模式是使用训练数据非线性函数的线性模型。这种方法保持线性方法的 generally fast performance ( 一般快速性能 ) ，同时允许它们适应更广泛的数据。
例如，可以通过从 constructing polynomial features ( 系数构造多项式特征 ) 来扩展简单的线性回归。在标准线性回归的情况下，您可能有一个类似于二维数据的模型：

$$\hat{y}(w,x)=w_0+w_1x_1+w_2x_2$$
如果我们想要将数学拟合为抛物面而不是平面，我们可以将 second-order polynomials ( 二阶多项式 ) 的特征组合起来，使得模型如下所示：
$$\hat{y}(w,x)=w_0+w_1x_1+w_2x_2+w_3x_1x_2+w_4x_1^2+w_5x_2^2$$
（有时令人惊讶）的观察是，这仍然是一个线性模型：要看到这一点，想象一下创建一个新的变量
$$z=[x_1,x_2,x_1x_2,x_1^2,x_2^2]$$
通过对数据的重新标注，可以写出我们的问题
$$\hat{y}(w,x)=w_0+w_1z_1+w_2z_2+w_3z_3+w_4z_4+w_5z_5$$
我们看到所得到的多项式回归与上面我们考虑过的线性模型相同（即模型在 w 中是线性的），并且可以通过相同的技术来解决。通过考虑使用这些基本功能构建的更高维度空间内的线性拟合，该模型具有适应更广泛范围的数据的灵活性。

以下是使用不同程度的多项式特征将这一想法应用于一维数据的示例：

该图是使用 PolynomialFeatures 预处理器创建的。该预处理器将输入数据矩阵转换为给定度的新数据矩阵。它可以使用如下：

>>> from sklearn.preprocessing import PolynomialFeatures
>>> import numpy as np
>>> X = np.arange(6).reshape(3, 2)
>>> X
array([[0, 1],
       [2, 3],
       [4, 5]])
>>> poly = PolynomialFeatures(degree=2)
>>> poly.fit_transform(X)
array([[  1.,   0.,   1.,   0.,   0.,   1.],
       [  1.,   2.,   3.,   4.,   6.,   9.],
       [  1.,   4.,   5.,  16.,  20.,  25.]])

X 的特征已经从$[x_1,x_2]$转换为$[1,x_1,x_2,x_1^2,x_1x_2,x_2^2]$，现在可以在任何线性模型中使用。
这种预处理可以使用 Pipeline 进行简化。可以创建表示简单多项式回归的单个对象，并使用如下：

>>> from sklearn.preprocessing import PolynomialFeatures
>>> from sklearn.linear_model import LinearRegression
>>> from sklearn.pipeline import Pipeline
>>> import numpy as np
>>> model = Pipeline([('poly', PolynomialFeatures(degree=3)),
...                   ('linear', LinearRegression(fit_intercept=False))])
>>> # fit to an order-3 polynomial data
>>> x = np.arange(5)
>>> y = 3 - 2 * x + x ** 2 - x ** 3
>>> model = model.fit(x[:, np.newaxis], y)
>>> model.named_steps['linear'].coef_
array([ 3., -2.,  1., -1.])

训练多项式特征的线性模型能够准确地恢复输入多项式系数。
在某些情况下，没有必要包含任何单个功能的更高的功能，而只包含所有交互功能，这些功能可以在多达 d 个不同的功能中进行叠加。这些可以通过设置 interaction_only = True 从 PolynomialFeatures 获得。
例如，当处理布尔特征时，所有 n 的$x_i^n=x_i$因此是无用的;但 $x_i x_j$ 表示两个布尔值的连接。这样，我们可以使用线性分类器来解决 XOR 问题：

>>> from sklearn.linear_model import Perceptron
>>> from sklearn.preprocessing import PolynomialFeatures
>>> import numpy as np
>>> X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
>>> y = X[:, 0] ^ X[:, 1]
>>> y
array([0, 1, 1, 0])
>>> X = PolynomialFeatures(interaction_only=True).fit_transform(X).astype(int)
>>> X
array([[1, 0, 0, 0],
       [1, 0, 1, 0],
       [1, 1, 0, 0],
       [1, 1, 1, 1]])
>>> clf = Perceptron(fit_intercept=False, n_iter=10, shuffle=False).fit(X, y)

And the classifier “predictions” are perfect: ( 分类器“预测”是完美的 ) ：

>>> clf.predict(X)
array([0, 1, 1, 0])
>>> clf.score(X, y)
1.0

最小二乘法多项式曲线拟合

多项式曲线拟合与多元线性回归拟合不同点在于，多元线性回归自变量有多个，因变量是多个自变量的线性组合，其形式为$y=w_0+w_1x_1+\dots+w_nx_n$；而多项式拟合自变量还是一个，只不过因变量可以看作是自变量不同多项式的线性组合，其形式为$y=w_0+w_1x+w_2x^2+\dots+w_kx^k$。但利用矩阵计算时，如果满秩，两者系数的表达方式是一样的，$w=\left(X^T X\right)^{-1}X^TY$

概念

默认地认为因变量是自变量的多项式的线性组全，即有如下形式$y=w_0+w_1x+w_2x^2+\dots+w_kx^k$。最小二乘法多项式曲线拟合，根据给定的m个点,并不要求这条曲线精确地经过这些点，而是拟合曲线$y= \phi(x)$上的数据点到原数据点的误差平方和最小。即有

$$\begin{matrix} min_{\phi}\sum_{i=1}^m δ_i^2&=&min_{\phi}\sum_{i=1}^m (\phi(x_i)-y_i)^2\\ &=&min_{\phi}\sum_{i=1}^m (w_0+w_1x_i+w_2x_i^2+\dots+w_k x_i^k-y_i)^2---(1) \end{matrix}$$

回归系数求解

求最值问题，如果直接求解那么必然在可能的极值点获得（此时没有边界限制）。
对（1）式求偏导，如下

$$\begin{matrix} \sum_{i=1}^m 2(w_0+w_1x_i+w_2x_i^2+\dots+w_kx_i^k-y_i)\frac{\partial (w_0+w_1x_i+w_2x_i^2+\dots+w_kx_i^k)}{\partial w} &=& 0\\ \end{matrix}$$
为便于理解，我们每次都只对w的一个维度求偏导，则有
$$\begin{matrix} \sum_{i=1}^m (w_0+w_1x_i+w_2x_i^2+\dots+w_kx_i^k-y_i)\frac{\partial (w_0+w_1x_i+w_2x_i^2+\dots+w_kx_i^k)}{\partial w_0} &=& 0\\ \sum_{i=1}^m (w_0+w_1x_i+w_2x_i^2+\dots+w_kx_i^k-y_i)\frac{\partial (w_0+w_1x_i+w_2x_i^2+\dots+w_kx_i^k)}{\partial w_1} &=& 0\\ \dots &=&0 \\ \sum_{i=1}^m (w_0+w_1x_i+w_2x_i^2+\dots+w_kx_i^k-y_i)\frac{\partial (w_0+w_1x_i+w_2x_i^2+\dots+w_kx_i^k)}{\partial w_k} &=& 0\\ \end{matrix}$$
即
$$\begin{matrix} \sum_{i=1}^m (w_0+w_1x_i+w_2x_i^2+\dots+w_kx_i^k-y_i)*1 &=& 0\\ \sum_{i=1}^m (w_0+w_1x_i+w_2x_i^2+\dots+w_kx_i^k-y_i)*x_i&=& 0\\ \dots &=&0 \\ \sum_{i=1}^m (w_0+w_1x_i+w_2x_i^2+\dots+w_kx_i^k-y_i)x_i^k &=& 0\\ \end{matrix}$$
即
$$\begin{matrix} w_0\sum_{i=1}^m 1+w_1\sum_{i=1}^mx_i+w_2\sum_{i=1}^mx_i^2+\dots+w_k\sum_{i=1}^mx_i^k-\sum_{i=1}^my_i*1 &=& 0\\ w_0\sum_{i=1}^m x_i+w_1\sum_{i=1}^mx_i^2+w_2\sum_{i=1}^mx_i^3+\dots+w_k\sum_{i=1}^mx_i^{k+1}-\sum_{i=1}^my_i*x_i &=& 0\\ \dots &=&0 \\ w_0\sum_{i=1}^m x_i^k+w_1\sum_{i=1}^mx_i^{k+1}+w_2\sum_{i=1}^mx_i^{k+2}+\dots+w_k\sum_{i=1}^mx_i^{2k}-\sum_{i=1}^my_i*x_i^k &=& 0\\ \end{matrix}$$
即
$$\begin{matrix} w_0\sum_{i=1}^m 1+w_1\sum_{i=1}^mx_i+w_2\sum_{i=1}^mx_i^2+\dots+w_k\sum_{i=1}^mx_i^k &=& \sum_{i=1}^my_i*1\\ w_0\sum_{i=1}^m x_i+w_1\sum_{i=1}^mx_i^2+w_2\sum_{i=1}^mx_i^3+\dots+w_k\sum_{i=1}^mx_i^{k+1} &=& \sum_{i=1}^my_i*x_i\\ \dots &=&\dots \\ w_0\sum_{i=1}^m x_i^k+w_1\sum_{i=1}^mx_i^{k+1}+w_2\sum_{i=1}^mx_i^{k+2}+\dots+w_k\sum_{i=1}^mx_i^{2k} &=& \sum_{i=1}^my_i*x_i^k\\ \end{matrix}$$

写成矩阵形式有

$$\left [ \begin{matrix} \sum_{i=1}^m 1& \sum_{i=1}^mx_i & \sum_{i=1}^mx_i^2 & \dots & \sum_{i=1}^mx_i^k \\ \sum_{i=1}^m x_i & \sum_{i=1}^mx_i^2 & \sum_{i=1}^mx_i^3 & \dots & \sum_{i=1}^mx_i^{k+1} \\ \dots & \dots & \dots & \dots & \dots \\ \sum_{i=1}^m x_i^k & \sum_{i=1}^mx_i^{k+1} & \sum_{i=1}^mx_i^{k+2} & \dots & \sum_{i=1}^mx_i^{2k} \\ \end{matrix} \right ] \left [ \begin{matrix} w_0\\ w_1\\ \dots\\ w_k\\ \end{matrix} \right ] = \left [ \begin{matrix} \sum_{i=1}^my_i*1\\ \sum_{i=1}^my_i*x_i\\ \dots\\ \sum_{i=1}^my_i*x_i^k\\ \end{matrix} \right ]$$

将这个范德蒙得矩阵化简后可得到:

$$\left [ \begin{matrix} 1& x_1 & x_1^2 & \dots &x_1^k \\ 1& x_2 & x_2^2 & \dots &x_2^k \\ \dots & \dots & \dots & \dots & \dots \\ 1& x_m & x_m^2 & \dots &x_m^k \\ \end{matrix} \right ] \left [ \begin{matrix} w_0\\ w_1\\ \dots\\ w_k\\ \end{matrix} \right ] = \left [ \begin{matrix} y_1\\ y_2\\ \dots\\ y_m\\ \end{matrix} \right ]---(2)$$
也就是说 $X*A=Y$，那么
$$A = (X^T*X)^{-1}*X^T*Y---(3)$$
便得到了系数矩阵 A A <script type="math/tex" id="MathJax-Element-119">A</script>，同时，我们也就得到了拟合曲线。
其实我想说的是看到(2)中的矩阵等式，这个等式都不用推导的，因为函数的表达式就是这样的代入，代入样本后自然会有这样的等式。
而（3）通过矩阵运算自然就能得到。
下面是网上的一段多项式回归的python代码：

# coding=utf-8

'''
作者:Jairus Chan
程序:多项式曲线拟合算法
'''
import matplotlib.pyplot as plt
import math
import numpy
import random

fig = plt.figure()
ax = fig.add_subplot(111)

#阶数为9阶
order=9

#生成曲线上的各个点
x = numpy.arange(-1,1,0.02)
y = [((a*a-1)*(a*a-1)*(a*a-1)+0.5)*numpy.sin(a*2) for a in x]
#ax.plot(x,y,color='r',linestyle='-',marker='')
#,label="(a*a-1)*(a*a-1)*(a*a-1)+0.5"

#生成的曲线上的各个点偏移一下，并放入到xa,ya中去
i=0
xa=[]
ya=[]
for xx in x:
    yy=y[i]
    d=float(random.randint(60,140))/100
    #ax.plot([xx*d],[yy*d],color='m',linestyle='',marker='.')
    i+=1
    xa.append(xx*d)
    ya.append(yy*d)

'''for i in range(0,5):
    xx=float(random.randint(-100,100))/100
    yy=float(random.randint(-60,60))/100
    xa.append(xx)
    ya.append(yy)'''

ax.plot(xa,ya,color='m',linestyle='',marker='.')


#进行曲线拟合
matA=[]
for i in range(0,order+1):
    matA1=[]
    for j in range(0,order+1):
        tx=0.0
        for k in range(0,len(xa)):
            dx=1.0
            for l in range(0,j+i):
                dx=dx*xa[k]
            tx+=dx
        matA1.append(tx)
    matA.append(matA1)

#print(len(xa))
#print(matA[0][0])
matA=numpy.array(matA)

matB=[]
for i in range(0,order+1):
    ty=0.0
    for k in range(0,len(xa)):
        dy=1.0
        for l in range(0,i):
            dy=dy*xa[k]
        ty+=ya[k]*dy
    matB.append(ty)

matB=numpy.array(matB)

matAA=numpy.linalg.solve(matA,matB)

#画出拟合后的曲线
#print(matAA)
xxa= numpy.arange(-1,1.06,0.01)
yya=[]
for i in range(0,len(xxa)):
    yy=0.0
    for j in range(0,order+1):
        dy=1.0
        for k in range(0,j):
            dy*=xxa[i]
        dy*=matAA[j]
        yy+=dy
    yya.append(yy)
ax.plot(xxa,yya,color='g',linestyle='-',marker='')

ax.legend()
plt.show()

结果如下：

随机森林回归

from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import train_test_split

#将数据集分为测试集和训练集
train_x,test_x,train_y,test_y = train_test_split(X,Y,test_size=0.3)
'''
n_estimators:估计器(树)的个数
criterion:优化目标
'''
forest = RandomForestRegressor(n_estimators=100,criterion="mse",n_jobs=1)
forest.fit(train_x,train_y)
print("train r2:%.3f"%r2_score(train_y,forest.predict(train_x)))
#train r2:0.929
print("test r2:%.3f"%r2_score(test_y,forest.predict(test_x)))
#test r2:0.227

优缺点

优点：

• 善于学习复杂且高度非线性的关系，通常可以具有很高的性能，其性能优于多项式回归，并且通常与神经网络的性能相当。

• 非常便于理解，虽然最终的训练模型可以学习较为复杂的关系，但是在训练过程中建立的决策边界很容易理解。
  缺点：

• 由于训练决策树的性质，可能很容易出现重大的过度拟合。完整的决策树模型可能过于复杂并且包含不必要的结构。有时可以通过适当的树木修剪和较大的随机森林合奏来缓解这种情况。

• 使用较大的随机森林合奏来获得更高的性能，会使速度变慢，并且需要更多的内存。

神经网络用于回归

优缺点

优点

• 由于神经网络可以有多个非线性的层（和参数），因此对非常适合对比较复杂的非线性关系建模。
• 神经网络中的数据结构基本上对学习任何类型的特征变量关系都非常灵活。
• 研究表明，为网络提供更多的训练数据（不管是增加全新的数据集还是对原始数据集进行扩张）可以提高网络性能。
• 设置也有利于提高网络性能。

缺点

• 这些模型较复杂，因此不太容易被理解。
• 网络的训练可能非常具有挑战性和计算密集性，需要对超参数进行微调并设置学习率表。
• 网络的高性能需要大量的数据来实现，在“少量数据”情况下通常不如其他机器学习算法的性能。

回归预测分析的一个例子

https://blog.csdn.net/sinat_29957455/article/details/80057728

实践记录

一般预测未来会过去的真实数据代入训练好的模型来逐步预测，而不会使用预测值，直觉的考虑是预测值没有总会有偏差。但在运用GBDT解决序列测试时，发现，用过去的预测值代替真实值代入训练的模型来预测未来，结果会更加准确。可能是因为预测值虽跟真实值有偏差，但它是一个综合结果，有点像序列平滑后结果更平均，这样综合效果的值去预测未来反而更准备。