数字信号处理7——点到向量的距离

目录

一、前言

二、点到线段的最短距离——向量法

三、点到直线的最短距离——直线法

四、点到直线最短距离——向量法

---

一、前言

       其实在工程应用中很多情况下计算点到直线或者点到线段的距离，比如在unity3d游戏软件设计中计算任意形状路径起点和终点连线距离最远的点，比如用于雷达聚类后在多目标跟踪算法中计算哪个sensor距离track最近，另外还需要知道要计算的点位于直线的哪一侧，这些计算在游戏开发或者数字信号后处理要求实时性，因此需要高效的运算。这里记录一下几种计算方法，方便需要时回忆。

需要记住的是点乘（内积）计算的一个向量在另一个向量上的投影cos，叉乘计算的是从同一点出发的两个向量,一个向量在距离另一个向量垂直距离sin。

二、点到线段的最短距离——向量法

要求：计算平面一点到两点连成的线段，哪一个端点最近；另外计算点到两点形成向量的最短距离的计算（PC）;

向量法计算在处理数据运算量多的地方相比联合求方程有显著的运算效率。

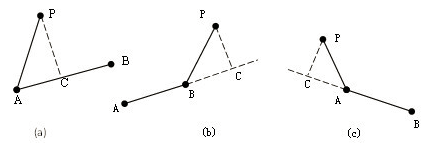
上面的 是方向上的单位向量，其意义是给所求向量确定方向。是的两个向量的内积，且   ，其中θ为向量AP与AB之间的夹角是向量长度。

根据向量的方向性可以推出以下表达，分别对应上述的(a)(b)(c)：

三、点到直线的最短距离——直线法

参考1中提供了8中不同的计算方法，可以开阔思维，但是工程中，我们更习惯使用简单的两点法求直线方程：

直线一般公式 为：

;

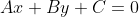直线外一点 (x0,y0) 到直线距离公式 :

;

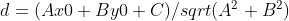假设首尾两点 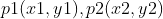, 待计算点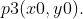

把p1,p2带入直线一般公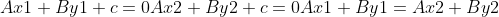式得:

， 两式得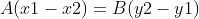

设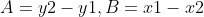 把A, B带入方程求解C: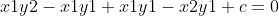

求得 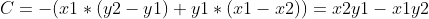, 将A,B,C带入点到直线距离公式可求得距离值：

总结起来：

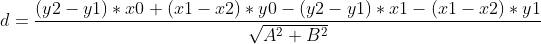
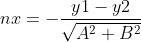
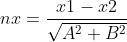
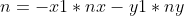
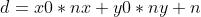
四、点到直线最短距离——向量法

向量法其实与直线法的求解结果一样，但是更直观也更容易理解。

假设首尾两点 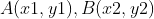, 待计算点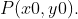

,

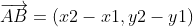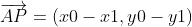
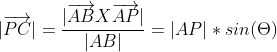
参考：

点到直线的八种计算方法（求解方法思路众多，但是运算着实麻烦）：https://zhuanlan.zhihu.com/p/26307123

点到向量距离（核心思想有，但是有一些表达错误）：https://blog.csdn.net/lkj345/article/details/80878128

unity3d 点到向量的距离算法（方法描述ok，但是求解两侧位置不如向量法直接）：https://blog.csdn.net/qq_40795166/article/details/100030169

点到线段的最短距离：https://blog.csdn.net/angelazy/article/details/38489293