KK's Reconstruction

最新推荐文章于 2025-04-04 00:30:00 发布

qiuxueming_csdn

最新推荐文章于 2025-04-04 00:30:00 发布

阅读量600

点赞数

分类专栏：最小生成树文章标签：最小生成树

本文链接：https://blog.csdn.net/qiuxueming_csdn/article/details/53363507

版权

最小生成树专栏收录该内容

2 篇文章

订阅专栏

Description

Our lovely KK has a difficult Social problem.

A big earthquake happened in his area.

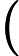
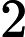
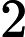
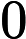
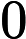
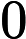
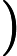
cities have been implicated. All the roads between them are destroyed.

Now KK was commissioned to rebuild these roads.

However, after investigation，KK found that some roads are too damaged to rebuild.

Therefore, there are only

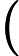
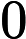
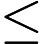
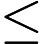
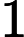
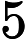
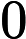
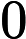
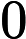
roads can be rebuilt.

KK needs to make sure that there is a way between any two cities, and KK wants to rebuild roads as few as possible.

With rebuilding minimal number of roads, he also wants to minimize the difference between the price of the most expensive road been built and the cheapest one.

Input

The first line of the input file contains an integer

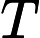
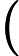
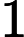
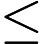
, which indicates the number of test cases.

For each test case,The first line includes two integers

，

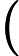
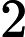
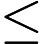
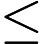
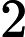
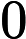
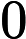
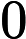
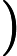
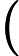
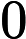
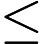
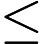
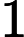
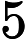
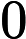
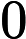
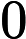
The next

lines include three integers

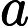
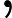
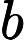
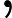
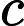
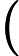
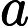
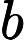
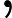
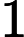
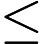
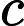
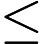
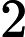
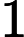
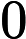
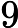
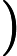
,indicating there is a undirected edge between

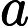
and

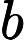
,the cost is

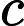
Output

For each test case, output the smallest difference between the price of the most expensive road and the cheapest one.If there is no legal solution, then output -1.

Sample Input

Sample Output

题意：有N个城市，M 条路，让你去找路使得所有的城市都连通，并且求所找的路使得最大的边和最小的边的差值最小

思路：这种保证连通集的用最小生成树（主要是连通所有的结点，求的最小的花费），这里使用kruskal()写法，基于并查集的写法，此外还有一种prim()基于最短路迪杰斯特拉的写法。我们来枚举最小的边，让其构成连通，利用 kruskal()得到最大的边，然后最小的差值。

AC代码：

#include <iostream>
#include <map>
#include <vector>
#include <cstdio>
#include <queue>
#include <algorithm>

using namespace std;

const int MAX_N = 2005;
const int INF = 0x7fffffff;

struct point {
    int s;
    int e;
    int val;
    bool operator < (const point &b) const {
        return val < b.val;
    }
} p[15005];
int fa[MAX_N];
int n,m;
int flag;

int found(int x) {
    return x == fa[x]?x:fa[x]=found(fa[x]);
}

int kruscal(int k) {
    int maxcost = 0;
    for(int i = 0;i <= n;i++){
        fa[i] = i;
    }
    int t = n;
    for(int i = k; i < m; i++) {
        int fx = found(p[i].s);
        int fy = found(p[i].e);
        if(fx != fy) {
            fa[fx] = fy;
            t--;
            maxcost = max(maxcost,p[i].val);
        }
    }
    return t==1?maxcost:0;
}

int main() {
    int t;
    scanf("%d",&t);
    while(t--) {
        scanf("%d%d",&n,&m);
        for(int i = 0; i < m; i++) {
            scanf("%d%d%d",&p[i].s,&p[i].e,&p[i].val);
        }
        sort(p,p+m);
        int ans = INF;
        flag = 1;
        for(int i = 0; i < m; i++) {
            int ans2 = kruscal(i);
            if(ans2 == 0){
                break;
            }
            ans = min(ans,ans2-p[i].val);
        }
        printf("%d\n",ans != INF?ans:-1);
    }
    return 0;
}