贝塞尔曲线拟合

贝塞尔曲线拟合

最近写论文，需要对数据点进行一个拟合，想起以前图形学学的贝塞尔曲线，便整理了一下。

简介（摘自百科）

贝塞尔曲线(Bézier curve)，又称贝兹曲线或贝济埃曲线，是应用于二维图形应用程序的数学曲线。一般的矢量图形软件通过它来精确画出曲线，贝兹曲线由线段与节点组成，节点是可拖动的支点，线段像可伸缩的皮筋，我们在绘图工具上看到的钢笔工具就是来做这种矢量曲线的。
贝塞尔曲线于1962，由法国工程师皮埃尔·贝塞尔（Pierre Bézier）所广泛发表，他运用贝塞尔曲线来为汽车的主体进行设计。贝塞尔曲线最初由Paul de Casteljau于1959年运用de Casteljau演算法开发，以稳定数值的方法求出贝兹曲线。

公式

线性公式

给定点P0、P1，线性贝兹曲线只是一条两点之间的直线。说白了，就是给一个t取0到1之间的值，对其进行插值，比如取t=0.3，P0（0,0），P1（1,0）这时候插值点的坐标是什么呢，显然是Pt（0.3,0），好，现在分别取t=0.1,0.2,…,0.9，那么我们就可以得到P0，P1之间的10个插值点，将插值点连起来，就是一条线，显然，t分的值越小，连起来的曲线越光滑，这条线由下式给出：

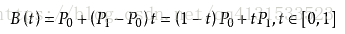
且其等同于线性插值。

二次方公式

二次方贝兹曲线的路径由给定点P0、P1、P2，其中P0，P2是数据点，也就是起点和终点，而P1是控制点，二次就不像一次那样直接线性插值就可以了，但是二次是怎么做的呢？
同样，取一个t值，在P0，P1上，用一次方的方法，得到一个点Pt1,在P1，P2上得到一个点Pt2。Pt1和Pt2之间，还是用t得到最终的Pt点，这就是二次方法，其公式如下：<