Kolmogorov Smirnov 检验

Kolmogorov-Smirnov检验

一个例子

假设你拿到下面的这100个观察值：

-0.16	-0.68	-0.32	-0.85	0.89	-2.28	0.63	0.41	0.15	0.74
1.30	-0.13	0.80	-0.75	0.28	-1.00	0.14	-1.38	-0.04	-0.25
-0.17	1.29	0.47	-1.23	0.21	-0.04	0.07	-0.08	0.32	-0.17
0.13	-1.94	0.78	0.19	-0.12	-0.19	0.76	-1.48	-0.01	0.20
-1.97	-0.37	3.08	-0.40	0.80	0.01	1.32	-0.47	2.29	-0.26
-1.52	-0.06	-1.02	1.06	0.60	1.15	1.92	-0.06	-0.19	0.67
0.29	0.58	0.02	2.18	-0.04	-0.13	-0.79	-1.28	-1.41	-0.23
0.65	-0.26	-0.17	-1.53	-1.69	-1.60	0.09	-1.11	0.30	0.71
-0.88	-0.03	0.56	-3.68	2.40	0.62	0.52	-1.25	0.85	-0.09
-0.23	-1.16	0.22	-1.68	0.50	-0.35	-0.35	-0.33	-0.24	0.25

想知道这些数据是否符合N(01)分布？

Kolmogorov-Smirnov

假设我们观察到数据,,...,,我们认为这些数据来自分布为p的数据集。

Kolmogorov-Smirnov检验的方法如下：

         : 数据来自分布为p的数据集

        否则：

        : 数据并非来自分布为p的数据集

累积分布函数与经验分布函数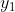

随机变量的累计分布函数(CDF)的定义大家都知道：

                                                                     

累积分布函数唯一地刻画了概率分布。

给定一个观察数列,...,，经验分布函数就是那些值不大于的概率：

                                                             

如果将观察值排序，那么:

                                                                            

我们要比较数据的经验分布函数与零假设(什么是零假设，参考 零假设 )相关的累积分布函数(所希望的CDF)。

Kolmogorov-Smirnov统计是：

                                                               

实用方法

上面例子中的数据排序后，如下表所示：

                                    

然后计算经验分布函数：

                                  ，，....，

如果数据已排序，是最小值，是最大值，那么在这个例子里就有：

                                                                       

在这里，我们假设期望的分布函数是标准正态的，所以使用正态表。下表就是标准分布的已排序的数据表：

                               

对于每一个观察值计算。

计算两个表中各项之间的绝对差值。

                              

Kolmogorov Smirnov统计＝0.092是(蓝色显示)最大值。

Kolmogorov Smirnov统计

我们计算了预期和观测分布函数之间的最大绝对距离，下图用绿色线条表示。

                                   

临界值

在95%级别下，临界值近似：

                                                                               

在这个例子中，由于n=100，因此。

由于0.092<0.136，因此我们接受零假设。

临界值可以按照下表查询(表内第一行0.20,0.15,0.10,0.05,0.01即表示80%,85%,90%,95%,99%的显著性级别）：

两个样本的Kolmogorow-Smirnov

给定两个样本，测试它们的分布是否相同。计算观测到的两个样本的累积分布函数，并计算它们的最大差值。

X : 1:2; 1:4; 1:9; 3:7; 4:4; 4:8; 9:7; 17:3; 21:1; 28:4
Y : 5:6; 6:5; 6:6; 6:9; 9:2; 10:4; 10:6; 19:3

我们对组合样本进行排序，以计算经验CDF：

                                              

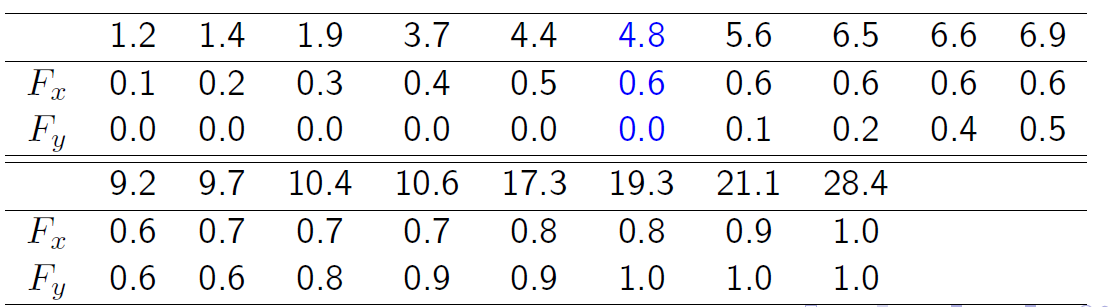
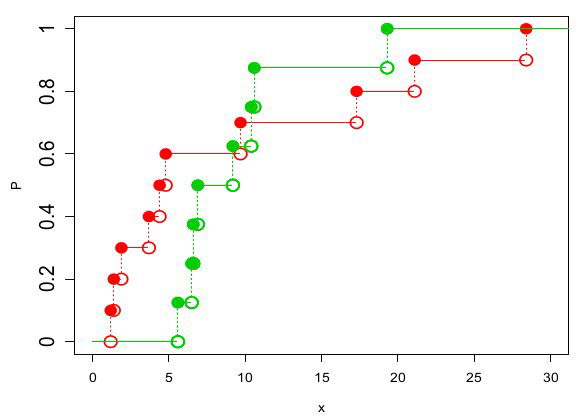Kolmogorov Smirnov统计又是两个观测分布函数的最大绝对差。在这里:

                                                                                       

对于两个样本，95%临界值可以用公式来近似：

                                                                       

在我们的例子里，，，因此。

因此我们接受零假设。