洛谷 P3811 【模板】乘法逆元

---

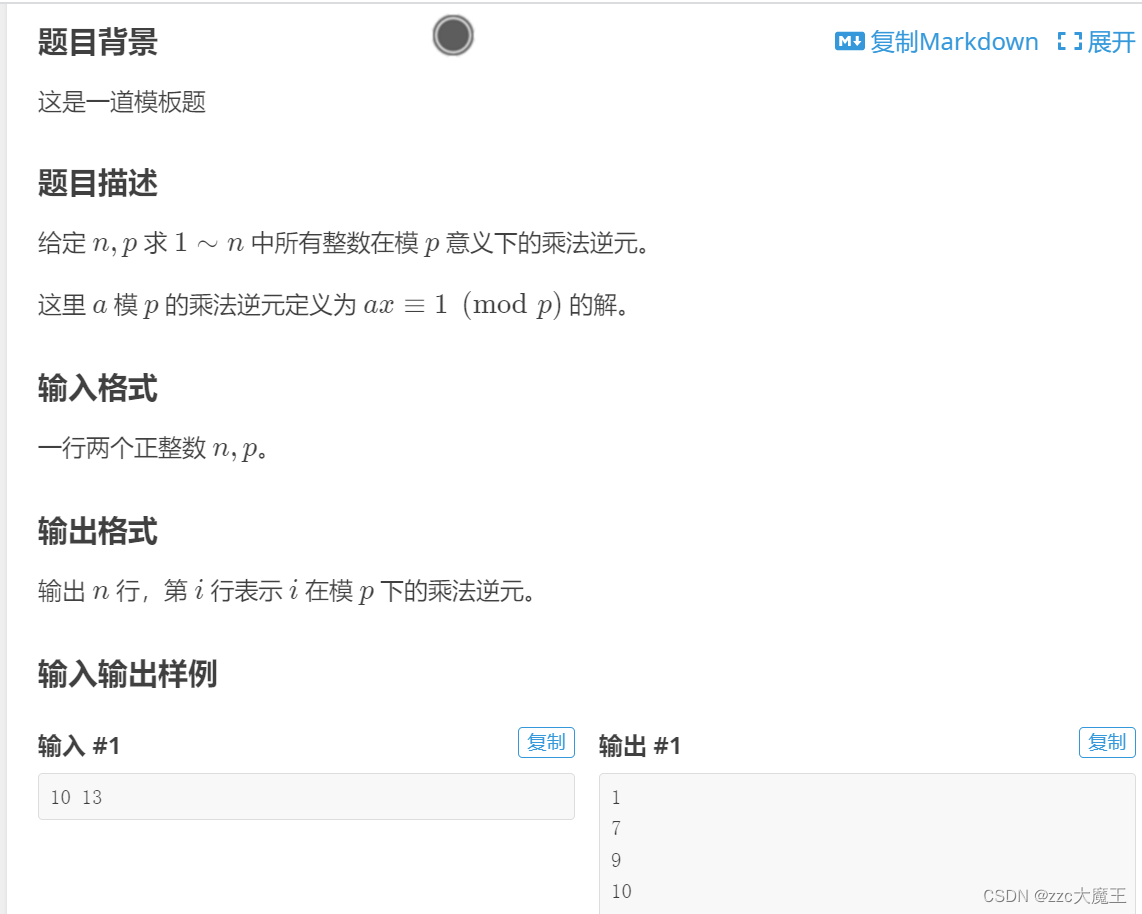
逆元定义：逆元素_百度百科

乘法逆元定义：乘法逆元_百度百科 

乘法逆元：若 a * b == 1 那么称 b是a的乘法逆元 或者 a是b的乘法逆元。

下面a，b，p皆为正整数，因为除法无法进行模运算。

设有（a / b）%p==（a%p/b%p）%p 任意代入a，b，p的值会发现这是错误的，故除法不满足取模分配律。因为分数对任意正整数取模必然是自身（无意义） 。

模意义下的乘法逆元：若 （a * b）mod p == 1 那么称 a是b模p意义下的乘法逆元 或者 b是a模p意义下的乘法逆元。

即：1/b mod p 无意义 因此以 b mod p的逆元来表达。

若要求出 a/b mod p 可以先求出 b 在模p意义下的逆元，再乘以a 整体mod p 就是这个分数的模。

同余方程含义：a * b ≡ 1（mod p），a*b mod p == 1 mod p，两边的整数取模之后相等。（此处中间的三个横线讨论的是同余符号，不是恒等符号），其中要求a与p互质，若不互质b不一定有解。

互质和质数没有必然联系，如果两个数的公因数只有1，那么称其互质。

---

再反过来看这道题，求出i在模p下的乘法逆元。设其乘法逆元为x，

若满足（x * i）% p == 1 则x为i在模p意义下的乘法逆元。

表达好一点就是 x * i ≡ 1（mod p）

因为都是正整数，所以x可以从1开始穷举，规定逆元具有唯一性，所以取最小的x。

TL代码（32分）

#include <bits/stdc++.h>
using namespace std;

int n,p;
int inverseElem(int x){
    for(int i=1;;i++){
        if((i*x)%p==1){
            return i;
        }
    }
}

int main(){
    cin.tie(nullptr),cout.tie(nullptr);
    ios::sync_with_stdio(false);
    cin>>n>>p;

    for(int i=1;i<=n;i++){//求出i在模p意义下的乘法逆元
        cout<<inverseElem(i)<<endl;
    }
    return 0;
}

超时之后只能想办法对原方程进行修改（毕竟还不会别的

例如：a % p = 1 等价于 a - p*y = 1 负号藏在y里面即 a + p*y = 1（求余数部分可以变成减去整除部分）

同样的，对于 a*x ≡ 1（mod p）也有等价式 a*x + p*y = 1

那么原来的求同余方程的解就变成了求这个不定方程的解。

因为题目给定 p 必定为质数，那么必然有 gcd（a，p）= 1

gcd【Greatest Common Divisor】即 最大公因数 或 最大公约数

使用辗转相除法(欧几里得算法)可以快速求得两个非负整数的gcd。

验证欧几里得算法的正确性：欧几里得算法_百度百科 （验证时候用到的符号 | 不是按位与的意思，是数学符号，如：5 | 30 意为 5能整除30 或者 30能被5整除，相当于5分之三十横着写）

即解不定方程 a*x + b*y = gcd（a，b）【此处b就是p，已知a，b，求一组x，y的解，x为需要的逆元】

这个形式和Exgcd（扩展欧几里得）一样，所以可以用Exgcd来求解，三言两语讲不完

传送门：【模板】二元一次不定方程 (exgcd) - 洛谷，直接看题解学！

tnnd，这道题是黄的，Exgcd是绿的，还有没有天理了。

但是要学会Exgcd的前置知识点是裴蜀[péi shǔ]定理

传送门：【模板】裴蜀定理 - 洛谷

当然这道题是有其他解法的，比如：费马小定理，欧拉定理，线性递推等等。

裴蜀定理内容：

对任何整数a、b和它们的最大公约数d，关于未知数x和y的线性不定方程（称为裴蜀等式）：若a,b是整数,且gcd(a,b)=d，那么对于任意的整数x,y,ax+by都一定是d的倍数，特别地，一定存在整数x,y，使ax+by=d成立。 ——百度百科

根据定理可得满足上述条件时（ax+by）必然是 d 的整数倍，如果不是倍数则无解。

即 ax+by = k*gcd(a,b)

取k=1，那么显然 ax+by 的最小非负值为 gcd(a,b)

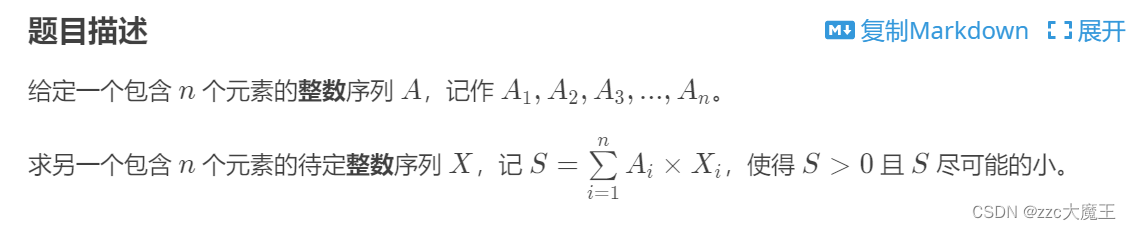
那么对于这道题来说就可以认为A1*X1 + A2*X2 是 ax+by=gcd(a,b) ，即A1*X1 + A2*X2的最小值为gcd（A1，A2），那么A1*X1 + A2*X2 + A3*X3的最小值就是gcd（A1，A2)+A3*X3 的最小值就是gcd（gcd（A1，A2），A3）。什么逆天递归

扩展欧几里得算法（Exgcd）：

对于不完全为 0 的整数 a，b，gcd（a，b）表示 a，b 的最大公约数。那么一定存在整

数 x，y 使得 gcd（a，b）=ax+by。 ——百度百科

裴蜀定理并没有给出具体求出x，y的方案，所以要学习扩欧。当裴蜀定理中的k=1时不难发现其满足Exgcd的形式，所以可以使用Exgcd来求出x，y的一组特解。

接上文，只要求出了x，y的解，那么x就是我们需要的逆元，通过解决一道绿题我们就可以拿下一道黄题。

引自神犇的证明过程：基础数论复习 - zjp_shadow - 博客园

TLE代码（64分）

#include <bits/stdc++.h>
using namespace std;
using ll = long long;

int n,p;

void exgcd(ll a,ll b,ll &x,ll &y){
    if(b==0)x=1,y=0;
    else exgcd(b,a%b,y,x),y-=a/b*x;
}

int main(){
    cin.tie(nullptr),cout.tie(nullptr);
    ios::sync_with_stdio(false);
    cin>>n>>p;
    for(int i=1;i<=n;i++){
        ll x,y;
        exgcd(i,p,x,y);
        cout<<(x%p+p)%p<<endl;//如果x为负数可以变成最小正整数
    }
    return 0;
}

有些云里雾里的那个取正整数的地方，好多地方都是公式推理和验证定理的正确性，看不懂，初等数论再说！

题解：登录 - 洛谷，详见线性递推公式。

AC代码

#include <bits/stdc++.h>
using namespace std;
using ll = long long;

int n,p;
ll inv[20000528];

int main(){
    scanf("%d %d",&n,&p);
    inv[1]=1;//1的逆元是1
    printf("%ld\n",inv[1]);
    for(int i=2;i<=n;i++){
        inv[i]=(p-p/i)*inv[p%i]%p;
        printf("%ld\n",inv[i]);
    }
    return 0;
}

事实证明下面两行代码提高cin和cout后的速度依然比不过scanf和printf

cin.tie(nullptr),cout.tie(nullptr);
ios::sync_with_stdio(false);

数据范围大的话还是老老实实用scanf和printf吧