梯度下降可视化
前一篇看完了理论,我们来实战一下,首先看一下梯度下降的效果
先看代码
# 目标函数
def func(x):
return np.square(x)
# 目标函数一阶导数
def dfunc(x):
return 2 * x
def GD_momentum(x_start, df, epochs, lr, momentum):
xs = np.zeros(epochs+1)
x = x_start
xs[0] = x
v = 0
for i in range(epochs):
dx = df(x)
v = -dx * lr + momentum * v # 计算w需要更新的值
x += v
xs.append(x) # 把新的x存储下来
return xs上面的代码就是首先定义了一个目标函数,然后定义了目标函数的一阶导数,最后我们利用梯度下降算法更新参数,并把每次新的参数存储起来,已被画图,最终的结果就是如下所示:
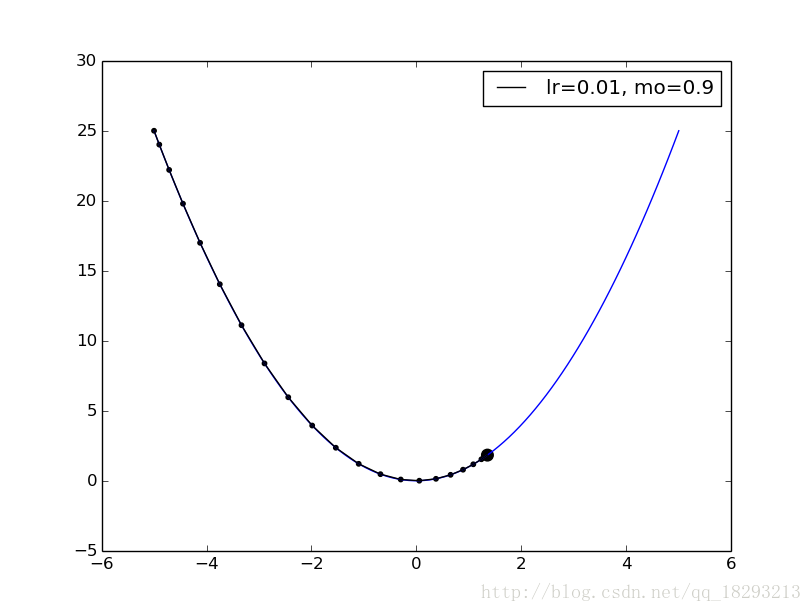
我们可以看到新的参数取值是逐渐趋向于使目标函数最小化。看完了梯度下降,我们来做做一个二分类的小实验。首先我们看一下数据,
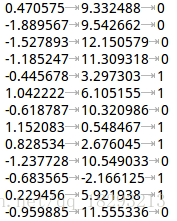
前两列是特征,第三列是label,每一行就是一个样本。
首先我们看一下数据的分布。
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
np.random.seed(1234)
# 加载数据
def loaddata():
dataMat = []
labelMat = []
for line in open('./data.txt', 'r'):
line = line.strip().split()
dataMat.append([1.0, float(line[0]), float(line[1])])
labelMat.append(int(line[2]))
return dataMat, labelMat
# 显示散点图
def plotDataSet():
data, label = loaddata()
data = np.array(data)
xcord1 = []
ycord1 = []
xcord2 = []
ycord2 = []
for i in range(data.shape[0]):
if int(label[i]) == 1:
xcord1.append(data[i, 1])
ycord1.append(data[i, 2])
else:
xcord2.append(data[i, 1])
ycord2.append(data[i, 2])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord1, ycord1, s = 20, c = 'red', marker='s', alpha = 0.5)
ax.scatter(xcord2, ycord2, s = 20, c = 'green', alpha = 0.5)
plt.title('DataSet')
plt.xlabel('X1')
plt.ylabel('Y1')
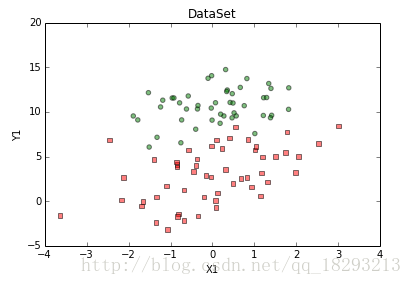
plt.show()我们看一下数据的分布,如图所示:
从图上可以看出,数据的分布很明显,可以很轻松的分开。我们需要一个 z=w1∗x1+w2∗x2+w3∗x3 来表示这个分割线,三个参数就可以搞定,我们在读入数据的时候把 x0 设为1,那 w1 就相当于b了。我们采用梯度下降算法来获得最佳的参数,
def sigmoid(inX):
return 1.0 / (1 + np.exp(-inX))
def gradAscent(data, label):
data = np.mat(data)
label = np.mat(label).transpose()
alpha = 0.0001
maxEpoch = 700
m, n = np.shape(data)
weights = np.ones((n, 1))
for i in range(maxEpoch):
h = sigmoid(data * weights)
error = -(label - h)
weights = weights - alpha * data.transpose() * error
return weights.getA()
# 绘制结果
def plotBestFit(weights):
dataMat, labelMat = loaddata()
dataArr = np.array(dataMat)
n = np.shape(dataMat)[0]
xcord1 = []; ycord1 = []
xcord2 = []; ycord2 = []
for i in range(n):
if int(labelMat[i]) == 1:
xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])
else:
xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord1, ycord1, s = 20, c = 'red', marker = 's',alpha=.5)
ax.scatter(xcord2, ycord2, s = 20, c = 'green',alpha=.5)
x = np.arange(-3.0, 3.0, 0.1)
y = (-weights[0] - weights[1] * x) / weights[2]
ax.plot(x, y)
plt.title('BestFit')
plt.xlabel('X1'); plt.ylabel('X2')
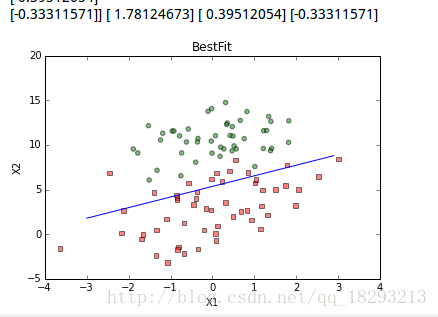
plt.show() 根据我们求出的参数,划出分割界限:
参考:
https://zhuanlan.zhihu.com/p/28922957
《统计学习方法》
























 731
731

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








