三角函数与反三角函数的拓展

三角函数

三角函数分为:
:$$\begin{gathered} \sin x,\cos x,\tan x \\ \csc x,\sec x,\cot x \end{gathered}$$
它们分别叫做正弦、余弦、正切，余割、正割、余切。
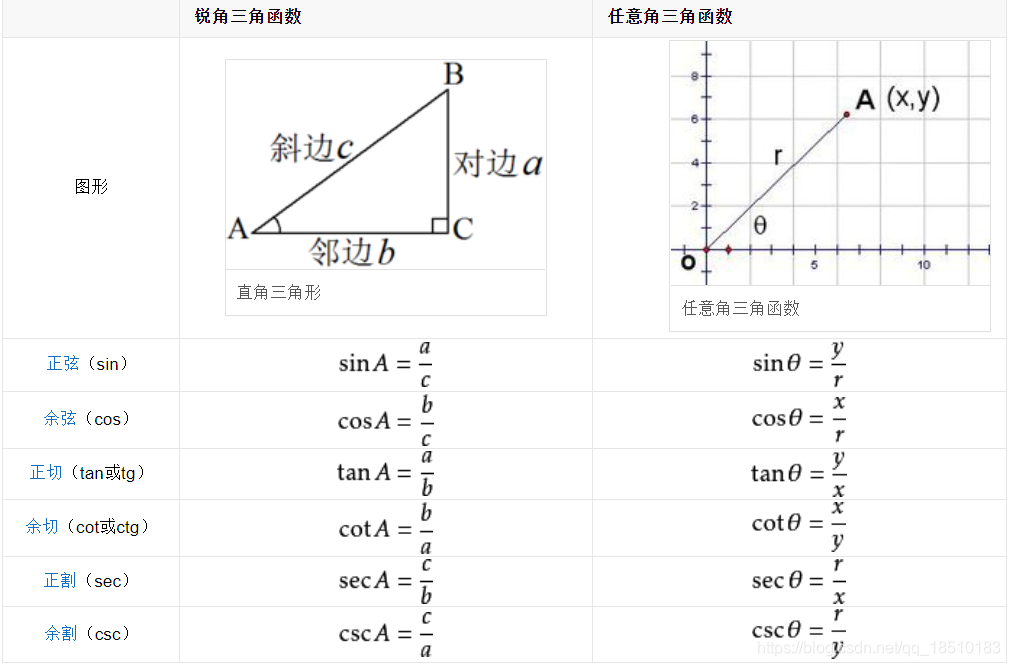
三角函数的定义出自三角形某两边之比(单位圆也可给出定义),如图1-1:

csc x,余割

• $\csc x=\frac{1}{\sin x}$

图像:

• 定义域:, { x ∣ x ≠ k π ， k ∈ Z } \{x|x≠kπ，k∈Z\} { x∣x​=kπ，k∈Z}

• 值域: { y ∣ y ≤ − 1 或 y ≥ 1 } \{y|y≤-1或y≥1\} { y∣y≤−1或y≥1}

• 渐近线:x=kπ ，k∈Z

• 有界性: |cscx|≥1,显然无界

• 奇偶性:奇函数

• 周期性:2π

• 单调性:
  $增区间:[2k\pi +$