第10章:有向图和偏序
有向图提供了一种便捷的手段来表示事物是如何相连接的,以及如何沿着连接从一个事物转移到另一个事物。它们通常被绘制为一堆点或圆,并且某些点之间存在着箭头,如图10.1所示。这些点称为节点或顶点,这些线称为有向边或箭头。

定义10.0.1:一个有向图G包含有非空集合V(G),称为G的顶点,集合E(G)称为G的边。
一条有向边所开始的顶点u称作边的尾,边所结束的顶点v称作边的头。这样的边可以通过有序对(u, v)来表示。符号(u→v)用来作为边的表示。

形式上,有向图G与集合上的二元关系相同,V=V(G),也就是说,一个有向图就是一个二元关系,它的定义域和陪域都是集合V。实际上,我们已经将关系G中的箭头称为G的“图”。
10.1 顶点的度
有向图中顶点的入度是指到达该顶点的箭头的个数,出度是指从该顶点发出的箭头的个数。
定义10.1.1:如果G是一个有向图,且v ∈V(G),那么
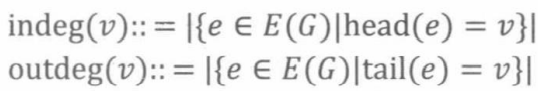
引理 10.1.2:
入度、出度的和都等于|E(G)|。
10.2 路和通路
定义10.2.1:有向图中的路是一个顶点和边交替构成的序列,始于顶点并终于顶点,对于路中的每一条边(u→v),顶点u是该边之前的一个元素,顶点v是该边之后的下一个元素。所以一条路v是一个如下形式的序列:

其中(
v
i
v_i
vi→
v
i
+
1
v_{i+1}
vi+1) ∈ E(G), i ∈ [0…k)。这条路可描述为开始于
v
i
v_i
vi,结束于
v
k
v_k
vk
且该条路的长度|V|定义为k。
路可成为一条通路,当且仅当所有的 v i v_i vi都是不同的,即,如果i ≠j,那么 v i v_i vi≠ v j v_j vj。
回路是指出发和结束都在同一个顶点的路。一个圈是一个除了起始和终止的顶点之外,所有顶点都不重复的长度为正的回路。
一个单一节点可当作一个长度为零的通路,起始并终止于它自身。并且,它还是一个回路,但是不能算作一个圈,因为根据定义要求,圈的长度必须为正。
路的合并:如果一条路f结束于顶点v,且路r开始于同一顶点v,那么我们说它们的合并f^r是一条从f开始并延续到r的路。我们将用符号 f v ^ r f\widehat{v}r fv r来表述终点为v的路f和起点为v的路r合并。
引理 10.2.1:

10.2.1 查找通路
定理10.2.3 :从一个顶点到另一个顶点最短的路是一条通路。(良序原理+反证法证明)
定义10.2.4:一个图中顶点u到顶点v的距离,dist(u, v),是从u到v最短通路的长度。
引理10.2.5:「三角不等式]对于所有的顶点u, v,x ,
d
i
s
t
(
u
,
v
)
≤
d
i
s
t
(
u
,
x
)
+
d
i
s
t
(
x
,
v
)
dist(u,v){\leq}dist(u,x)+dist(x,v)
dist(u,v)≤dist(u,x)+dist(x,v)
证明:为了证明这一不等式,设f是一个从u到x的最短通路,且r是从x到v的最短通路。那么依据引理10.2.2,
f
x
^
r
f \widehat{x} r
fx
r是一条从u到v长度为dist(u,x ) + dist(x,v)的路,因此根据定理10.2.3,这个和是从u到v最短通路长度的上界。
引理10.2.6:经过一个顶点的最短正长度的回路就是经过该顶点的一个圈。
10.3 邻接矩阵
如果一个图G有n个顶点 v 0 , v 1 . . . , v n − 1 v_0, v_1...,v_{n-1} v0,v1...,vn−1,那么对其进行表示的有效方法是用一个n × n的零一矩阵,称为该图的邻接矩阵 A G A_G AG。如果从顶点 v i v_i vi到顶点 v j v_j vj存在一余边,那么邻接矩阵的第ij个元素, ( A G ) i j (A_G)_{ij} (AG)ij,取值为1,否则取值为0。也就是,

这种表达的一个好处是,我们可以利用矩阵的幂来计算顶点之间路的条数。
更一般地说,矩阵 ( A G ) k (A_G)^k (AG)k提供了任意有向图G中顶点之间长度为k的路的条数
定义10.3.1:一个有n个顶点的图G,其中长度为k(也称为k长度)的路(walk)的计数矩阵是一个n ×n的矩阵C

定理10.3.2:如果C是图G的k长度路的计数矩阵,且D是m长度路的计数矩阵,那么CD是图G的k+m长度路的计数矩阵。
根据以上的两个定理,可有如下的推论:
推论10.3.3 :有向图G的k长度计数矩阵为 ( A G ) k (A_G)^k (AG)k,k ∈ N。
10.3.1 最短路径
在一个n顶点的图G中找到所有最短路径的一个简单方法是一个接一个地对 A G A_G AG做连续的幂计算,直到第n -1次,观察使得每一个元素首次变为正值的幂计算。这是因为定理10.3.2揭示了,如果u到v之间存在最短路径,那么它的长度(也就是u和v之间的距离)就是使 ( A G ) u v k (A_G)_{uv}^k (AG)uvk非零的最小的k。并且如果存在最短路径,它的长度会小于或等于n -1。对这一想法的改进可以给出查找最短路径的合理有效的方法。这些方法同样可以应用于加权图。加权图上的边被标注了
10.4 路关系
有向图中的一个基本问题是,是否存在从一个特定的顶点到另一个顶点的一条路径。所以,对于任意的有向图G,我们感兴趣的是一个二值关系G*称作V(G)上的路关系,其中

类似地,存在正路关系
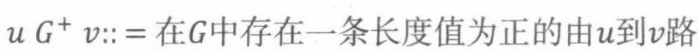
定义10.4.1:font>当由顶点v到顶点w存在一条路时,我们说w是由v可达的,或者等价的说法是,v到w是连通的。
10.4.1 复合关系
定义10.4.2:令R:B →C且S:A →B为二值关系。那么R和S的复合为二值关系(R · S):A →C,由如下规则定义

我们用 G n G^n Gn表示G与自己的n次复合,那么就很容易检验 G n G^n Gn就是n长度的路关系:
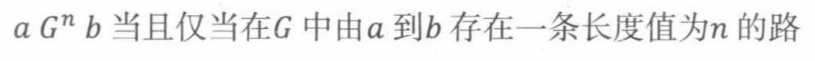

10.5 有向无环图&调度
定义10.5.1:有向无环图(DAG)是不包含圈的有向图。
DAG在计算机科学中尤其重要。它们捕获了用于分析任务调度和并发控制的关键概念。当在多个处理器上进行程序分发时,如果程序的某部分所需要的来自另一个部分的输出还没完成,我们就会遇到麻烦。
10.5.1 调度
在一个调度问题中,有一个任务集合,和一个约束集合,用于说明启动某个任务所需要事先完成的其他任务。我们可以把这些集合映射到有向图中,以任务为节点,直接先决约束作为边。
定义10.5.2:有限 DAG 的拓扑排序是一个所有顶点的列表,使得每个顶点v在列表中的出现早于其他每一个由v可达的顶点。
有限DAG 拓扑排序可以很容易地从极小元素开始构造出来。
定义10.5.3: DAG D中的一个顶点v是最小的,当且仅当每个其他的顶点都是由v可达的。顶点v为极小的,当且仅当v从任何顶点都不可达。
一个DAG可能没有最小元素,但是有很多极小元素。
定理10.5.4:每一个有限DAG都有拓扑排序。
10.5.2 并行任务调度
对于任务依赖,拓扑排序提供了一种遵守依赖关系的同时逐个执行任务的方法。但是如果我们具有在同一时刻执行多于一个任务的能力呢?
例:
在第一个时间单元,我们应该做所有的极小项,所以我们会穿上左袜子、右袜子、内衣和衬衣。在第二个时间单元,应该穿裤子和打领带。注意,还不能穿上左脚或右脚的鞋,因为还没有穿上裤子。在第三个时间单元,我们应该穿上左脚鞋子、右脚鞋子、系上腰带。在最后的时间单元中,我们可以穿上外套。这个调度如图10.9所示。
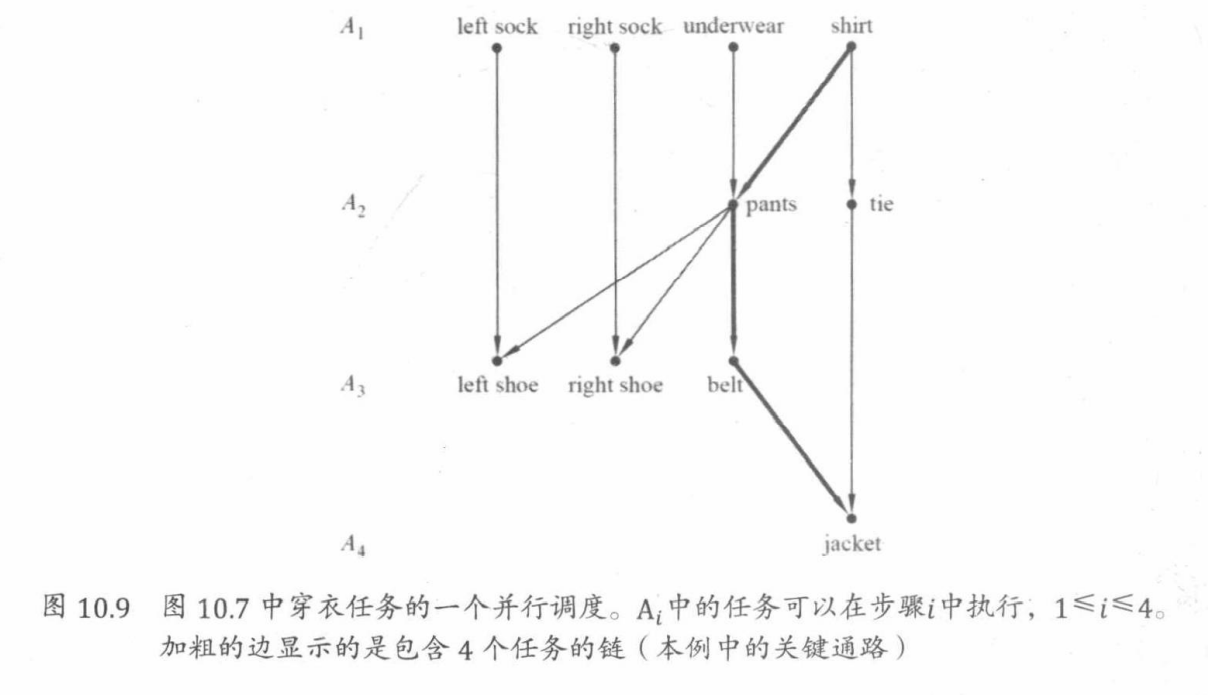
定义10.5.5 :DAG 中的两个顶点是可比较的,当其中一个是从另一个可达的。DAG 中的一个链是一个顶点的集合,使得其中任意两个顶点都是可比较的。由链中的所有其他顶点均可达的顶点是该链的最大元素。一个有限的链结束于它的最大元素。
当处理器个数不限的时候,调度任务所花费的时间至少也要和任意链中的顶点个数一样多。因此,最大的链也称作关键通路。
定义10.5.6:集合A的划分( partition)是A的非空子集的集合这些非空子集被称作划分的块( block ) ———使得A中的每个元素都恰好在一个块中。

定义10.5.7:对于DAG D的一个并行调度是对V(D)的一个划分,得到块 A 0 A_0 A0, A 1 A_1 A1…,使得当j<k时,A,中的任意顶点到A,中的任意顶点都是不可达的。块 A k A_k Ak称作调度步骤k的元素集合,且调度的时间是块的个数。任意调度步骤上的最大元素个数称为调度所需的处理器个数。
定理10.5.8: 有限 DAG D的最短时间调度包含集合
A
0
A_0
A0,
A
1
A_1
A1…,其中
A
k
A_k
Ak:: ={a
∈
\in
∈ V(D) | depth(a)= k}
推论10.5.9:并行时间=关键通路的大小。当处理器的个数是有界的时候,情况会更加复杂一些。
10.5.3 Dilworth引理
定义10.5.10 :DAG中的一个反链是一个不存在可比较的两个元素的顶点集合——集合中任意两个不同的顶点之间不存在路。
推论10.5.11: 在 DAG D中,如果最大链的大小为t,那么V(D)可以被划分为t个反链。
引理10.5.12 :( Dilworth )对于所有的t >0,每个有n个顶点的DAG要么有一个大于t的链,要么有一个大小至少为n/t的反链。
证明:假设没有大小大于t的链。令t为最大反链的大小。如果根据推论10.5.11的证明来制订并行调度,建一些和最大链一样大小的反链,它们的数量小于等于t。每个元素只属于一个反链,每个反链都不大于t。所以总的元素个数最多为乘以t,也就是,t≥n。应用简单的除法可得到l≥n/t。
推论10.5.13:每一个有n个顶点的DAG都有长度大于 n \sqrt{n} n的链或者长度至少为 n \sqrt{n} n的反链。
10.6 偏序
在本章的引言中,我们提及了一个有用的事实,在此值得再次强调:形式化地说,任何有向图都等同于二值关系,它的域和陪域都是其顶点。这意味着任何域和陪域相同的二值关系都可以变换成有向图!
10.6.1 DAG中路关系的性质
定义10.6.1:集合A上的关系R是传递的 ( transitive ),当且仅当对于每个a,b, c ∈ A,有 (a R b AND b R c) =a R c
因此我们有
引理10.6.2:对任意有向图G,路关系 G + G^+ G+和 G ∗ G^* G∗是传递的。
由于每个顶点都有一个长度为零的路通往自身,路关系还有另一个关系性质,称作自反性。
定义10.6.3:集合A上的一个二值关系R是自反的( reflexive ),当且仅当对于所有的a ∈ A有a R a。
现在我们有
引理10.6.4:对于任意有向图G、路关系G*是自反的。
我们知道,当且仅当一个有向图没有长度为正的回路时,这个有向图为 DAG。既然回路上的任意顶点可以作为路的起点和终点,说一个图是DAG等同于说图中任何顶点都没有返回到自身的正长度通路。这意味着,DAG的正的路关系D+具有称为非自反的性质。
定义10.6.5:集合A上的二值关系R是非自反的,当且仅当对于所有的a ∈ A有 NOT(a R a)
引理10.6.6:R是一个DAG,当且仅当R+是非自反的
10.6.2 严格偏序
定义10.6.7:具有传递性的且非自反的关系称作严格偏序关系。
定理10.6.8: 关系R是严格偏序关系,当且仅当R是一个DAG中的正路关系。
例:
定义10.6.9:集合A上的二值关系R是非对称的,当且仅当对于所有的a, b ∈ A

推论10.6.10: 有向图D是一个DAG,当且仅当D+是非对称的。
推论10.6.10和定理10.6.8相结合可得出以下推论。
推论10.6.11:集合A上的二值关系R是严格偏序关系,当且仅当它是传递的和非对称的。
10.6.3 弱偏序
弱偏序:就是在严格偏序上增加每个元素都与自身相关的附加条件。如需更精确地阐述,我们要放松非对称属性,使之不适用于顶点与自身的比较,这个放松性质称作反对称性。
定义10.6.12:集合A上的二值关系R是反对称的,当且仅当对于所有的a ≠ b E A

定义10.6.13:一个集合上的一个二值关系是弱偏序,当且仅当它是传递的、自反的和反对称的。
根据这个定义,下面的引理给出了弱偏序的另外一个描述。
引理10.6.14:集合A上的关系R是弱偏序,当且仅当A上的严格偏序S使得对于所有的a, b ∈ A,有

推论10.6.15:一个关系是弱偏序,当且仅当该关系是一个DAG的路关系。

10.7 用集合包含表示偏序
在这一节中,我们会介绍每个偏序可以用由包含关系联系在一起的一个集合族来描绘。也就是说,每个偏序都与这样的由集合构成的族具有“相同形状”。与“相同形状”对应的技术性词汇是“同构”。
定义10.7.1:集合A上的二进制关系R与集合B上的关系S是同构的
当且仅当存在由A到B的关系保持的双射。也就是说,存在一个双射f:A →B使得对于所有的a, a’
∈
\in
∈ A,



10.8 线性序
为人熟知的数字的序关系还有一个重要的附加性质:给定两个不同的数字,其中一个要大于另外一个,具有这种性质的偏序称作线性序。
定义10.8.1:令R为集合A上的二元关系,令a,b为A中的元素。那么a和b关于R是可比较的,当且仅当[a R b OR b R a]。每两个不同元素都是可比较的偏序称作线性序。
10.9 乘积序
取两个关系的乘积是从旧的关系创建新的关系的一种有效办法。

从定义可知,乘积保持了传递、自反、非自反,以及反对称性质(参见习题10.50 )。如果 R 1 R_1 R1和 R 2 R_2 R2,都具有这些性质之一,那么 R 1 × R 2 R_1×R_2 R1×R2同样也具有该性质。这暗示了如果 R 1 R_1 R1和 R 2 R_2 R2都是偏序,那么 R 1 × R 2 R_1×R_2 R1×R2同样也是。
10.10 等价关系
定义10.10.1:如果一个关系是自反的、对称的以及可传递的,那么这个关系是一个等价关系。

任何全函数在它定义域上定义了一个等价关系:
全函数:处处有定义的函数。
定义10.10.2:
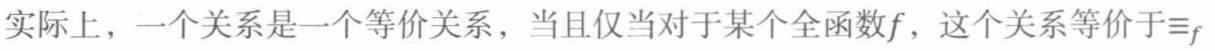
10.10.1 等价类
等价关系与划分有密切的联系,因为等价关系下的元素的像就是划分得到的块。
定义10.10.3:给定一个等价关系R:A →A,元素a∈ A的等价类 [ a ] R [a]_R [a]R是A中与a以R关系相关的所有元素。即,

换言之, [ a ] R [a]_R [a]R就是像R(a)。
定理10.10.4:集合A上的等价关系的等价类是A上划分的块。
10.11 关系性质的总结
关系R:A →A与A为顶点的有向图相同。
自反性 R是自反的,当

R中的每个顶点都有一个自循环。
非自反性 R是非自反的,当

R中没有自循环。
对称性 R是对称的,当
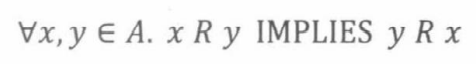
如果在R中存在由x到y的边,那么同样也存在从y回到x的边。
非对称性 R是非对称的,当
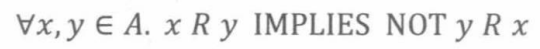
在R中的两个顶点之间最多存在一条有向边,且不存在自循环。
反对称性 R是反对称的,当

等价的,

两个不同的顶点之间至多有一条有向边,但可以存在自循环。
传递性 R是传递的,当

如果由u到v存在一条正长度通路,那么从u到v就存在一条边。
线性 R是线性的,当

给定R中的任意两个顶点,它们之间存在正向或反向的一条边。
严格偏序 R是一个严格偏序,当且仅当R是传递的和非自反的,当且仅当R是传递的和非对称的,当且仅当它是一个DAG上的正长度路关系。
弱偏序 R是一个弱偏序,当且仅当R是传递的、反对称的和自反的
当且仅当R是一个DAG上的路关系。
等价关系 R是一个等价关系,当且仅当R是自反的、对称的和传递的,当且仅当R等于domain®的某个划分中的属于同一块关系。
























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








