VASP计算二维材料的载流子迁移率（Mobility calculation notes for 2D materials using VASP code）

最新推荐文章于 2025-11-19 09:43:08 发布

转载最新推荐文章于 2025-11-19 09:43:08 发布 · 1.5k 阅读

4 ·

CC 4.0 BY-SA版权

原文链接：https://yh-phys.github.io/blog/2019/vasp-mobility/

文章标签：

#科技

VASP 专栏收录该内容

28 篇文章

订阅专栏

Mobility calculation notes for 2D materials using VASP code

前言
理论基础
计算与数据处理工具
二维InSe有效质量计算过程
二维InSe载流子迁移率计算过程
后记
- - - 参考文献

前言

载流子迁移率通常指半导体内部电子和空穴整体的运动快慢情况，是衡量半导体器件性能的重要物理量。2004年，石墨烯的成功剥离引起了研究人员对于二维材料性质探索的浓厚兴趣。石墨烯、黑磷等二维材料展现出的高载流子迁移率是其中的一个重要研究课题，科研人员在理论计算方面已经做了大量的工作。由于电子在运动过程中不仅受到外电场力的作用，还会不断的与晶格、杂质、缺陷等发生无规则的碰撞，大大增加了理论计算的难度。目前计算载流子迁移率比较常用的理论是形变势理论和玻尔兹曼输运理论，前者没有考虑电子和声子（晶格振动）以及电子与电子之间的相互作用等因素，计算结果存在一定的误差，但笔者的计算结果与实验值在数量级上是吻合的；玻尔兹曼输运理论的一种计算考虑了电子-声子的相互作用，基于第一性原理计算和最大局域化wannier函数插值方法，借助于Quantum-ESPRESSO和EPW软件可以完成载流子迁移率计算。缺点是计算量太大，一般的课题组很难承受起高昂的计算费用，另外EPW软件对于二维材料的计算存在部分问题，在其官方论坛也有讨论，计算过程在后续文章中会提到。本文以形变势理论方法为基础，详细介绍了二维InSe的电子和空穴的有效质量与载流子迁移率的计算方法。

理论基础

基于Bardeen和Shockley $^{[1]}$ 提出的形变势理论，二维材料载流子迁移率可以根据下式计算：
$\mu_{\rm 2D} = \frac{e\hbar^3C_{2D}}{k_BTm^{\ast}m_dE_1^2}$
其中， $𝑚^∗$ 是传输方向上的有效质量， $T$ 是温度， $𝑘_𝐵$ 是玻尔兹曼常数。 $𝐸 _1$ 表示沿着传输方向上位于价带顶（VBM）的空穴或聚于导带底（CBM）的电子的形变势常数，由公式 $E_1 = {\Delta}E/({\Delta}l/l_o)$ 确定， ${\Delta}E$ 为在压缩或拉伸应变下CBM或VBM 的能量变化， $𝑙_0$ 是传输方向上的晶格常数， ${\Delta}l$ 是 $𝑙_0$ 的变形量。 $𝑚_𝑑$ 是载流子的平均有效质量，由公式 $𝑚_𝑑=\sqrt{m_x^{\ast}m_y^{\ast}}$ 定义。 $𝐶_{2𝐷}$ 是均匀变形晶体的弹性模量，对于2D材料，弹性模量可以通过公式 $C_{2D}=2[{\partial}^2E/{\partial}({\Delta}l/l_0)^2]/S_0$ 来计算，其中 𝐸 是总能量， $𝑆_0$ 是优化后的面积。下面对公式中的单位（量纲）做一个简单换算，具体如下：

$𝑚_𝑑=\sqrt{m_x^{\ast}m_y^{\ast}}:(kg)$
$E_1 = {\Delta}E/({\Delta}l/l_o):(J)$ 在VASP中 ${\Delta}E$ 的单位是 $e V$ , $\times 10^{-19}J$ ,此处需要换算。
$C_{2D}=2[{\partial}^2E/{\partial}({\Delta}l/l_0)^2]/S_0:(J/m^2)$ 其中E是总能（eV）， $S_0$ 表示面积（ ${\AA}^2$ ）
$\times 10^{-19}C$
$\times 10^{-19}C$
$k_B：1.6 \times 10^{-19}C$
$m*:K_g$ 换算过程

$\begin{aligned} & \frac{\mathrm{C}\cdot\mathrm{J}^3\cdot\mathrm{s}^3\cdot\frac{\mathrm{J}}{\mathrm{m}^2}}{\frac{\mathrm{J}}{\mathrm{K}}\cdot\mathrm{K}\cdot\mathrm{k}\mathrm{g}\cdot\mathrm{k}\mathrm{g}\cdot\mathrm{J}^2}=\frac{\mathrm{C}\cdot\mathrm{J}\cdot\mathrm{s}^3}{\mathrm{m}^2\cdot\mathrm{k}\mathrm{g}^2}=\frac{\mathrm{C}\cdot\mathrm{J}}{\frac{\mathrm{m}^2\cdot\mathrm{k}\mathrm{g}^2}{\mathrm{s}^3}\cdot\frac{\mathrm{s}}{\mathrm{s}}\cdot\frac{\mathrm{m}^2}{\mathrm{m}^2}} \\ & =\frac{\mathrm{C\cdot J}}{\frac{\mathrm{s}}{\mathrm{m}^{2}}\cdot\frac{\mathrm{m}^{4}\cdot\mathrm{kg}^{2}}{\mathrm{s}^{4}}}=\frac{\mathrm{m}^{2}}{\mathrm{s}}\cdot\frac{\mathrm{C}}{\mathrm{J}} \\ & \mathrm{=m^{2}\cdot \mathrm{~s}^{-1} \cdot V^{-1}} \end{aligned}$
也可以写作： $cm^2 \cdot s^{-1}\cdot V^{-1}$
其中： $\frac{J}{C}$ , $1J=1kg\cdot m^2/s^2$

计算与数据处理工具

• VASP.5.4.4软件 (可以手动控制优化晶格方向)
• OriginLab软件
• Excel
• Materials Studio软件
• 正格矢到倒格矢转化脚本，来源于小木虫

#! /usr/bin/python
# This program reads in base vectors from a given file, calculates reciprocal vectors
# then writes to outfile in different units
# LinuxUsage: crecip.py infile outfile
# Note:  the infile must be in the form below:
#   inunit  ang/bohr
#   _begin_vectors
#     46.300000000   0.000000000   0.000000000
#      0.000000000  40.500000000   0.000000000
#      0.000000000   0.000000000  10.000000000
#   _end_vectors
# 
# Note: LATTICE VECTORS ARE SPECIFIED IN ROWS !
def GetInUnit( incontent ):
  inunit = ""
  for line in incontent:
      if line.find("inunit") == 0:
          inunit = line.split()[1]
          break
  return inunit
def GetVectors( incontent ):
  indstart = 0
  indend = 0
  for s in incontent:
      if s.find("_begin_vectors") != -1:
          indstart = incontent.index(s)
      else:
          if s.find("_end_vectors") != -1:
              indend = incontent.index(s)
  result = []
  for i in range( indstart + 1, indend ):
      line = incontent[i].split()
      result.append( [ float(line[0]), float(line[1]), float(line[2]) ] )
  return result
def Ang2Bohr( LattVecAng ):
  LattVecBohr = LattVecAng
  for i in range(0,3):
      for j in range(0,3):
          LattVecBohr[i][j] = LattVecAng[i][j] *  1.8897261246
  return LattVecBohr
def DotProduct( v1, v2 ):
  dotproduct = 0.0
  for i in range(0,3):
      dotproduct = dotproduct + v1[i] * v2[i]
  return dotproduct
def CrossProduct( v1, v2 ):
  # v3 = v1 WILL LEAD TO WRONG RESULT
  v3 = []
  v3.append( v1[1] * v2[2] - v1[2] * v2[1] )
  v3.append( v1[2] * v2[0] - v1[0] * v2[2] )
  v3.append( v1[0] * v2[1] - v1[1] * v2[0] )
  return v3
def CalcRecVectors( lattvec ):
  pi = 3.141592653589793
  a1 = lattvec[0]
  a2 = lattvec[1]
  a3 = lattvec[2]
  b1 = CrossProduct( a2, a3 )
  b2 = CrossProduct( a3, a1 )
  b3 = CrossProduct( a1, a2 )
  volume = DotProduct( a1, CrossProduct( a2, a3 ) )
  RecVec = [ b1, b2, b3 ]
  # it follows the definition for b_j: a_i * b_j = 2pi * delta(i,j)
  for i in range(0,3):
      for j in range(0,3):
          RecVec[i][j] = RecVec[i][j] * 2 * pi / volume
  return RecVec    
def main(argv = None):  
  argv = sys.argv
  infilename  = argv[1]
  outfilename = argv[2]    
  pi = 3.141592653589793
  bohr2ang = 0.5291772109253
  ang2bohr = 1.889726124546    
  infile  = open(infilename,"r")
  incontent = infile.readlines()
  infile.close()    
  inunit = GetInUnit( incontent )
  LattVectors = GetVectors( incontent )
  # convert units from ang to bohr
  if inunit == "ang":
      LattVectors = Ang2Bohr( LattVectors )    
  # calculate reciprocal vectors in 1/bohr
  RecVectors = CalcRecVectors( LattVectors )    
  # open outfile for output
  ofile = open(outfilename,"w")    
  # output lattice vectors in bohr
  ofile.write("lattice vectors in bohr:\n")
  for vi in LattVectors:
      ofile.write("%14.9f%14.9f%14.9f\n" % (vi[0], vi[1], vi[2]))
  ofile.write("\n")    
  # output lattice vectors in ang
  convfac = bohr2ang
  ofile.write("lattice vectors in ang:\n")
  for vi in LattVectors:
      ofile.write("%14.9f%14.9f%14.9f\n" % (vi[0]*convfac, vi[1]*convfac, vi[2]*convfac))
  ofile.write("\n")    
  # output reciprocal vectors in 1/bohr
  ofile.write("reciprocal vectors in 1/bohr:\n")
  for vi in RecVectors:
      ofile.write("%14.9f%14.9f%14.9f\n" % (vi[0], vi[1], vi[2]))
  ofile.write("\n")    
  # output reciprocal vectors in 1/ang
  convfac = ang2bohr
  ofile.write("reciprocal vectors in 1/ang:\n")
  for vi in RecVectors:
      ofile.write("%14.9f%14.9f%14.9f\n" % (vi[0]*convfac, vi[1]*convfac, vi[2]*convfac))
  ofile.write("\n")    
  # output reciprocal vectors in 2pi/bohr
  convfac = 1.0/(2.0*pi)
  ofile.write("reciprocal vectors in 2pi/bohr:\n")
  for vi in RecVectors:
      ofile.write("%14.9f%14.9f%14.9f\n" % (vi[0]*convfac, vi[1]*convfac, vi[2]*convfac))
  ofile.write("\n")
  # output reciprocal vectors in 2pi/ang
  convfac = ang2bohr/(2.0*pi)
  ofile.write("reciprocal vectors in 2pi/ang:\n")
  for vi in RecVectors:
      ofile.write("%14.9f%14.9f%14.9f\n" % (vi[0]*convfac, vi[1]*convfac, vi[2]*convfac))    
  # close
  ofile.close()    
  return 0
if __name__ == "__main__":
 import sys
 sys.exit(main())

二维InSe有效质量计算过程

建模

由于计算过程中需要对二维InSe施加应变，但二维InSe原胞是六角结构，不容易施加应变。但是侯柱峰老师讲了对石墨烯原胞施加应变的方法，笔者认为虽然可行，但过于繁琐，故不采用此法。我们可以利用根号建模的方法讲六角结构InSe原胞变为方形结构的InSe超胞，然后施加应变可大大提高操作效率，但计算量的增加再可接受范围之内。下面给出关键的建模步骤，更多的根号建模部分可参考我的往期博客文章。

切面并构建二维InSe原胞，同时调整晶格基矢，使其变为方形结构

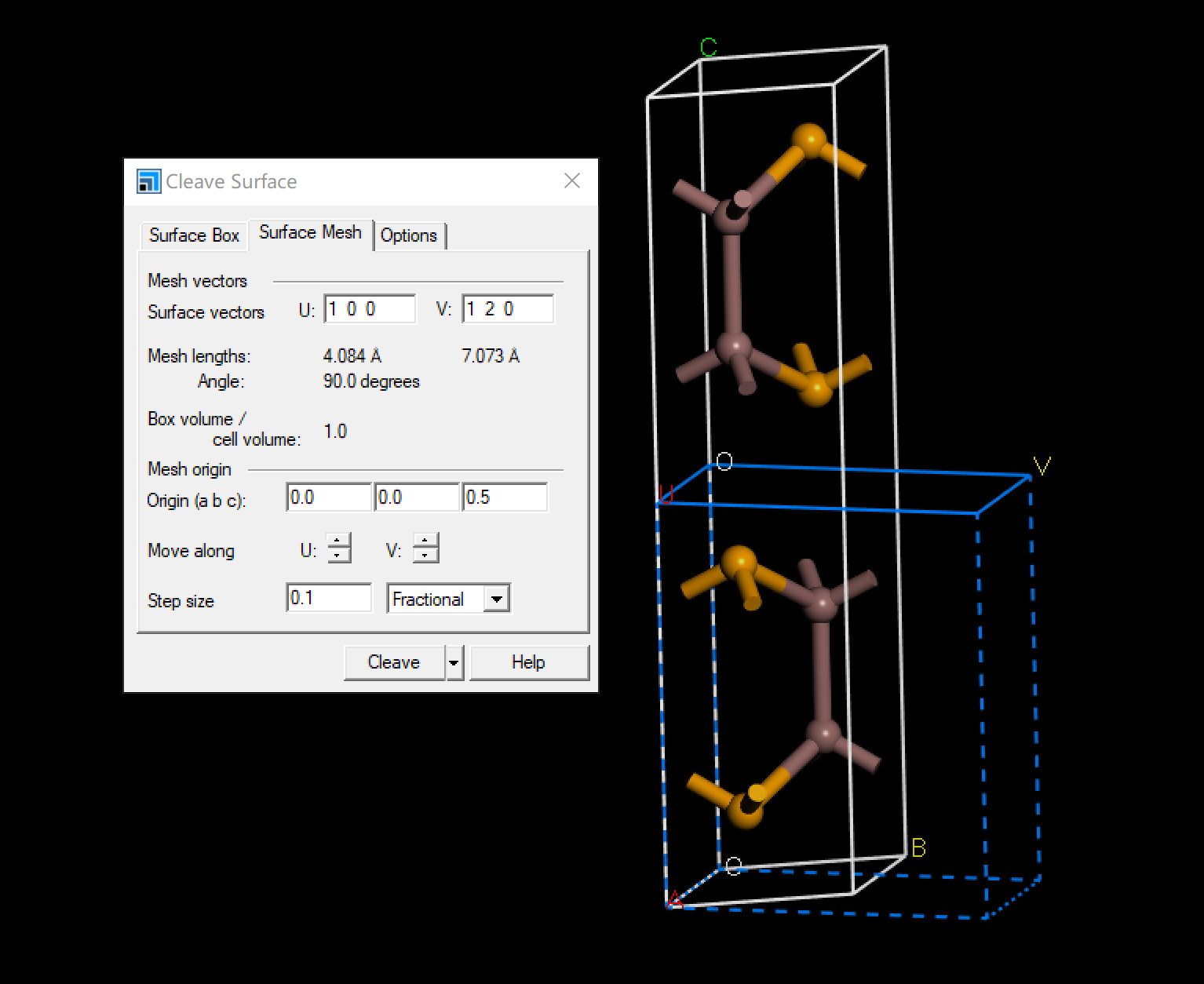
在这里插入图片描述

能带计算

结构优化

INCAR

SYSTEM = InSe             
ISTART = 0       
NWRITE = 2      
PREC   = Accurate
ENCUT  = 500
GGA    = PE      
NSW    = 200
ISIF   = 3         
ISYM   = 2        
IBRION = 2      
NELM   = 80        
EDIFF  = 1E-05         
EDIFFG = -0.01 
ALGO   = Normal            
LDIAG  = .TRUE.  
LREAL  = .FALSE.          
ISMEAR = 0         
SIGMA  = 0.05 
ICHARG = 2
LWAVE  =  .FALSE.          
LCHARG = .FALSE.
NPAR   = 4

KPOINTS

Monkhorst Pack
0
Gamma
 11   7   1
.0   .0   .0

POSCAR

Se   In
1.000
     4.083622259999999      -0.000000000000001       0.000000000000000
     0.000000000000000       7.073041233239241       0.000000000000000
     0.000000000000000       0.000000000000000      25.377516849029359
Se   In
4   4
Direct
0.5000005000000000   0.1666665000000000   0.5271404971815050   !Se
0.0000004999999997   0.6666665000000004   0.5271404971815050   !Se
0.5000005000000000   0.1666665000000000   0.3152396685456632   !Se
0.0000004999999997   0.6666665000000004   0.3152396685456632   !Se
0.4999995000000003   0.8333335000000002   0.4767849697227853   !In
-0.0000005000000000   0.3333335000000000   0.4767849697227853   !In
0.4999995000000003   0.8333335000000002   0.3655951960043828   !In
 -0.0000005000000000   0.3333335000000000   0.3655951960043828   !In

OPTCELL

100
010
000

POTCAR

cat Se/POTCAR In_d/POTCAR > POTCAR

静态自洽

INCAR
SYSTEM = InSe             
ISTART = 0       
NWRITE = 2      
PREC   = Accurate
ENCUT  = 500
GGA    = PE      
NSW    = 0
ISIF   = 2         
ISYM   = 2       
IBRION = -1      
NELM   = 80        
EDIFF  = 1E-05         
EDIFFG = -0.01 
ALGO   = Normal            
LDIAG  = .TRUE.  
LREAL  = .FALSE.          
ISMEAR = 0         
SIGMA  = 0.05 
ICHARG = 2
NPAR   = 4

KPOINTS

Monkhorst Pack
0
Gamma
 21   13   1
.0   .0   .0

POSCAR

cp CONTCAR scf/POSCAR

能带计算

INCAR

SYSTEM = InSe             
ISTART = 1       
NWRITE = 2      
PREC   = Accurate
ENCUT  = 500
GGA    = PE      
NSW    = 0
ISIF   = 2         
ISYM   = 2       
IBRION = -1      
NELM   = 80        
EDIFF  = 1E-05         
EDIFFG = -0.01 
ALGO   = Normal            
LDIAG  = .TRUE.  
LREAL  = .FALSE.          
ISMEAR = 0         
SIGMA  = 0.05 
ICHARG = 2
LORBIT = 11
LWAVE  =  .FALSE.          
LCHARG = .FALSE.
NPAR   = 4

KPOINTS

k-points along high symmetry lines
80
Line-mode
Rec
 0          0.5       0       !Y
 0          0         0       !gamma

 0          0         0       !gamma
 0.5        0         0       !X

 0.5        0         0       !X
 0.5        0.5       0       !S

 0.5        0.5       0       !S
 0          0.5       0       !Y

有效质量计算

计算说明

对于包含了晶格周期性的有效质量的表达式，表示为如下表cp ./CHGCAR ./band/达式
$\frac{1}{m^*}=\frac{1}{\hbar^2}\frac{\partial^2E(k)}{\partial k^2}$
在带入物理量进行有效质量计算时，涉及单位制问题。一般写输入文件时，长度单位为 Å；而程序输出的能带结构中，能量单位为 eV，计算起来比较繁琐。原子单位制有两种，一种为 Hartree 原子单位制，另一种为 Rydberg 单位制。这两种单位制的区别在于，Hartree 单位制下基本物理量简单，电子电荷和质量都为1；而 Rydberg 单位制下薛定谔方程简单，系数为1。Hartree 单位制下，一个长度单位等于 $1L_bohr = 0.5292 Å$ ，一个能量单位 $1E_{Hartree} = 27.21 eV$ ，约化普朗克常数 ℏ=1。这样有效质量表达式中的约化普朗克常数就没了。

根据原胞基矢和正倒格子基矢间对应关系，算出倒格子基矢

（1）在笛卡尔坐标下，三个正格子基矢的坐标为 $(\vec{a}_{1},\vec{a}_{2},\vec{a}_{3})$ (单位: $\AA$ )，转换为 Harree单位制下的 $(\vec{a}_{1}^{^{\prime}},\vec{a}_{2}^{^{\prime}},\vec{a}_{3}^{^{\prime}}),$ ，其中 $\vec{a}_{1}^{^{\prime}}=\vec{a}_{1}/0.5292,\vec{a}_{2}^{^{\prime}}=\vec{a}_{2}/0.5292,\vec{a}_{3}^{^{\prime}}=\vec{a}_{3}/0.5292,$
（2）
方法一：根据正格子基矢与倒格子基矢之间的关系，计算出倒格子基矢 $(\vec{b}_{1},\vec{b}_{2},\vec{b}_{3})$ ，
$\begin{aligned} & \vec{b}_{1} & & =\frac{2\pi}{V}(\vec{a}_{2}\times\vec{a}_{3}) \\ & \vec{b}_{2} & & =\frac{2\pi}{V}(\vec{a}_{3}\times\vec{a}_{1}), & V=({\vec{a}}_{1}\times{\vec{a}}_{2})\cdot{\vec{a}}_{3} \\ & \vec{b}_{3} & & =\frac{2\pi}{V}(\vec{a}_{1}\times\vec{a}_{2}) \end{aligned}$
方法二：采用由正格子基矢算倒格子基矢的python脚本进行转换。
$\begin{aligned} & \vec{b}_{1}=[x_{1},0,0] \\ & \vec{b}_{2}=[0,x_{2},0]\quad\Rightarrow\quad b= \begin{pmatrix} x_{1} & & 0 & & 0 \\ 0 & & x_{2} & & 0 \\ 0 & & 0 & & x_{3} \end{pmatrix} \\ & \vec{b}_{3}=[0,0,x_{3}] \end{aligned}$

(a)在 infile 中写入晶格常数

inunit ang 
_begin_vectors 
4.0836222599999994 -0.0000000010 0.0000000000000000 
0.0000000000 7.070341233294212 0.0000000000000000 
0.0000000000 0.0000000000 25.377516849029358 
_end_vectors

(b)运行程序:./crecip.py infile outfile
（c) 在outfile中找到reciprocal vectors in $\frac{1}{bohr}$ ，下面即为倒格子基矢，写成矩阵形式

reciprocal vectors in 1/bohr:
0.814208138  0.000000000  0.000000000
0.000000000  0.470083288  -0.000000000
-0.000000000  0.000000000  0.131018275

$\Rightarrow b = \begin{pmatrix} 0.814208138 & 0 & 0 \\ 0 & 0.470083288 & 0 \\ 0 & 0 & 0.131018275 \end{pmatrix}$

将VASP计算band时的k点坐标（分数坐标）转变为笛卡尔坐标

(1)k点分数坐标如下:
$\begin{aligned} & \mathrm{Y:}( \begin{array} {ccc}{0} & {0.5} & {0} \end{array}) \\ & \Gamma:(0\quad0\quad0) \\ & X:(0.5\quad0\quad0) \\ & \mathrm{S:}(0.5\quad0.5\quad0) \\ & \mathrm{Y:}( \begin{array} {ccc}{0} & {0.5} & {0} \end{array}) \end{aligned}$
(2) 转换为笛卡尔坐标：
$\begin{aligned} & \mathbf{Y}=(0\quad0.5\quad0) \begin{pmatrix} 0.814208138 & 0 & 0 \\ 0 & 0.470083288 & 0 \\ 0 & 0 & 0.131018275 \end{pmatrix}=(0\quad0.235041644\quad0) \\ & \Gamma=(0\quad0\quad0) \begin{pmatrix} 0.814208138 & 0 & 0 \\ 0 & 0.470083288 & 0 \\ 0 & 0 & 0.131018275 \end{pmatrix}=(0\quad0\quad0)\\ & \mathrm{X=}(0.5\quad0\quad0) \begin{pmatrix} 0.814208138 & 0 & 0 \\ 0 & 0.470083288 & 0 \\ 0 & 0 & 0.131018275 \end{pmatrix}=(0.407104069\quad0\quad0) \\ & S=(0.5\quad0.5\quad0) \begin{pmatrix} 0.814208138 & 0 & 0 \\ 0 & 0.470083288 & 0 \\ 0 & 0 & 0.131018275 \end{pmatrix}=(0.407104069\quad0.235041644\quad0) \\ & \mathrm{Y=}(0\quad0.5\quad0) \begin{pmatrix} 0.814208138 & 0 & 0 \\ 0 & 0.470083288 & 0 \\ 0 & 0 & 0.131018275 \end{pmatrix}=(0\quad0.235041644\quad0) \end{aligned}$

根据两点间的距离公式，计算出各K点之间的距离

$\begin{aligned} & \left|AB\right| ={\sqrt{\left(x_{1}-x_{2}\right)^{2}+\left(y_{1}-y_{2}\right)^{2}+\left(z_{1}-z_{2}\right)^{2}}} \\ & \mathrm{|Y\Gamma}|=0.235041644\\ & \left|\Gamma\mathrm{X}\right|=0.407104069 \\ & \left|\mathrm{XS}\right|=0.235041644 \\ & \left|\mathrm{SY}\right|=0.407104069 \end{aligned}$

求每个K点的位置值

根据VASP计算能带时各高对称点间均匀撒点，求出每个点的位置值，第一个点设为0，本例中为80个点，在excel中进行操作。因计算时均匀撒点80个，故有79个小间隔，对于 $∣ Y Γ∣$ 来说，每个小间隔为0.002975210683544，故1-80个点的坐标值都可算出，以此类推，后面的点的坐标在前面点的基础上加上间隔即可。（注意：在80个点结束处和81个点开始处的值是一样的，后面的点类似。）
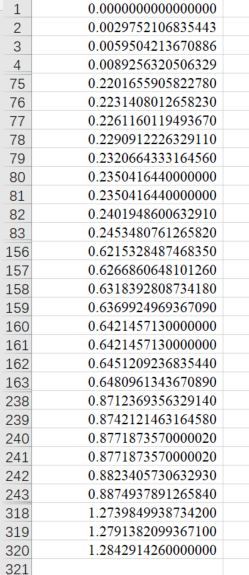
在这里插入图片描述

画出价带顶和导带底的能带

在origin中找出能带数据的价带顶（VBM）和导带底（CBM）的数据，把上面计算得到的K点路径做为X轴，VBM和CBM作为Y轴，在origin中画图如下：
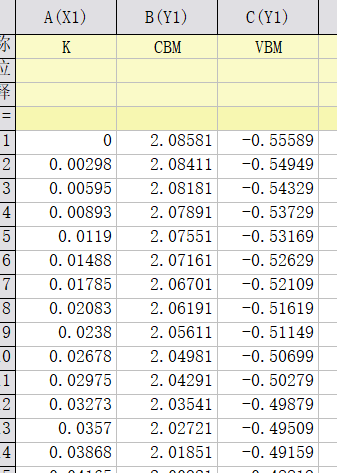
在这里插入图片描述

计算有效质量（以x方向电子的有效质量为例）

首先换算能量单位，由eV换算为原子单位制下的能量CBM/27.21然后选取
-X方向上以Γ开始的4-8个点的数据画能带图，如下:

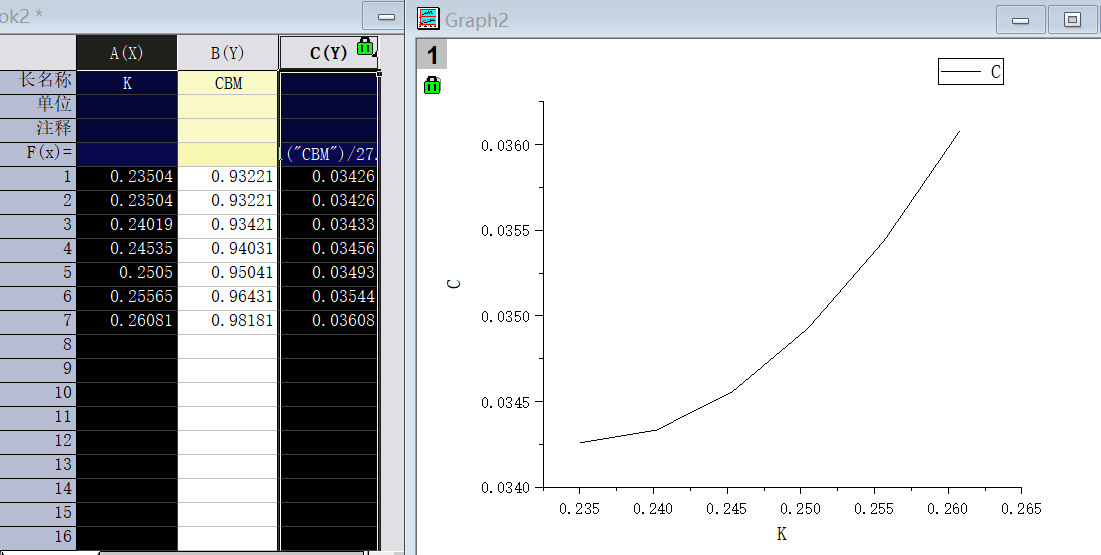
用 $y=a+bx+cx^2$ 函数拟合，操作如下:
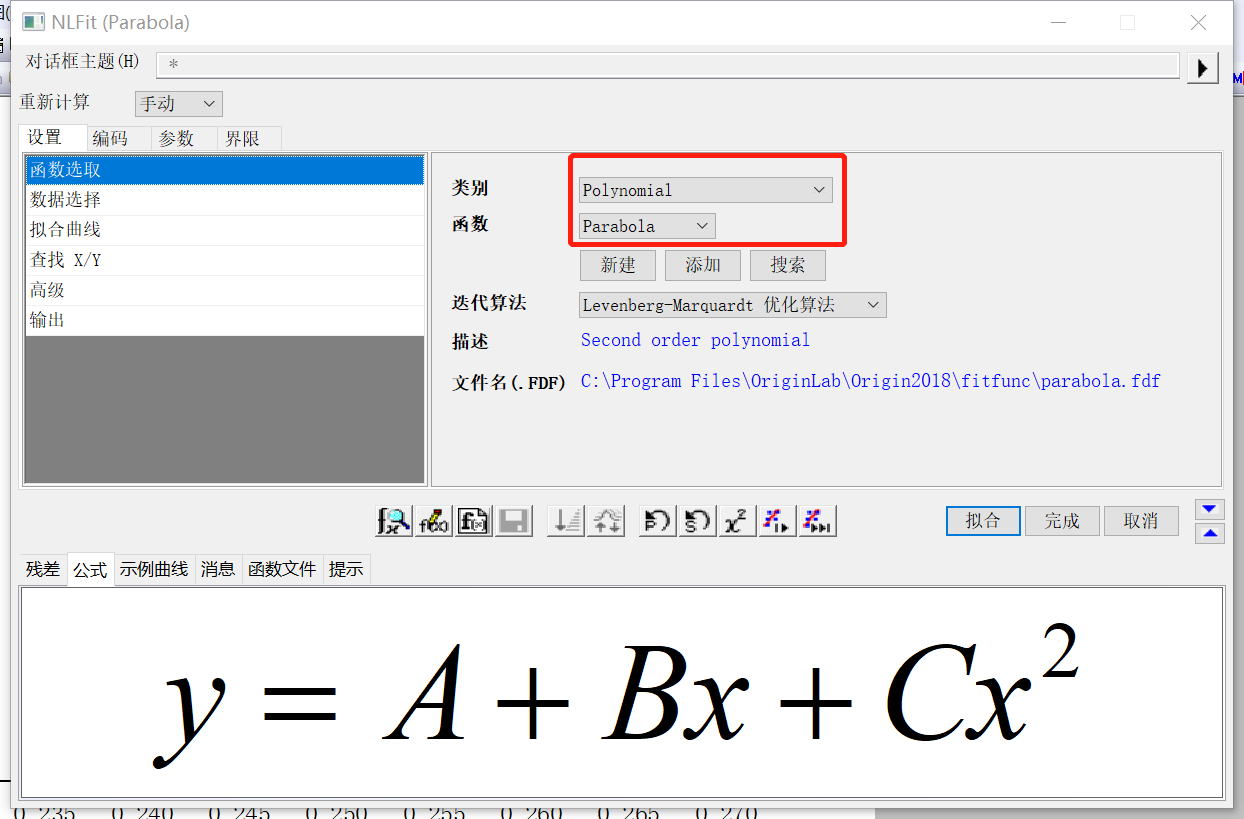
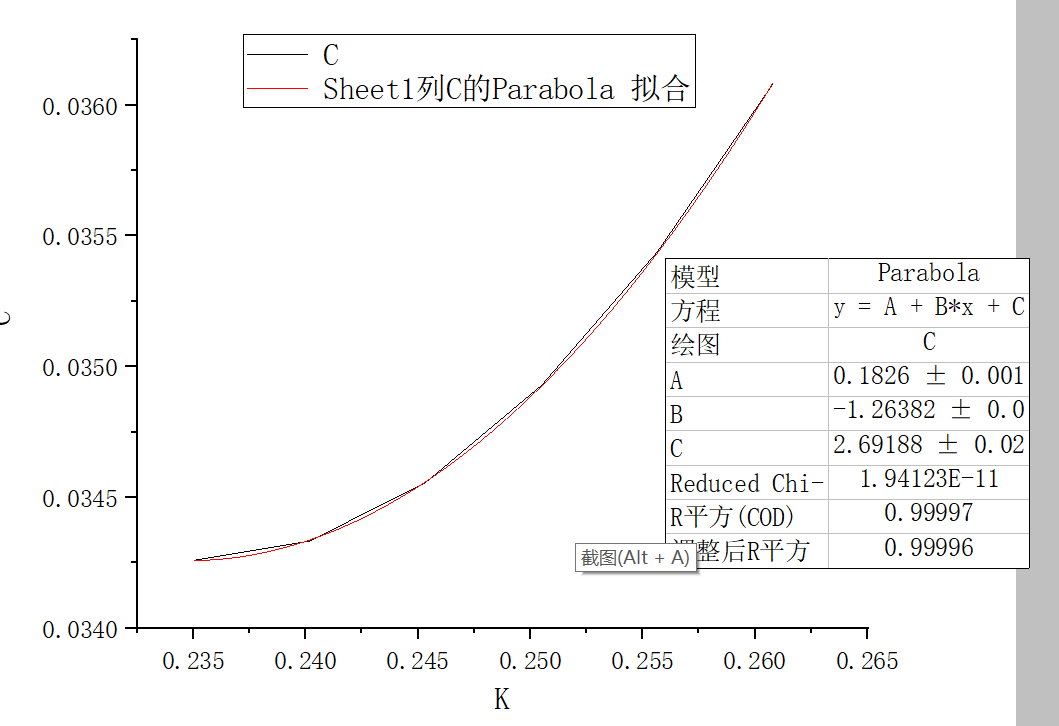
在这里插入图片描述

有效质量为 $\frac{1}{2c}$ ，其中 $C = 2.69188$ ，算得有效质量为0.19 ，为电子沿x方向的质量。文献计算结果为0.19，符合一致。

二维InSe载流子迁移率计算过程

本文载流子迁移率的计算依据的是形变势理论，因此需要对二维InSe的x方向和y方向施加应变，施加应变的范围是-2%~2%。为了计算的准确性，计算过程中考虑了泊松效应，即对x轴施加应变时，固定x轴和z轴，优化y方向的晶格常数；对y轴施加应变时，固定y轴和z轴，优化x方向的晶格常数。

能带计算过程

准备输入文件

首先建立mobility文件夹，然后在该文件夹下建立初始文件夹，命名为IS-x和IS-y，其结构目录如下：

$ tree mobility
mobility
├── IS-x
│   ├── 2_scf
│   │   ├── band
│   │   │   ├── INCAR
│   │   │   ├── KPOINTS
│   │   │   └── POTCAR
│   │   ├── INCAR
│   │   ├── KPOINTS
│   │   └── POTCAR
│   ├── INCAR
│   ├── KPOINTS
│   ├── OPTCELL
│   ├── pbs
│   ├── POSCAR
│   └── POTCAR
├── IS-y
│   ├── 2_scf
│   │   ├── band
│   │   │   ├── INCAR
│   │   │   ├── KPOINTS
│   │   │   └── POTCAR
│   │   ├── INCAR
│   │   ├── KPOINTS
│   │   └── POTCAR
│   ├── INCAR
│   ├── KPOINTS
│   ├── OPTCELL
│   ├── pbs
│   ├── POSCAR
│   └── POTCAR
└── mobility.sh

说明：

pbs文件：

#!/bin/bash
#PBS -N mobility
#PBS -l nodes=1:ppn=16
#PBS -m abe
#PBS -j n
##PBS -o job.log
##PBS -e job.err
#PBS -l walltime=120:00:00
cd $PBS_O_WORKDIR
date "+01 Today's date is: %D. The time execution %T" >> time.info
mpirun -np 16 /your-path/vasp.5.4.4/build/std/vasp  > log
date "+02 Today's date is: %D. The time finish %T" >> time.info
cp ./CONTCAR ./2_scf/POSCAR
cd ./2_scf/
date "+01 Today's date is: %D. The time execution %T" >> time.info
mpirun /your-path/vasp.5.4.4/build/std/vasp  > log
date "+02 Today's date is: %D. The time finish %T" >> time.info
cp ./CONTCAR ./band/POSCAR
cp ./WAVECAR ./band/
cd ./band/
date "+01 Today's date is: %D. The time execution %T" >> time.info
mpirun -np 16 /your-path/vasp.5.4.4/build/std/vasp  > log
date "+02 Today's date is: %D. The time finish %T" >> time.info

OPTCELL文件 —X 方向—

000
010
000

自洽计算时INCAR文件中加入计算真空能级的命令

LVHAR = .TRUE.

mobility.sh文件

#!/bin/bash
#3 November, 2018
#To use it: bash mobility.sh
mkdir mobility-x
cd mobility-x
x=4.083622259999999                           #"x" stands for the lattice constant in x direction
for i in $(seq 0.98 0.005 1.02)                #"i" defines the range of strain
do
cp -r ../IS-x ./$i                               #"IS-x" stands for the origin file 
sed -i "3s/$x/$(echo "$x*$i"|bc)/g" $i/POSCAR
cd $i
qsub ./pbs
cd $OLDPWD
done
cd ../
mkdir mobility-y
cd mobility-y
y=7.073041233239241                            #"y" stands for the lattice constant in y direction
for j in $(seq 0.98 0.005 1.02)                #"j" defines the range of strain
do
cp -r ../IS-y ./$j                               #"IS-y" stands for the origin file 
sed -i "4s/$y/$(echo "$y*$j"|bc)/g" $j/POSCAR
cd $j
qsub ./pbs
cd $OLDPWD
done

Note：计算过程中需要根据自己的体系修改x和y方向的晶格常数值

其余文件与前面计算能带过程的输入文件相同，在mobility文件夹下输入bash mobility.sh文件即可完成全部计算。

数据处理（以x方向为例）

计算形变势常数

以真空能级为参考，确定VBM和CBM的位置。思路是读取能带计算结果中的最高占据态VBM和最低非占据态CBM（未扣除费米能级）的结果，然后减去真空能级就可得到我们需要的结果。
对得到的数据以应变量为x轴（-0.02~0.02），VBM和CBM为y轴画图，然后在origin中做线性拟合，即可得到形变势常数，最终结果如下：

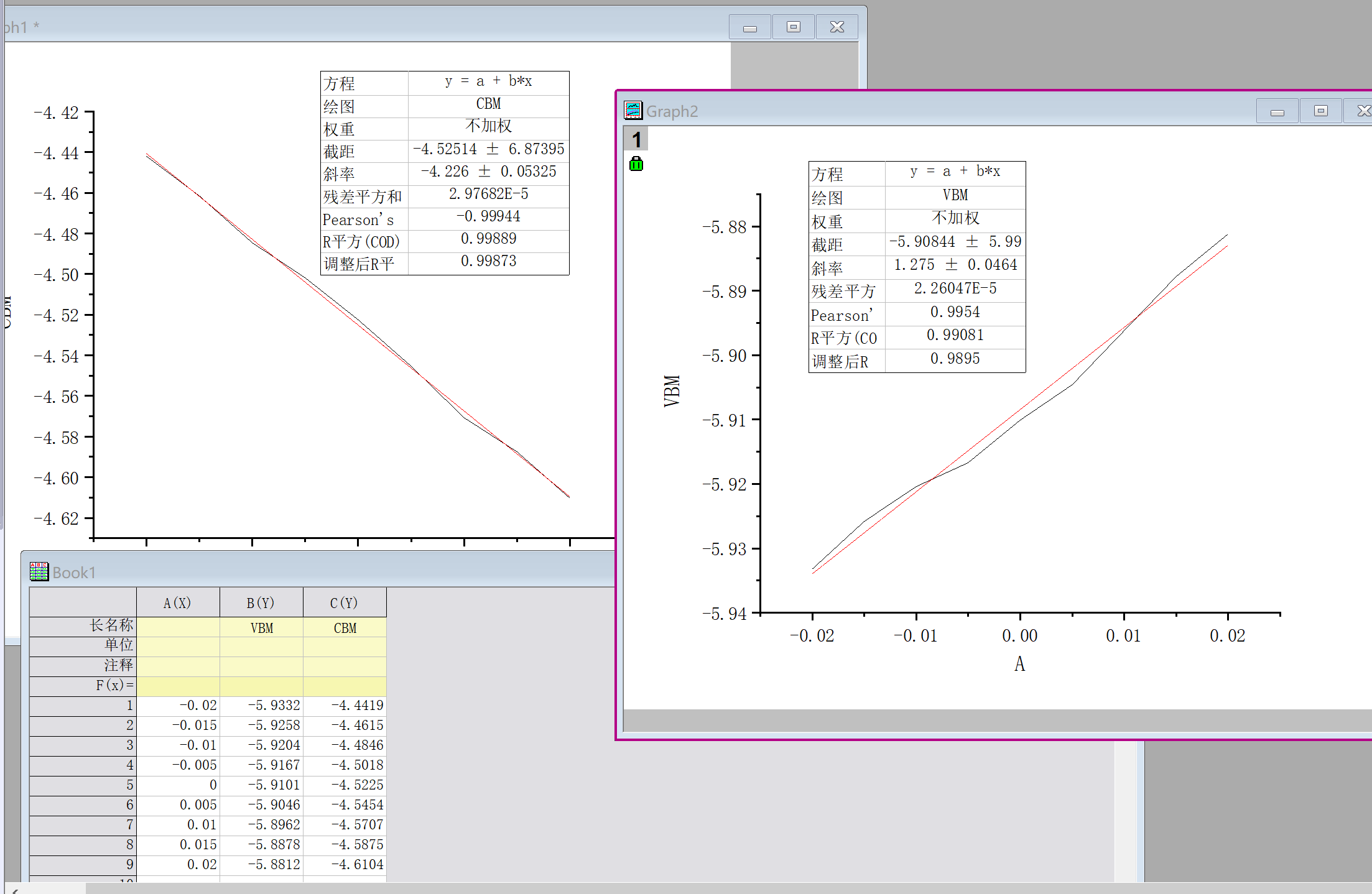
计算弹性模量（以x方向为例）

读取每个应变下的体系总能量，然后画图。
对其做二次函数拟合，然后带入的计算公式，并对单位做换算后，得到的结果如下：

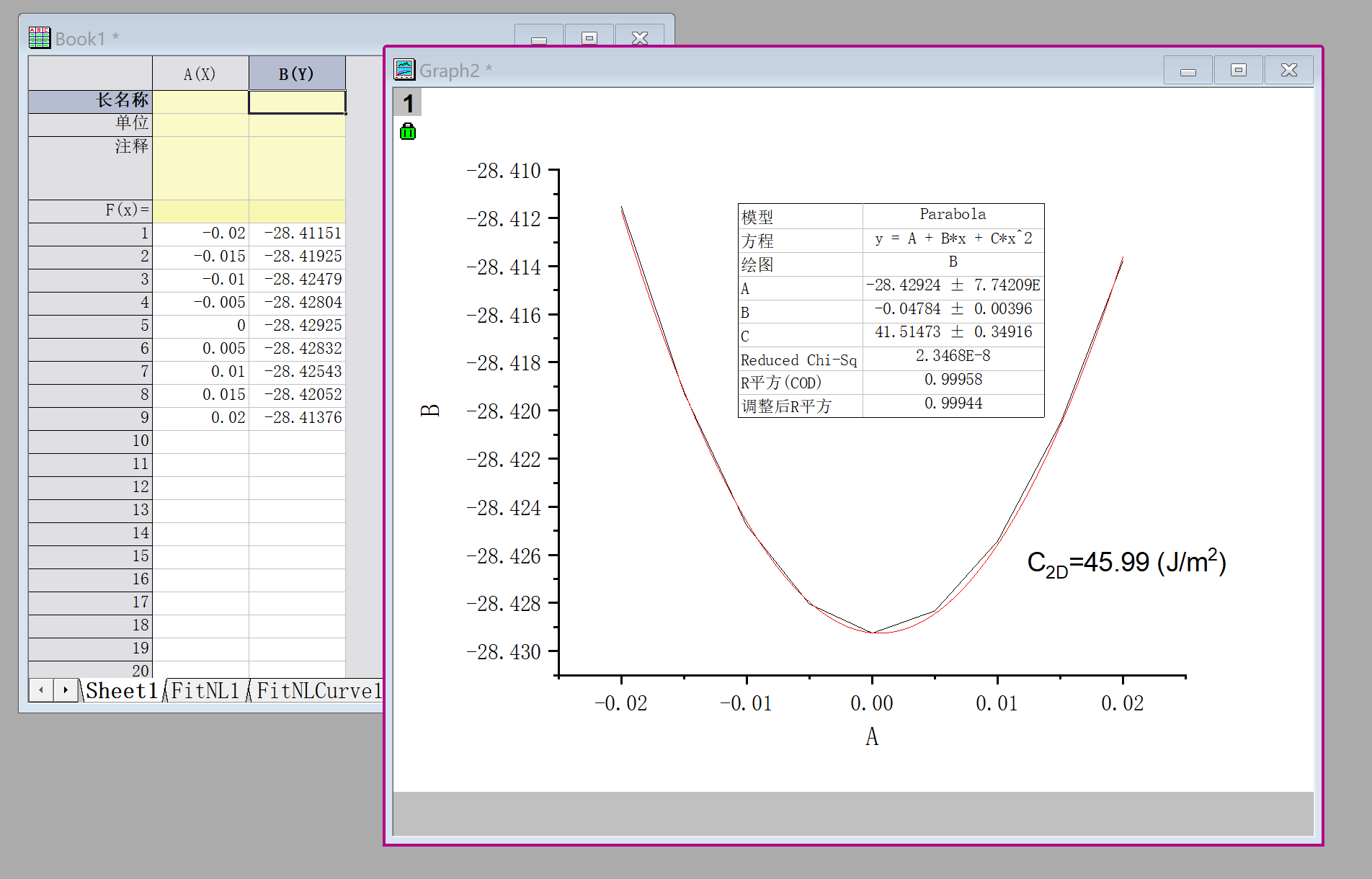
计算迁移率

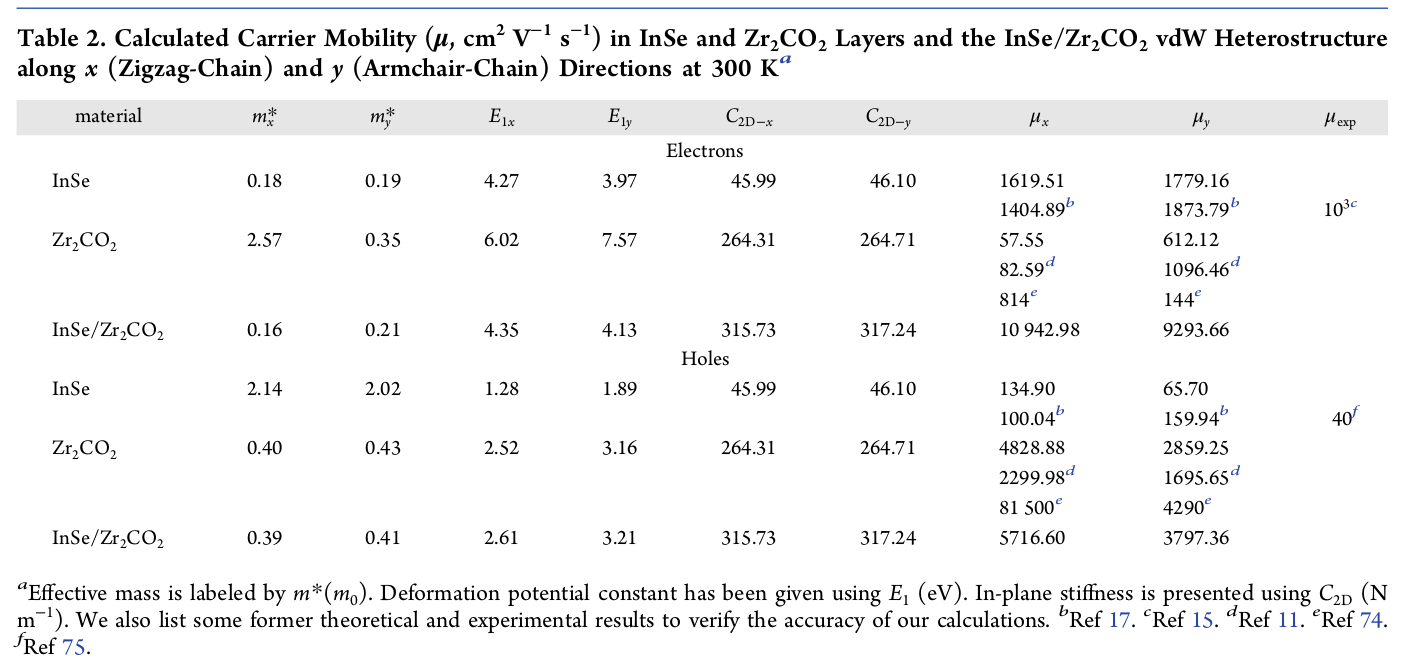
现已得到有效质量、形变势常数和弹性模量，依据载流子迁移率计算公式，并注意单位换算，即可得到载流子的迁移率具体数值。计算结果可参考我的JPCC文章，如下：
在这里插入图片描述

后记

因时间关系，本文写作比较仓促，文中一些数据处理的细节没有详细给出，并且可能存在一些小的错误，欢迎大家阅读过程中积极指出，以便在后续更正过程中改正。另外，本文公式较多，但mathjax环境对公式编辑不是很友好，排版过程中公式很容易乱，故而部分公式以插图的形式放入了本文中，看起来版面搅乱，后续会想办法处理。