参考书籍:《统计学习方法.李航》
感知器模型
f(x) = sign( w*x + b )
其中x为实例的特征向量(输入),y表示实例的类别(输出),w叫作权值,b叫作偏置,sign为符号函数。
几何解释:w*x+b=0对应特征空间中的一个超平面S,其中w为法向量,b为斜距,这个超平面将特征空间划分为正、负两类。感知器学习就是由训练数据集求得感知器模型的模型参数w和b;感知器预测就是通过学习得到的感知器模型,对于新的输入实例给出其对应的输出类别。
数据集的线性可分性:给定一个数据集,如果存在某个超平面S(w*x+b=0)能够将数据集的正实例点和负实例点正确划分到超平面的两侧,则称数据集是线性可分数据集,否则为线性不可分。(如在二维空间中可以用一条直线将两类分开,三维空间中可以用一个平面将两个类别分开)
感知器学习策略
即定义一个损失函数并将损失函数极小化。
损失函数:误分类点到超平面的总距离。
任意一点x0到超平面S的距离:
根据推导得到损失函数为:
(忏悔Ing…我应当学下如何在csdn博客中插入漂亮的公式)感知器学习算法
即求解损失函数式的最优化问题,方法选择的是随机梯度下降法。这意味着极小化过程中不是一次使M中所有误分类点的梯度下降,而是一次随机选取一个误分类点使其梯度下降。
训练过程:
(1)选取初值w0,b0;
(2)在训练集中选取数据(xi,yi);
(3)如果错误分类,即yi(w*xi+b)<0,则:w<-w+nyixi, b<-b+nyi,其中n(0~1)为学习率。感知器学习算法在采用不同的初值或者选取不同的误分类点时,得到的解可以不同。
感知器算法的收敛性
当训练集线性可分时, 经过证明,误分类的次数K是有上界的,经过有限次搜索可以找到将训练数据完全正确分开的分离超平面。当训练集线性不可分时,感知器学习算法不收敛,迭代结果会发生震荡。
针对多解情况:对分离超平面增加约束条件(如线性支持向量机)感知器python实现
做了一下书上给的例题:
# -*- coding: utf8 -*-
w = []#权向量
b = 0 #偏置
n = 1 #学习率
lens = 0 #训练集合中数据长度
def judge(data):
global w,b,n,lens
ans = 0
for index in range(lens-1):
ans += w[index]*data[index]
ans += b
ans *= data[l







 本文介绍了感知器模型的数学表达式和几何解释,强调了线性可分数据集的概念,并详细阐述了感知器的学习策略、损失函数及随机梯度下降法在训练过程中的应用。此外,还探讨了感知器算法的收敛性和在线性不可分数据集上的行为。最后,通过一个书中的例题展示了感知器的Python实现。
本文介绍了感知器模型的数学表达式和几何解释,强调了线性可分数据集的概念,并详细阐述了感知器的学习策略、损失函数及随机梯度下降法在训练过程中的应用。此外,还探讨了感知器算法的收敛性和在线性不可分数据集上的行为。最后,通过一个书中的例题展示了感知器的Python实现。
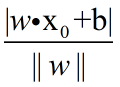
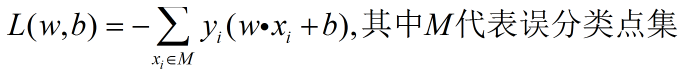
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 576
576

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








