反素数深度分析 (转)

最新推荐文章于 2022-03-02 21:44:21 发布

小鸡炖蘑菇_

最新推荐文章于 2022-03-02 21:44:21 发布

阅读量439

点赞数

分类专栏：数论 algorithm

数论同时被 2 个专栏收录

60 篇文章 0 订阅

订阅专栏

algorithm

57 篇文章 3 订阅

订阅专栏

今天要我要讲的是反素数，在ACM中也算是常见的考点，那么对于搞ACM的同学来说，很有必要搞清楚它，所以接下来我会很详细地讲解。
在讲解反素数之前，我们先来看反素数的概念。
反素数的定义：对于任何正整数n，其约数个数记为f(n)，例如f(6)=4，如果某个正整数n满足：对任意的正整数i(0<1<n)，都有f(i)<f(n)，那么称为n反素数。
从反素数的定义中可以看出两个性质：
（1）一个反素数的所有质因子必然是从2开始的连续若干个质数，因为反素数是保证约数个数为的这个数尽量小
（2）同样的道理，如果n=2^t₁*3^t₂*5^t₃…，那么必有t₁≥t₂≥t₃≥….

在ACM竞赛中，最常见的问题如下：
（1）给定一个数n，求一个最小的正整数x，使得x的约数个数为n
（2）求出中1~n约数个数最多的这个数
从上面的性质中可以看出，我们要求最小的x，它的约数个数为n，那么可以利用搜索来解。
以前我们求一个数的所有因子也是用搜索，比如n=p₁^a₁p₂^a₂p₃^a₃，以每一个为树的一层建立搜索树，深度为k
以12=2²*3为例进行说明，建树如下：
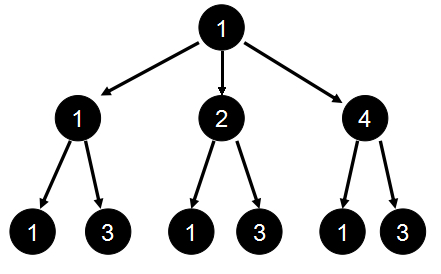
这里写图片描述
可以看出从根节点到每一个叶子结点这条路径上的所有数字乘起来都是12的约数，所以12有6个约数。
搜索的思路就明显了，从根节点开始进行深搜，到叶子结点，代码如下：

void dfs(int dept,LL ans = 1)
{
    if(dept == cnt)
    {
        fac[ct++] = ans;
        return;
    }
    for(int i=0;i<=num[dept];i++)
    {
        dfs(dept+1,ans);
        ans *= pri[dept];
    }
}

回到我们的问题，同样用搜索来求最小的x。
题目：http://codeforces.com/problemset/problem/27/E

题意：给一个数n，求一个最小的正整数，使得它的因子个数为n。

分析：与求因子的方法类似，先建立搜索树，以每一个p_i为一层建立树型结构，进行搜索，取最小的。

#include <iostream>
#include <cstdio>
#define N 1005
#define ull unsigned long long
using namespace std;
const ull INF = -1ull;
int p[]={2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53};
int n;
ull ans;
void dfs(int depth, ull tmp, int num)
{
    if (num > n)    return ;
    if (num == n && ans > tmp)  ans = tmp;
    for (int i = 1; i <= 63; i++)
    {
        if (ans/p[depth] < tmp) break;
        dfs(depth+1, tmp*=p[depth], num*(i+1));
    }
}
int main() 
{
#ifndef ONLINE_JUDGE
//  freopen("1.txt", "r", stdin);
#endif
    cin >> n;
    ans = INF;
    dfs(0, 1, 1);
    cout << ans;
    return 0;
}

题目：http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemId=1562

题意：求n以内的因子最多的那个数。

分析：基本上跟上题差不多。

#include <iostream>
#include <iomanip>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <string>
#include <cmath>
#include <algorithm>
#define N 1005
#define ull unsigned long long
using namespace std;
const ull INF = -1ull;
int p[]={2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53};
int  best;  //best表示ans的约数的个数
ull n, ans; //ans表示约数最多的数,ans和n都需要时unsigned long long 类型的，不然会WA
void dfs(int depth, ull tmp, int num)
{
    if (depth >= 16)    return ;//到叶子节点，返回
    if (num > best) //更新best和ans 
    {
        best = num;
        ans = tmp;
    }
    if (best == num && ans > tmp)   ans = tmp;
    for (int i = 1; i <= 63; i++)
    {
        if (n/p[depth] < tmp)   break;
        dfs(depth+1, tmp*=p[depth], num*(i+1));
    }
}
int main() 
{
#ifndef ONLINE_JUDGE
//  freopen("1.txt", "r", stdin);
#endif
    while(cin >> n)
    {
        ans = INF;
        best = 0;
        dfs(0, 1, 1);
        cout << ans << endl;
    }
    return 0;
}

题目：http://acm.timus.ru/problem.aspx?space=1&num=1748

分析：这道题主要注意数据处理。对于上面的两题，数据范围小，所以可以不用剪枝，本题就需要了。

#include <iostream>
#include <iomanip>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <string>
#include <cmath>
#include <algorithm>
#define N 1005
#define ull unsigned long long
using namespace std;
const ull INF = -1ull;
int p[]={2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53};
int  best;  //best±íÊ¾ansµÄÔ¼ÊýµÄ¸öÊý
ull n, ans; //ans±íÊ¾Ô¼Êý×î¶àµÄÊý 
void dfs(int depth, int limit, ull tmp, int num)
{
    if (depth >= 16)    return ;
    if (num > best) //¸üÐÂbestºÍans 
    {
        best = num;
        ans = tmp;
    }
    if (best == num && ans > tmp)   ans = tmp;
    for (int i = 1; i <= limit; i++)
    {
        if (n/p[depth] < tmp)   break;
        dfs(depth+1, i, tmp*=p[depth], num*(i+1));
    }
}
int main() 
{
#ifndef ONLINE_JUDGE
//  freopen("1.txt", "r", stdin);
#endif
    int T;
    cin >> T;
    while(T--)
    {
        cin >> n;
        ans = INF;
        best = 0;
        dfs(0, 60, 1, 1);
        cout << ans << " " << best << endl;
    }
    return 0;
}

题目：http://acm.hdu.edu.cn/showproblem.php?pid=4542

题意：给出一个数K和两个操作
如果操作是0，就求出一个最小的正整数X，满足X的约数个数为K。
如果操作是1，就求出一个最小的X，满足X的约数个数为X-K。

分析：对于操作0，就是求反素数，直接搜索搞定。对于操作1，代表1至X中不是X的约数个数为K。

代码：

#include <iostream>
#include <iomanip>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <string>
#include <cmath>
#include <algorithm>
#define N 50005
#define ll long long
using namespace std;
const ll INF = ((ll)1<<62)+1;
int p[]={2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53};
ll ans;
int n, d[N], k;
void init()
{
    for (int i = 1; i < N; i++) d[i] = i;
    for (int i = 1; i < N; i++)
    {
        for (int j = i; j < N; j+=i)    d[j]--;
        if (!d[d[i]])   d[d[i]] = i;
        d[i] = 0;
    }
}
void dfs(int depth, int limit, ll tmp, int num)
{
    if (num > k || depth >= 16) return ;
    if (num == k && ans > tmp)      ans = tmp;
    for (int i = 1; i <= limit; i++)
    {
        if (ans/p[depth] < tmp || num*(i+1) > k)    break;
        tmp *= p[depth];
        if (k%(num*(i+1))==0)
            dfs(depth+1, i, tmp, num*(i+1));
    }
}

int main() 
{
#ifndef ONLINE_JUDGE
    freopen("1.txt", "r", stdin);
#endif
    int T, i, type;
    scanf("%d", &T);
    init();
    for (i = 1; i <= T; i++)
    {
        scanf("%d%d", &type, &k);
        if (type)   ans = d[k];
        else
        {
            ans = INF;
            dfs(0, 62, 1, 1);
        }
        printf("Case %d: ", i);
        if (ans == 0)   printf("Illegal\n");
        else if (ans >= INF) printf("INF\n");
        else    printf("%I64d\n", ans);
    }
    return 0;
}