CCF 201312-3 最大的矩形

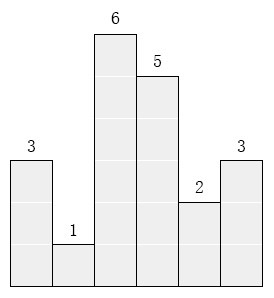
在横轴上放了n个相邻的矩形，每个矩形的宽度是1，而第i（1 ≤ i ≤ n）个矩形的高度是hi。这n个矩形构成了一个直方图。例如，下图中六个矩形的高度就分别是3, 1, 6, 5, 2, 3。

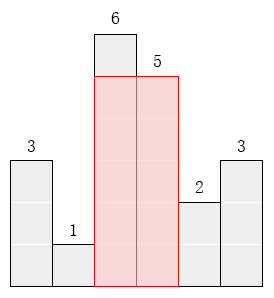
请找出能放在给定直方图里面积最大的矩形，它的边要与坐标轴平行。对于上面给出的例子，最大矩形如下图所示的阴影部分，面积是10。

输入格式
　　第一行包含一个整数n，即矩形的数量(1 ≤ n ≤ 1000)。
　　第二行包含n 个整数h1, h2, … , hn，相邻的数之间由空格分隔。(1 ≤ hi ≤ 10000)。hi是第i个矩形的高度。
输出格式
　　输出一行，包含一个整数，即给定直方图内的最大矩形的面积。
样例输入
6
3 1 6 5 2 3
样例输出
10

---

以上面图中给出的数据为例，最大的矩形是，2*5的大小，这个结果可以一眼就从图中扫出来。当遇到程序时，这要找到一个合理的判断过程，一步步来求解出最大的矩形面积。

从左至右开始看：

首先是数字3，以3为高度的矩形，长度最大为1，其矩形的面积为3*1=3。
其次是数字1，以1为高度的矩形，长度最大为6，则矩形面积为1*6=6。
再次是数字6，以6为高度的矩形，长度最大是1，则矩形面积为6*1=6。
接着是数字5，以5为高度的矩形，长度最大是2，则矩形面积为5*2=10。
。。。。。。
观察这个过程，如果要在O(n)的时间内找到最大的面积，则需要记录下来每个高度为N的矩形，其长度最大可以达到多少。这样就分为两种情况，如图中描述的，首先是高度N越来越大，其次是高度N越来越小。

1.在高度N越来越大时，其上一个数字构成的高度的矩形的最大长度则增加1，例如，2 3，高度为3时，则高度为2的矩形的长度就加1.

2.在高度N越来越小时，其上一个数字构成的高度的矩形的最大长度就不变，例如 4 3，高度为4时，其构成的矩形长度为1，到了3，矩形长度没有递增，而4之前的数字3构成的矩形的长度也加1。

有了上面这两条分析，就可以使用一个stack来存储矩形的高度和长度，其中长度会动态的变化。当遇到一个数字大于栈顶数字的时候就压入栈，小于栈顶的数字就弹出栈，在这个动态过程中，更新最大的矩形面积。

#include <iostream>
#include <iomanip>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <string>
#include <cmath>
#include <stack>
#include <algorithm>
#define ll long long
#define N 1010
using namespace std;
int a[1003];
int maxRect(int n) {
    int top = 0, Max = 0;
    int i = 0, pre, time;
    stack<pair<int,int> > sta;
    while(i < n) {
        if (a[i] > top) {
            sta.push(pair<int, int>(a[i], 1));
        } else {
            pre = 0;
            while(a[i] < top) {
                time = sta.top().second;
                pre += time;
                Max = max(Max, top*pre);
                sta.pop();
                if (!sta.empty()) {
                    top = sta.top().first;
                } else {
                    break;
                }
            }
            if (!sta.empty() && sta.top().first == a[i]) {
                sta.top().second += pre+1;
            } else {
                sta.push(pair<int,int>(a[i], pre+1));
            }
        }
        top = sta.top().first;
        i++;
    }
    pre = 0;
    while(!sta.empty()) {
        time = sta.top().second;
        top = sta.top().first;
        pre += time;
        Max = max(Max, top*pre);
        sta.pop();
    }
    return Max;
}
int main()
{
    int i, j, n;
    while(cin >> n) {
        int ans = 0;
        for (i = 0; i < n; i++) {
            cin >> a[i];
        }
        cout << maxRect(n) << endl;
    }
    return 0;
}