COT-为什么有时候不好使-Is Chain-of-Thought Reasoning of LLMs a Mirage? A Data Distribution Lens

论文：https://arxiv.org/pdf/2508.01191

该文档围绕“大语言模型（LLM）的思维链推理（CoT）是否为‘幻象’”展开研究，核心内容可概括为以下几点：

一、研究核心视角与假设

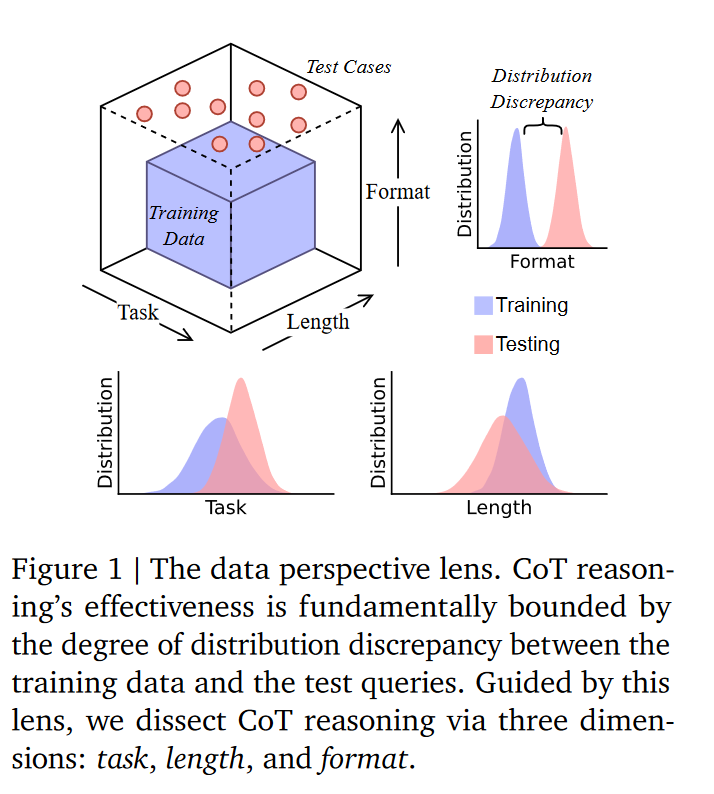
从“数据分布”角度切入，提出核心假设：CoT推理并非真正的逻辑推理，而是模型对训练数据中结构化模式的匹配——其效果受限于训练数据与测试查询的分布差异，一旦测试场景偏离训练分布，性能会显著下降。

二、关键实验设计：DataAlchemy环境

为验证假设，构建了可控的实验框架DataAlchemy，可从零训练LLM，并从三个维度系统测试CoT的泛化能力：

• 任务泛化：测试模型对新任务结构（如 novel 元素、变换组合）的适应能力；

• 长度泛化：考察输入文本长度、推理步骤数与训练数据不同时的性能；

• 格式泛化：通过插入噪声、删除/修改token等扰动，测试CoT对查询格式变化的敏感度。

三、核心实验结论

• CoT依赖训练分布：仅在与训练数据分布一致或接近时有效，轻微偏离（如新变换、长度变化）就会导致性能骤降，暴露其“表面推理”本质；

• 各维度脆弱性：任务维度中，新元素/变换组合会让准确率趋近于0；长度维度中，偏离训练长度（如训练4个原子，测试3/5个）时推理失效；格式维度中，插入噪声对性能影响最大，且查询中的“元素”“变换”是关键，改其他token影响小；

• 温度与模型规模影响小：在合理温度范围（1e-5~1）内，CoT稳定性不受温度影响；不同规模模型（从68K参到543M参）性能差异小，无需依赖超大模型；

• 微调非“万能药”：微调（SFT）可小幅扩大模型“分布范围”，但无法解决“缺乏抽象推理能力”的核心问题，仅为临时补丁。

四、实践与研究启示

• 对从业者：勿将CoT视为“即插即用”工具，高风险领域（医疗、金融）需专家审核；需加强“分布外（OOD）测试”，而非仅用相似训练数据验证；

• 对研究者：当前CoT的脆弱性表明LLM缺乏真正推理能力，未来需研发突破“模式匹配”、具备抽象推理能力的模型。

五、研究价值

打破了“CoT体现LLM类人推理能力”的认知，从数据分布视角揭示其本质，为LLM推理能力的评估与优化提供了明确方向，同时通过DataAlchemy框架为后续相关研究提供了可控实验范式。

1 大型语言模型（LLMs）的 “思维链（CoT）推理” 能力

一、核心内容速览

通过数据分布视角揭示其本质：CoT 推理并非真正的逻辑推理，而是模型对训练数据中模式的复用，在数据分布偏移时极易失效，并通过自主设计的实验框架验证了这一观点，为学界和业界提供了新认知。

二、关键信息拆解与解读

研究背景：CoT 推理的 “表面成功”

• 基础概念：CoT 推理是通过 “逐步思考” 等提示，让 LLMs 将复杂问题拆分为中间步骤的推理方法，比如让模型一步步解数学题、分析逻辑关系。

• 表面效果：此前研究显示，它在逻辑推理、数学求解、常识判断等任务中表现出色，例如能清晰列出 “闰年判断规则” 再得出结论，这让人们误以为 LLMs 具备了和人类一样的审慎推理能力。

核心矛盾：看似合理的 “推理幻象”

• 典型案例：面对 “美国建国年份是闰年还是平年” 的问题，Gemini 模型先正确梳理：“1776 年能被 4 整除、非整百年→是闰年”，却最终结论为 “平年”。

• 矛盾本质：模型能复述规则、摆出推理步骤（表层逻辑），但无法完成逻辑闭环（底层推理）。这说明CoT 推理只是 “模仿人类推理的形式”，而非 “遵循人类推理的逻辑”。

• 学界佐证：已有研究发现，LLMs 推理依赖表层语义（如关键词、句子结构）而非逻辑 —— 比如加入无关信息就会出错，复杂任务中推理路径混乱，进一步质疑了 CoT 推理的真实性。

研究设计：从数据分布视角 “拆穿幻象”

• 核心假设：CoT 推理的效果来自模型从 “分布内数据”（训练时见过的同类数据）中学会的 “结构化归纳偏置”，简单说就是 “记住了类似问题的推理模板”，而非掌握了逻辑规则。

• 三维拆解：从三个维度测试 CoT 推理的局限性：

  • 任务维度：能否处理没见过的任务结构（如全新的逻辑转换题）；

  • 长度维度：能否适应比训练时更长 / 更短的推理链（如从 3 步推理到 10 步推理）；

  • 格式维度：是否受问题表述变化影响（如换种问法就出错）。

• 实验工具：设计 “DataAlchemy” 框架，从零训练 LLMs，排除预训练中复杂模式的干扰，精准测试 “数据分布偏移” 的影响。

关键发现：分布偏移下的 “脆弱性暴露”

• 当测试数据和训练数据相似（分布内）时，CoT 推理表现正常；

• 一旦数据出现中度偏移（如任务结构、推理长度变化），模型立刻失效，甚至生成 “流畅但逻辑矛盾” 的内容；

• 结论：所谓的 “结构化推理” 是幻象，本质是对训练数据中模式的记忆或拼接，而非逻辑推导。

研究价值：对实践与研究的双重启示

• 对实践者（如企业、开发者）：警惕将 CoT 当作 “万能推理工具”，不能把模型的 “步骤化输出” 等同于 “正确推理”，比如用 CoT 处理金融分析、医疗诊断等关键任务时需格外谨慎。

• 对研究者：明确了当前 LLMs 推理的短板 —— 缺乏 “忠实且可泛化的逻辑能力”，未来需突破 “表层模式识别”，开发真正能理解底层逻辑的模型。

• 核心贡献：提供了 “数据分布” 这一新视角解释 CoT 推理的成败，用可控实验验证了结论，重构了对 LLMs 推理能力的认知。

2 思维链（Chain-of-Thought, CoT）提示法的兴起

思维链（Chain-of-Thought, CoT）提示法的兴起，为解锁大型语言模型（Large Language Models, LLMs）的推理能力提供了关键路径。然而，随着研究的深入，其技术本质与能力边界逐渐引发学界争议。

2.1 LLM 提示工程与 CoT 推理的技术演进

CoT 推理的核心创新在于通过自然语言提示引导模型将复杂问题分解为序列化的中间推理步骤，打破了传统提示法 “直接输出答案” 的局限，被视为激发 LLM 推理能力的革命性突破（Wei et al., 2022）。在少样本学习场景中，通过在示例中附加完整推理链，CoT 在数学问题求解（Imani et al., 2023）、逻辑推理（Xu et al., 2024）等任务中实现了显著性能提升，使模型输出呈现出类人推理的结构化特征。

为适配不同应用场景，CoT 技术衍生出多类变体，形成了覆盖 “效率 - 精度 - 灵活性” 的技术体系：

• 轻量化变体：零样本 CoT 通过 “让我们逐步思考” 等指令性提示，无需示例即可触发推理过程（Kojima et al., 2022），大幅降低了技术使用门槛；Auto-CoT 则利用模型自身生成高质量推理示例，有效减少人工标注成本（Zhang et al., 2023）。

• 精度优化变体：自一致性方法通过生成多个独立推理链并采用多数投票策略聚合结果，显著降低了单一推理路径的随机性误差（Wang et al., 2023）。

• 结构升级变体：思维树（Tree-of-Thought, ToT）将线性推理链扩展为树状搜索空间，支持对中间步骤的前瞻评估与回溯调整（Yao et al., 2023）；长篇幅 CoT 则通过生成长文本推理过程，实现了错误修正、多路径探索等复杂操作（Guo et al., 2025）。

这些技术突破使学界普遍认为 LLMs 已具备 “涌现性类人推理能力”，但这一认知尚未经受过对 “推理本质” 的深度拷问 ——CoT 所呈现的结构化输出，究竟源于逻辑推理能力还是模式匹配机制，成为亟待澄清的核心问题。

2.2 CoT 推理的本质争议：“推理幻象” 的实证揭露

近年来，越来越多的实证研究对 CoT 推理的真实性提出质疑，揭示其看似合理的推理过程实则可能是 “模拟推理的文本幻象”，主要表现为三大核心缺陷：

2.2.1 推理过程的脆弱性

CoT 推理高度依赖表层语义线索而非底层逻辑结构。研究表明，在问题中加入 “干扰性短语”“符号形式变更” 等语义无关的扰动后，即使是最先进的 LLM 也会出现显著性能下降（Mirzadeh et al., 2024；Tang et al., 2023）。例如在闰年判断任务中，若问题附加 “小明今天穿了红色外套” 等无关信息，模型可能因对冗余线索的过度敏感而偏离核心逻辑，暴露其无法有效筛选关键推理信息的短板。

2.2.2 形式优先于逻辑的倾向

模型对推理过程的 “表面合理性” 的关注度远超 “逻辑正确性”。Bentham 等人（2024）的实验显示，在部分任务中，包含明显逻辑漏洞的长篇推理路径（如 “1776 能被 4 整除→是整百年→故为闰年”）反而能比简洁正确的推理路径（如 “1776 非整百年且能被 4 整除→闰年”）产生更符合预期的答案。这表明模型本质上是在 “模仿推理文本的格式”，而非 “执行逻辑推导的过程”。

2.2.3 推理与结论的非忠实性

“透明幻象”（illusion of transparency）现象进一步印证了 CoT 推理的虚假性：当研究者篡改或省略模型生成的中间推理步骤后，最终答案往往保持不变（Lanham et al., 2023；Chen et al., 2025b）。例如将 “1776 能被 4 整除” 的推理步骤改为 “1776 不能被 4 整除” 后，模型仍可能得出 “1776 年是闰年” 的结论，说明中间推理链仅是模型为迎合人类预期而生成的 “附加装饰”，与结论无实质逻辑关联。

上述发现共同指向一个核心结论：LLMs 并非遵循逻辑规则的 “推理者”，而是擅长模拟推理文本的 “生成器”。但现有研究仍未系统性解答两个关键问题：CoT 推理的失效是否存在可预测的规律？其失效边界与数据特征存在何种关联？

2.3 CoT 推理的能力边界：分布外泛化的核心瓶颈

分布外（Out-of-Distribution, OOD）泛化能力 —— 即对训练数据中未涵盖的问题类型、结构或格式的适配能力 —— 是衡量推理真实性的关键标准，也是 CoT 技术面临的主要瓶颈（Budnikov et al., 2025；Zhang et al., 2024b）。

2.3.1 CoT 泛化能力的表象与实质

早期研究曾显示 CoT 能实现一定程度的 OOD 泛化，例如在多步骤推理任务中适配超出训练长度的推理链（Shen et al., 2025；Yao et al., 2025），但后续研究揭示了其泛化能力的局限性：

• 依赖熟悉模式映射：LLMs 在处理新任务时，会本能地将其映射到预训练阶段接触过的相似任务结构上（Garg et al., 2022；Song et al., 2025）。例如学习新数学函数时，模型更倾向于复用已知函数的推理模板，而非构建新的逻辑体系。

• 泛化效果依赖外部条件：CoT 的泛化性能并非其固有属性，而是高度依赖模型架构与训练设置。Cho 等人（2024）发现，仅当算术规则被编码到模型的位置嵌入中时，CoT 才能在算术任务中实现良好泛化；Wang 等人（2025a）则证实，训练数据中 CoT 示例的精细度直接决定了模型的 OOD 表现。

2.3.2 真正泛化的缺失

当测试任务与训练数据存在本质差异（如全新的推理逻辑、陌生的提问格式）时，CoT 推理会彻底失效（Li et al., 2025a；Wang et al., 2025b）。这一现象进一步支撑了 “CoT 推理本质是模式匹配” 的观点：仅当测试数据与训练数据共享潜在结构时，模型才能通过复用既有推理模板生成合理输出；一旦脱离熟悉的数据分布，模式匹配机制便无从发挥作用。

综合上述研究进展可见，当前学界已完成对 CoT 推理 “表面成功” 的验证、“非真推理” 的质疑及 “泛化薄弱” 的认知，但仍存在关键空白：缺乏从数据视角出发的系统性分析框架，未能清晰拆解 CoT 推理在 “任务类型、推理长度、问题格式” 等维度的失效规律。

基于此，本文以 “数据分布” 为核心视角，将 CoT 推理的 OOD 泛化能力拆解为任务泛化、长度泛化与格式泛化三个维度，通过可控实验环境探究不同分布偏移场景下的失效机制 —— 这一研究设计既回应了现有争议，也为明确 CoT 推理的本质与边界提供了全新分析路径。

3 重新解读思维链（CoT）

一、核心论点：CoT 不是 “推理”，是 “看样学样” 的模式匹配

研究者最关键的主张是：CoT 的本质是 “找规律套模板”，而非执行真正的逻辑推理。 就像人看到 “1+2=3，2+3=5”，记住 “前两个数加起来得第三个数” 的模式，再遇到 “3+5=？” 能答 8，但没真懂 “加法逻辑”—— 如果换成 “1,2,4,？”（翻倍模式），没见过的话就会翻车。 模型的 CoT 也是如此：它在训练数据里记住了 “某种问题该配什么步骤、什么答案” 的统计规律，测试时只要题目和训练数据的 “规律（分布）” 像，就能输出像模像样的推理；一旦规律变了，就露馅了。

二、用 “数学语言” 把论点说清楚

为了让 “模式匹配” 的观点更严谨，研究者用公式定义了三个关键概念，本质是在讲 “模型能不能做好题，全看训练和测试的题像不像”：

训练 / 测试风险：模型 “学没学好” 和 “用得好不好” 的量化

• 训练风险（公式 1）：简单说就是 “模型在训练题上的出错概率”。比如训练时全是 “2 步推理题”，模型做对率 99%，那训练风险就很低 —— 这说明它记住了 2 步题的 “模板”。

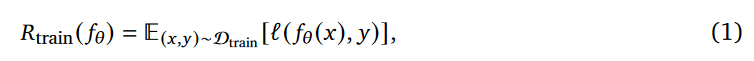
• 测试风险（公式 2）：“模型在新测试题上的出错概率”。如果测试题还是 2 步题，测试风险低；如果换成 3 步题，测试风险就会飙升 —— 因为 “模板” 对不上了。

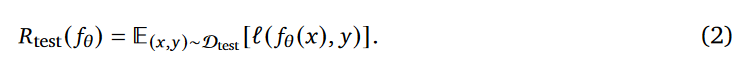
分布差异：“训练题” 和 “测试题” 的 “不像程度”

用 “分布差异（公式 3）” 衡量训练数据（比如全是 2 步数学题）和测试数据（比如全是 3 步数学题）的 “规律差距”。

就像用尺子量两个东西的 “距离”：差距越小（题越像），分布差异值越小；差距越大（题越不一样），值越大。常用的 “尺子” 有 KL 散度、Wasserstein 距离等。

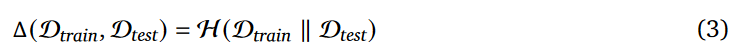
泛化界定理：把 “题像不像” 和 “做对率” 绑死（公式 4 的核心） “模型在测试题上的出错概率（测试风险），取决于三件事”： ① 训练时的出错概率（训练风险）—— 基础没学好，肯定用不好； ② 训练和测试的题的 “不像程度”（分布差异）—— 题越不一样，错得越多（“Λ” 是放大这个影响的系数，比如复杂任务对 “不像” 更敏感）； ③ 训练样本量（n）—— 练得越多，对 “模板” 记得越牢，轻微 “不像” 时容错率稍高。

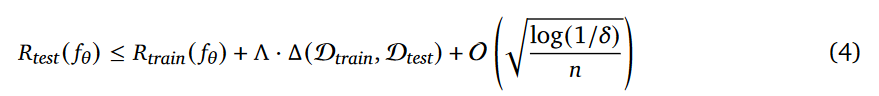
简单说：题越像 + 练得越熟→错得越少；题越不像→再熟也没用。

三、找对 “看题像不像” 的 3 个角度：分布偏移的三大维度

既然 “不像” 会导致 CoT 失效，那 “不像” 具体体现在哪些地方？研究者划分了 3 个最关键的 “变样角度”，也是后续验证观点的核心方向：

任务泛化：“换题型”—— 比如练了加法，考乘法

指 “推理任务的核心逻辑变了”。

例子：训练时只教 CoT 做 “先算加减再算乘除” 的题，测试时换成 “先算乘除再算加减”，或直接考 “解方程”（全新逻辑）。

模型没见过新题型的 “步骤模板”，哪怕输出看起来有模有样的步骤，答案也会错 —— 就像背了 “先乘后加” 的步骤，却套在 “先加后乘” 的题上，步骤对但结果错。

长度泛化：“换步骤长短”—— 比如练了 2 步推理，考 5 步

指 “推理需要的步骤数或题目的复杂程度变了”。

训练数据里的题都是 “2 步推理”（比如 “先找年份→再判闰年”），测试时换成 “4 步推理”（“找年份→看是否整百→查是否被 400 整除→判闰年”）。

模型只会 “凑 2 步模板”，要么漏步骤，要么瞎加无关步骤，根本不会根据 “题的难度” 调整推理长度 —— 就像只会写 50 字作文，让写 200 字就硬凑废话。

格式泛化：“换问法”—— 比如把 “怎么算？” 改成 “结果是？请分步说”

指 “提问的说法、结构变了，但核心问题没变”。

比如原题是 “计算 3+4×2，分步写过程”，测试时改成 “请列出 4 乘 2 再加 3 的计算步骤，求结果”。

模型对 “提问的表面格式” 很敏感，换个说法就认不出 “核心是算混合运算”，因为它记的是 “‘计算… 分步写’对应什么步骤”，没真懂问题本身。

研究者先抛出 “CoT 是模式匹配” 的核心论点→用 “训练 / 测试风险、分布差异、泛化界定理” 三个公式把论点理论化（证明 “题像不像决定对错”）→划分 “任务、长度、格式” 三个维度，明确 “题怎么变会不像”→最后说 “接下来会用实验验证：这三个维度变了，CoT 肯定翻车”，为后续实验做铺垫。

4 什么是DataAlchemy

一、先搞懂核心目的：DataAlchemy 是个 “排除干扰的实验箱”

想知道 CoT 是 “真推理” 还是 “套模板”，用真实数据测试就像 “在菜市场测视力”—— 环境太乱（数据里藏着无数未知规律），就算模型做对题，也说不清是懂了逻辑还是碰巧见过类似题。 所以研究者造了DataAlchemy 这个 “无菌实验箱”：所有 “题目”（任务）、“素材”（数据）、“规则”（推理逻辑）全是人工定义的，没有一点真实世界的杂乱干扰。 就像想测 “人是不是靠记公式做题”，不考复杂数学题，而是自己编一套 “用 A、B、C 按固定规则变形” 的题 —— 先只教 “规则 1”，再考 “规则 2”，如果立刻翻车，就说明是记模板而非懂逻辑。DataAlchemy 干的就是这事，专门精准测试 CoT “换规则就露馅” 的特性。

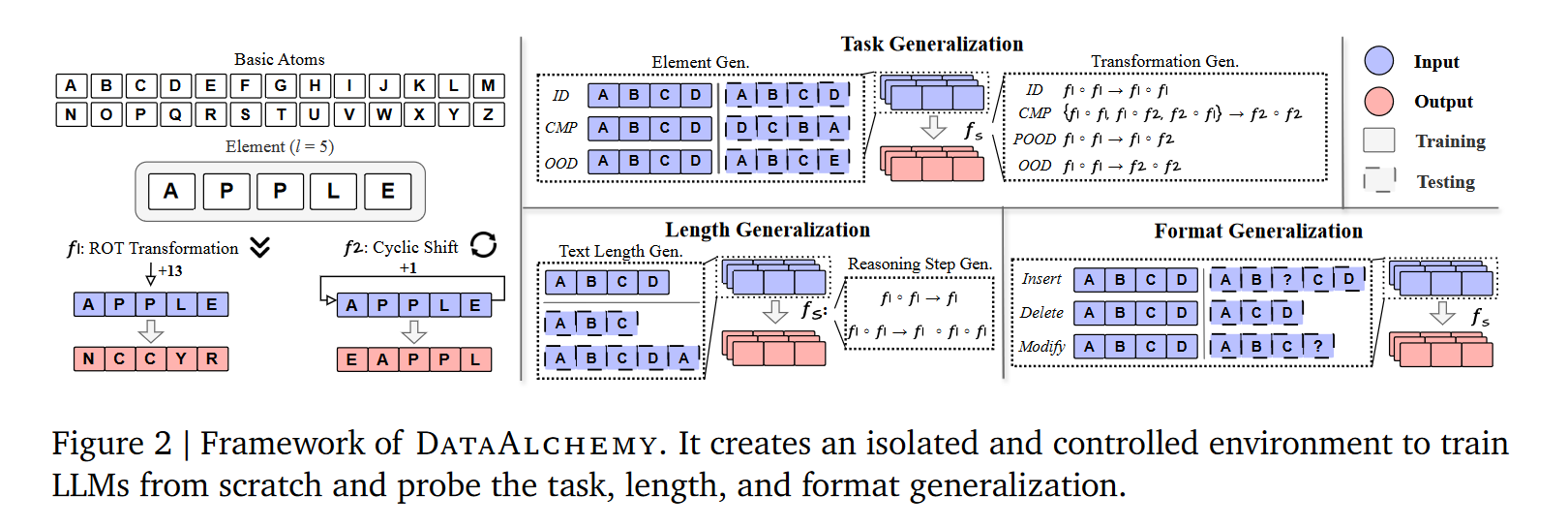
二、拆解 “实验箱” 的 3 个核心部件：素材、规则、测试条件

素材：用 “字母积木” 搭任务 —— 基础原子与元素

这是构成所有 “推理题” 的原材料，简单到不会有歧义：

• 原子：就是 26 个英文字母（A-Z），相当于搭积木的 “小方块”。

• 元素：把字母按顺序排成一串，比如 “(A,P,P,L)” 就是一个 “4 块积木的造型”（元素长度l=4）。 为啥这么设计？① 积木数量（l）能随便调，比如l=4时有 26×26×26×26=45 万多种造型，足够喂给模型学；② 想测 “能不能处理更长 / 更短的题”，直接改l就行（比如练l=4，考l=5），精准又方便。

规则：用 “变形玩法” 造推理题 ——3 类变换操作

“变换” 就是让 “字母积木造型” 变样的规则，相当于 CoT 要解的 “应用题”。3 类变换层层递进，专门模拟 “多步推理”：

• ① ROT 变换：单个积木 “变脸” 规则：每个字母按字母表往前 / 后挪n位（超 26 位循环），比如 A 挪 13 位变 N，P 挪 13 位变 C。 类比：就像给积木涂颜色的固定公式 ——“红色积木涂 13 下变蓝色”，步骤单一，容易学但也容易记死。

• ② 循环位置偏移：积木 “整体挪位” 规则：整串字母往右挪n位，最右边的 “积木” 移到左边补位。比如 “(A,P,P,L)” 挪 1 位变 “(L,A,P,P)”。 类比：把一排积木往右推 1 格，最右边的放左边，是另一种完全不同的 “变形逻辑”。

• ③ 复合变换：串起多个玩法 —— 模拟 “多步推理” 规则：把前两种变换按顺序组合，比如 “先变脸（ROT13），再挪位（偏移 1）”，就成了 “2 步推理题”。 关键是：这个过程能自动拆出 “CoT 步骤”—— 比如 “(A,P,P,L)→(N,C,C,Y)（ROT13）→(Y,N,C,C)（偏移 1）”，前半部分是推理步骤，最后是答案，不用人工写步骤，直接给模型当训练素材。 类比：先按 “公式 1” 变一次，再按 “公式 2” 变一次，模型要学的就是 “两步公式的顺序和用法”。

测试条件：保证实验 “公平可信”—— 环境配置

为了让测试结果靠谱，研究者把 “实验箱” 的条件卡得很死，同时留好 “变量” 验证结论：

• 固定条件：用小参数的 GPT-2 模型（避免 “靠记忆力碾压”），推理时输出固定（排除 “瞎蒙碰对”），默认用 4 个字母的元素（统一初始难度）。 就像测记忆力不找学霸，找普通人，且不让瞎猜，保证变量只在 “规则变不变” 上。

• 变量测试：后续会换大模型、调参数、改字母长度，确保 “CoT 靠套模板” 的结论不是偶然，换任何模型都一样。

• 评分标准：不只看 “答案对不对”，还看 “步骤对不对”（完全匹配率）、“和正确结果差多少”（编辑距离），避免 “步骤瞎写却蒙对答案” 的误判。

5 任务泛化

一、核心目标：测试 CoT 能否 “举一反三”

“任务泛化” 本质是问：模型学了一种 “玩法”（比如用规则 A 变字母），遇到没见过的 “新玩法”（新规则）或 “新棋子”（新字母），还能做好吗？

这是判断 “真推理” 还是 “套模板” 的关键 —— 人懂逻辑能举一反三，而只会套模板的模型换个场景就翻车。研究者把任务泛化拆成两类：“元素泛化”（换棋子）和 “变换泛化”（换玩法），分别做实验。

二、先立 “衡量标准”：任务泛化复杂度（TGC）

为了精准说清 “新任务有多难”，研究者定义了一个 “难度公式”（Proposition 5.1），核心逻辑很简单：

新东西越多，难度越高，CoT 越容易错。

公式里的关键项翻译过来就是：

• 新字母（元素）越多 → 难度加一分；

• 新变换规则（比如没学过的 ROT 参数）越多 → 难度加一分；

• 新的变换组合顺序（比如学了 “先 ROT 再挪位”，考 “先挪位再 ROT”） → 难度加一分。

更关键的是 “失败阈值定理”（Theorem 5.1）：一旦难度超过某个临界点（τ），CoT 做对的概率会 “断崖式下跌”，像从楼梯上摔下来一样快 —— 这说明模型根本没法 “慢慢适应新规则”，只能靠死记硬背旧模板。

三、核心实验 1：变换泛化 —— 换 “玩法” 就露馅

“变换泛化” 测试模型遇到 “新规则 / 新规则组合” 时的表现。研究者设计了 4 种难度递增的场景，用之前 DataAlchemy 的 “ROT 变换” 和 “位置偏移” 做实验：

4 种测试场景（从 “眼熟” 到 “全新”）

场景	通俗解释（以学过 “先 f₁再 f₂” 为例）
分布内（ID）	考的和学的一模一样：“先 f₁再 f₂”→ 考 “先 f₁再 f₂”
组合（CMP）	规则眼熟但组合新：学过 f₁、f₂，考 “先 f₂再 f₂”
部分分布外（POOD）	混入一个新规则：学过 f₁，考 “先 f₁再新规则 f₃”
完全分布外（OOD）	全是新规则：学过 f₁，考 “先 f₃再 f₄”

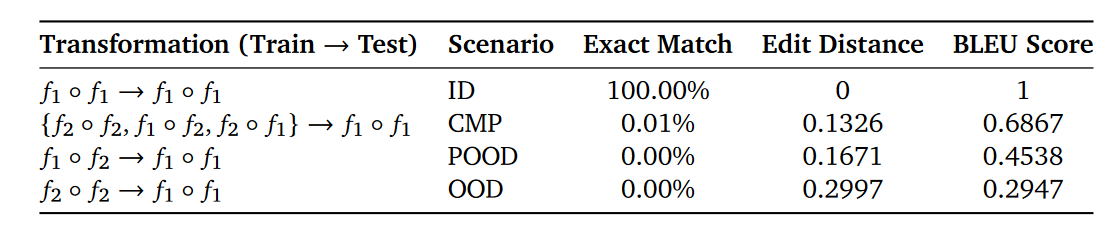
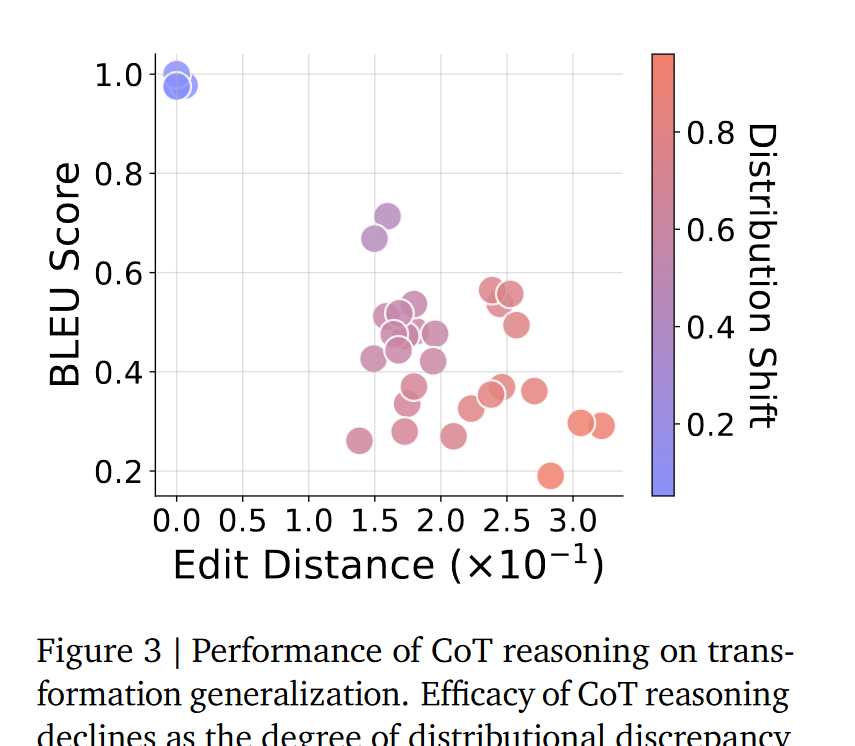
实验结果：除了 “原题”，全翻车

• 正确率暴跌：ID 场景正确率 100%，CMP 直接跌到 1%，POOD 和 OOD 全是 0%；

• 迷惑性细节：模型偶尔会输出 “看起来超对的推理步骤”，但答案错得离谱。比如学了 “先 ROT13 再挪位”，考 “先挪位再 ROT13” 时，模型还按旧步骤写，但算出来的字母全错 —— 这就是典型的 “套步骤模板，不懂逻辑”；

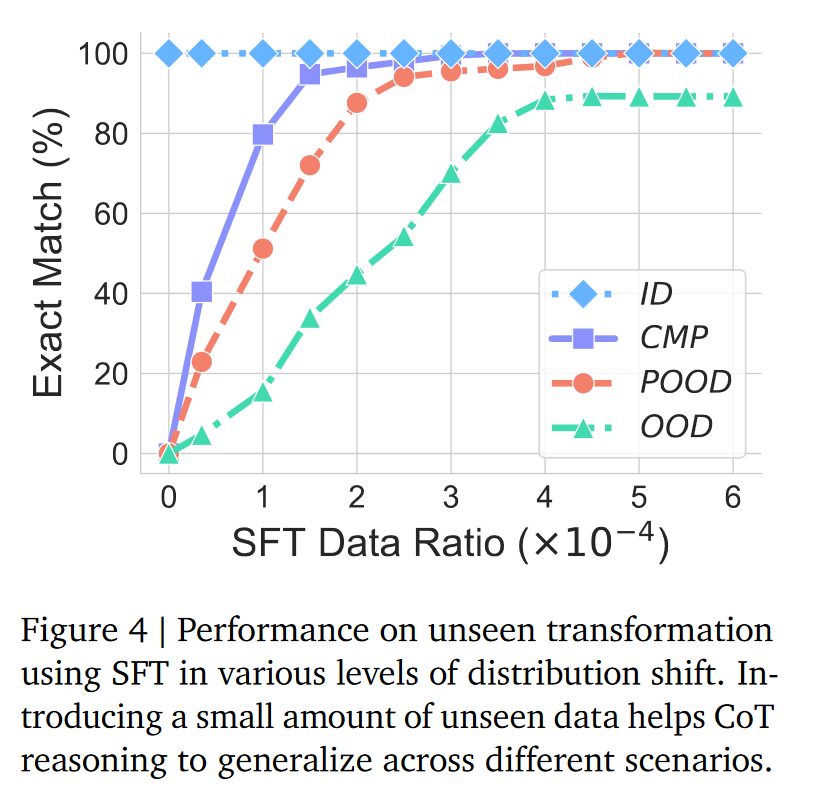
• 微调也救不了：给一点新数据微调（SFT），模型能快速适应新规则，但本质是 “多记了个新模板”，不是真懂逻辑 —— 换个没微调过的新规则，照样翻车。

四、核心实验 2：元素泛化 —— 换 “棋子” 就懵圈

“元素泛化” 测试模型遇到 “新字母组合” 或 “完全没见过的字母” 时的表现，同样设计了 3 种场景：

3 种测试场景

场景	通俗解释（以学过 “(A,B,C,D)” 为例）
分布内（ID）	考一样的字母组合：“(A,B,C,D)”→ 考 “(A,B,C,D)”
组合（CMP）	字母眼熟但顺序新：学过 A、B、C、D，考 “(B,C,D,A)”
完全分布外（OOD）	字母全没见过：学过 A-D，考 “(X,Y,Z,W)”

实验结果：比变换泛化更惨

• 正确率直接归零：从 ID 到 CMP、OOD，正确率从 100% 跌到 0%，连文本相似度（BLEU 分数）都成了 0—— 模型甚至写不出有效字母，直接 “卡壳”；

• 微调效果有限：给新字母组合微调后，只有 “和学过的组合很像”（比如编辑距离 n=1，只差一个字母顺序）时才有点用，一旦差异稍大（n=3），正确率就跌到谷底，说明模型根本没法 “理解字母是可替换的元素”，只能记固定组合。

五、总结：任务泛化实验的核心结论

• CoT 没有 “举一反三” 的能力：无论是换 “玩法”（新变换）还是换 “棋子”（新元素），只要和训练时的 “模板” 不一样，CoT 就失效；

• “步骤对答案错” 是关键证据：模型能模仿推理的 “形式”，却抓不住 “逻辑本质”，进一步证明 CoT 是 “模式匹配”；

• 微调只是 “加模板”：给新数据微调只能让模型多记几个新模板，解决不了 “不会真推理” 的根本问题 —— 就像学生背了更多题，但没懂公式，换个题型还是不会。

6 长度泛化

一、核心问题：CoT 能 “适配不同长短的任务” 吗？

“长度泛化” 本质是问两个关键问题：

• 学了 “4 块积木的造型”（固定长度的输入文本），遇到 3 块、5 块的造型还能处理吗？（文本长度泛化）

• 学了 “2 步搭好积木”（固定步骤的推理），遇到 1 步、3 步的搭建要求还会做吗？（推理步骤泛化）

这就像判断一个人是 “真懂搭积木逻辑” 还是 “只背了固定造型的步骤”—— 真懂的人能根据积木数量调整步骤，只背模板的人多一块、少一块就会乱套。CoT 的表现显然是后者。

二、先立 “规律”：长度差越大，CoT 错得越离谱

为了精准描述 “长度变化对 CoT 的影响”，研究者提出了 “长度外推的高斯衰减” 规律（命题 6.1），通俗说就是： 测试任务的长度和训练时的长度差得越多，CoT 的错误率就越高，而且是 “越差越远，错得越快”。

就像投篮时偏离篮筐越远，投中的概率下降得越快 —— 模型只在训练的 “固定长度”（比如 4 个字母、2 步推理）上 “投得准”，稍微偏离就 “脱靶”，且偏离越多，错得越彻底。

三、两大实验：文本 / 步骤长度一变，CoT 立刻露馅

• 文本长度泛化：换 “积木数量”，就瞎增瞎减凑数

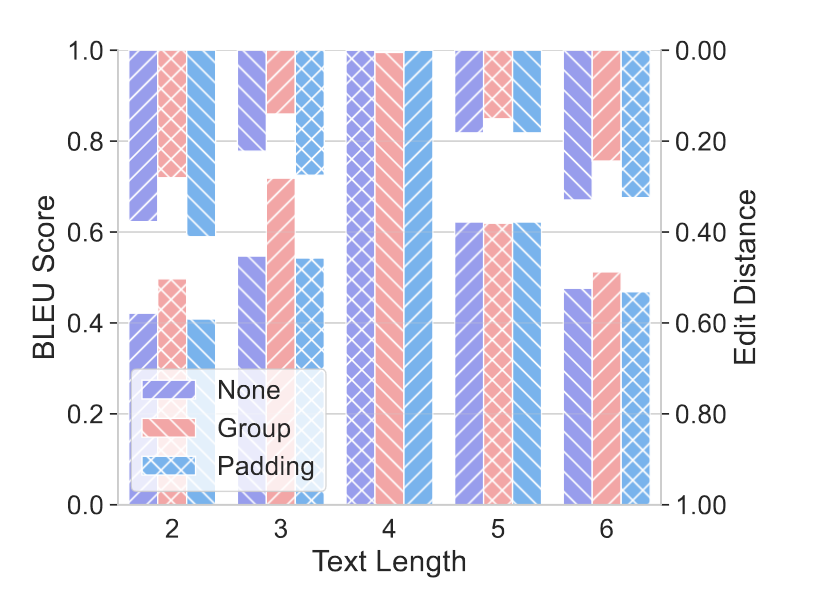
“文本长度” 指输入的字母序列长短（比如l=4是 4 个字母，l=5是 5 个字母），实验专门测试模型能否适配不同长度的输入。

实验设计：

• 训练：只练l=4（4 个字母的元素），搭配 3 种 “应对长文本” 的策略（不处理、补空字符、拆分文本）；

• 测试：用l=3（少 1 个字母）、l=5（多 1 个字母）的元素考模型。

结果：越不像训练模板，错得越狠

• 正确率暴跌：从l=4的满分（BLEU=1），跌到l=3的 0.55、l=5的 0.62，轻微差异就明显翻车；

• 搞笑操作：模型会 “硬凑长度”—— 遇到l=3就瞎加一个字母，遇到l=5就瞎删一个，非要改成训练时的 4 个字母长度，完全不管逻辑对不对；

• 策略没用：补空字符的方式完全无效；拆分文本稍有用，但只是 “让模板适配更灵活”，没解决 “不懂长度逻辑” 的根本问题。

• 推理步骤泛化：换 “搭建步骤”，直接不会做

“推理步骤长度” 指完成任务需要的操作步数（比如k=2是 2 步变换，k=3是 3 步变换），测试模型能否应对不同步骤的推理需求。

实验设计：

• 训练：只练k=2（2 步变换，比如 “先 ROT 再挪位”）；

• 测试：用k=1（1 步）、k=3（3 步）的推理题考模型，还试了 “加少量新步骤数据微调” 的效果。

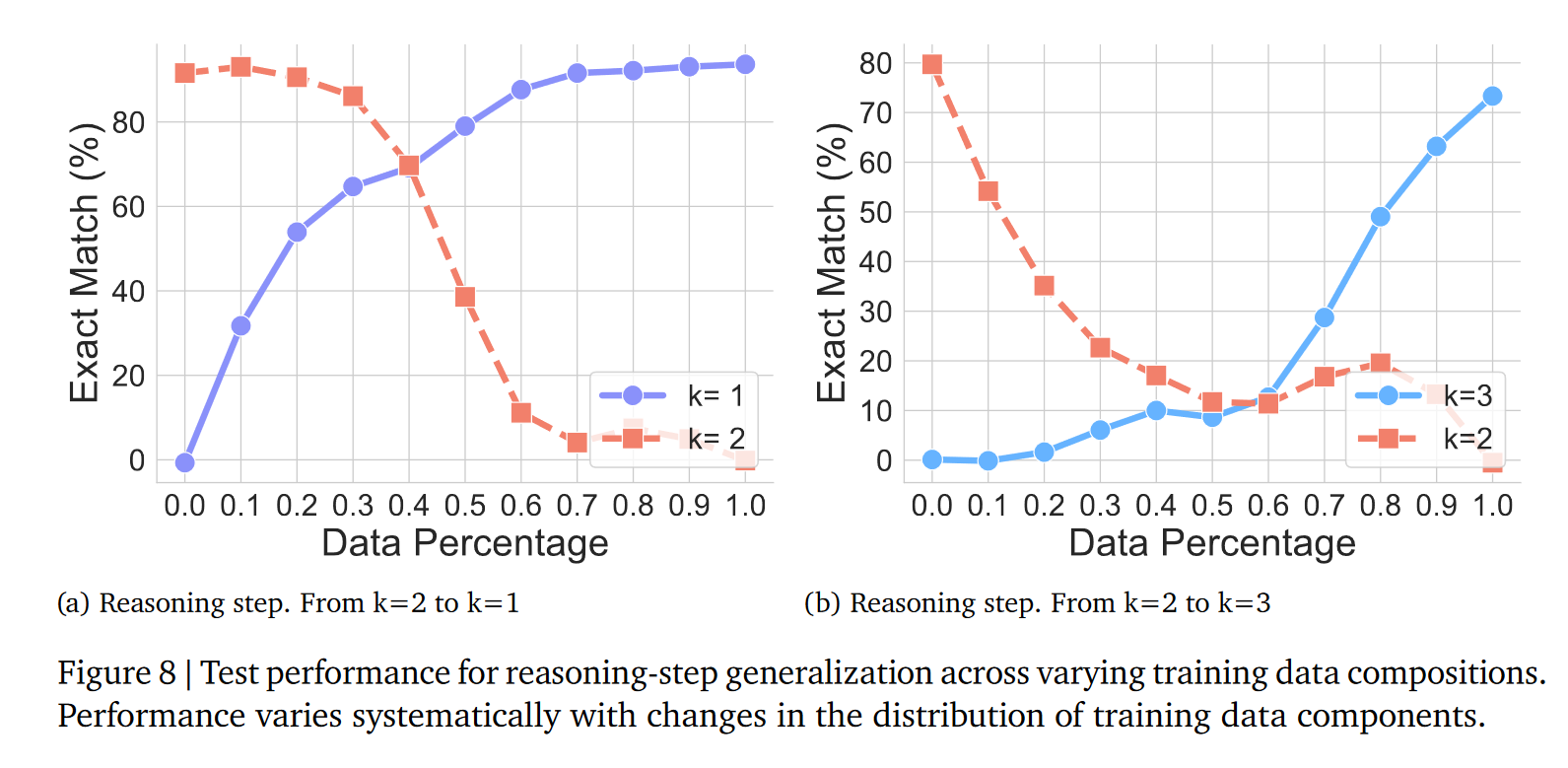
结果：步骤不对就躺平，微调也顾此失彼

• 直接失效：k=1和k=3的题全做错，完全无法泛化；

• 微调治标不治本：加少量k=3的数据微调，模型能做对k=3的题，但原来会的k=2题反而做错了 —— 因为模型只是 “多记了个k=3的模板”，不是真懂 “步骤可多可少” 的逻辑，学新模板就忘了旧模板；

• 印证核心假设：只有 “训练里有类似步骤长度的模板”，模型才会做，否则必错，彻底坐实 “模式匹配” 本质。

四、总结：长度泛化实验的核心结论

• CoT 是 “长度绑定” 的模板怪：只认训练时的 “固定长度”（文本长短、步骤多少），偏离就失效，且偏离越多错得越彻底；

• 没有 “灵活适配” 能力：遇到不同长度不会 “调整逻辑”，只会 “硬凑模板”（增删字符、死记新步骤），暴露了 “不懂推理本质”；

• 微调救不了：微调只是 “加新模板”，无法让模型学会 “适配长度的逻辑”，反而可能忘旧模板，本质还是 “记多少会多少，没记就不会”。

简言之，CoT 就像只会画 “4 厘米直线” 的机器人 —— 画 4 厘米很标准，画 3 厘米就多画 1 厘米，画 5 厘米就少画 1 厘米，完全不懂 “直线长度可以灵活调整”，只因没记过其他长度的 “画法模板”。

7 格式泛化

一、核心目标：解决 “模型会不会死记模板” 的问题

评估思维链（CoT）推理的 “抗格式干扰能力”—— 判断模型是能灵活应对不同查询格式，还是只依赖训练时的固定表述（比如换个提问话术就失效）。

二、关键工具：用 “格式对齐分数（PAS）” 测相似度

• 作用：衡量测试查询与训练模板的像似度，值越高说明测试格式越贴近训练场景；

• 原理：把每个查询（训练 / 测试）转成 “向量”（计算机可识别的 “标签”），找训练集中与测试向量最像的那个，相似度就是 PAS。

• 价值：PAS 低的测试场景，才能真正考验模型的泛化能力。

三、实验设计：故意 “搞乱” 格式，测模型抗干扰性

• 4 种 “搞乱” 方式（模拟真实场景）：

  • 插入：加无意义内容（如 “1+1” 变 “#1# + #1#”），模拟噪声 / 冗余；

  • 删除：删部分词（如 “请计算 1+1” 变 “计算 1+1”），模拟表述不完整；

  • 修改：换无意义内容（如 “请计算” 变 “请 @#￥”），模拟错字 / 替换词；

  • 混合：组合以上多种方式，模拟复杂混乱。

• 控制变量：用概率 p（如 20%）控制 “搞乱” 的程度，看模型在不同混乱度下的表现。

四、核心结论与实用价值

结论：

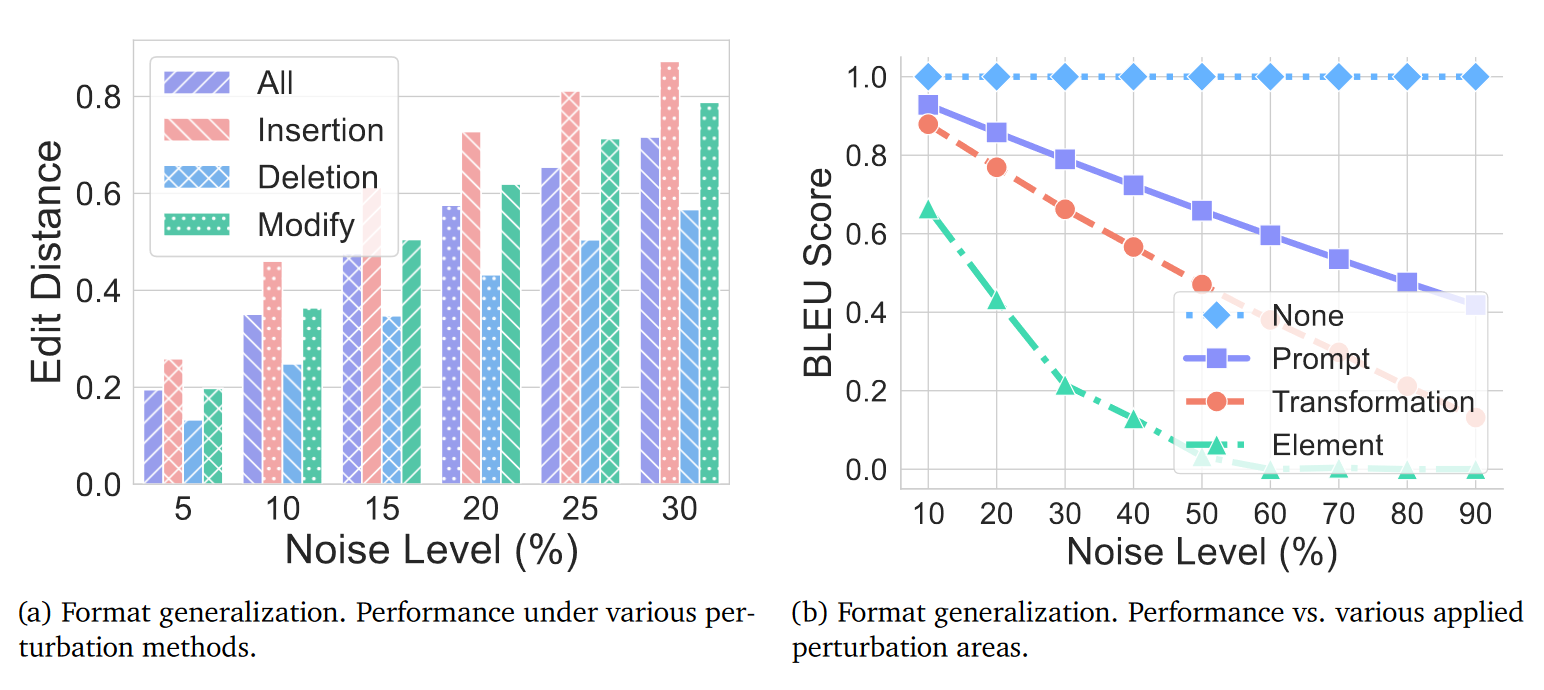
• 模型对格式变化很敏感，其中 “插入噪声” 影响最大（加乱码最易让模型出错），“删除内容” 影响最小（少个词影响不大）；

• 查询里的 “核心信息”（如数学题的 “1”“+”）和 “推理要求”（如 “计算”“比较”）是关键 —— 这两部分格式乱了会影响结果，其他部分（如 “请”“麻烦”）怎么改都没事。

价值（指导模型优化）：

• 训练时多加入 “带噪声的查询”，提升模型抗干扰能力；

• 重点保证 “核心信息” 和 “推理要求” 的格式稳定，减少无效格式干扰。

8 采样温度 和 模型规模

一、研究要解决的核心问题

大语言模型做 “思维链推理”（比如分步算题、逻辑分析）时，两个关键因素 ——采样温度（控制输出随机性）和模型规模（参数量大小）—— 会不会影响推理的稳定性和准确性？研究就是要搞清楚这两个因素的作用。

二、第一个因素：采样温度的影响

先搞懂 “采样温度” 是什么？

可以把它理解为 “模型输出的‘放飞程度’”：

• 温度低（比如 1e-5，接近 0）：模型很 “保守”，输出重复、确定（比如问 10 次 “1+1”，都答 “2”）；

• 温度高（比如 1）：模型稍 “灵活”，输出可能有轻微变化（但不会离谱，比如不会答 “3”）；

• 温度超 1 太多：模型会 “乱答”（比如答 “1+1 = 月亮”）。

• 实验怎么测？

用和之前 “变换泛化” 实验完全一样的配置，只改 “温度” 这个参数，看结果会不会变。

• 结论很省心：温度在 “1e-5 到 1” 之间，模型很稳定！

不管温度是低（比如 0.1）还是高（比如 1），只要在这个区间内：

• 模型推理的结果都一致、可靠（不会因为温度变一点就答错题）；

• 就算测试场景和训练场景不一样（比如训练时算加法，测试时算减法），这种稳定性也不会破。

对我们的用：不用纠结温度的 “精确值”！

调参时不用反复试 0.2、0.3 这种细微差别，只要设为 1e-5 到 1 之间的任意值（比如默认 0.7），效果都差不多，省了很多调参功夫。

三、第二个因素：模型规模的影响

• 先搞懂 “模型规模” 是什么？

就是模型的参数量（比如 10 亿参、50 亿参、100 亿参），一般人会觉得 “参数量越大，模型越厉害”。

• 实验怎么测？

分两步，保证公平：

① 先给不同规模的模型做 “预训练”（用同一套任务，比如都是 “两次变换计算”）；

② 再给它们做 “监督微调”（用另一套任务，比如都是 “另一种两次变换计算”），同时还会改 “微调数据占比”（比如用 10%、30%、50% 的微调数据）。

• 结论反常识：模型规模不影响推理 accuracy！

不管模型是小（10 亿参）还是大（100 亿参），也不管微调数据用得多还是少：

• 它们的推理准确率，和 “默认规模的模型”（实验时用的基准模型，比如 50 亿参）几乎一样。

对我们的用：不用盲目追 “大模型”！

不用花大价钱用超大参数量的模型（算力成本高），用基准规模的模型（比如实验里的默认模型），只要好好微调，就能达到一样的推理效果，又省钱又省算力。

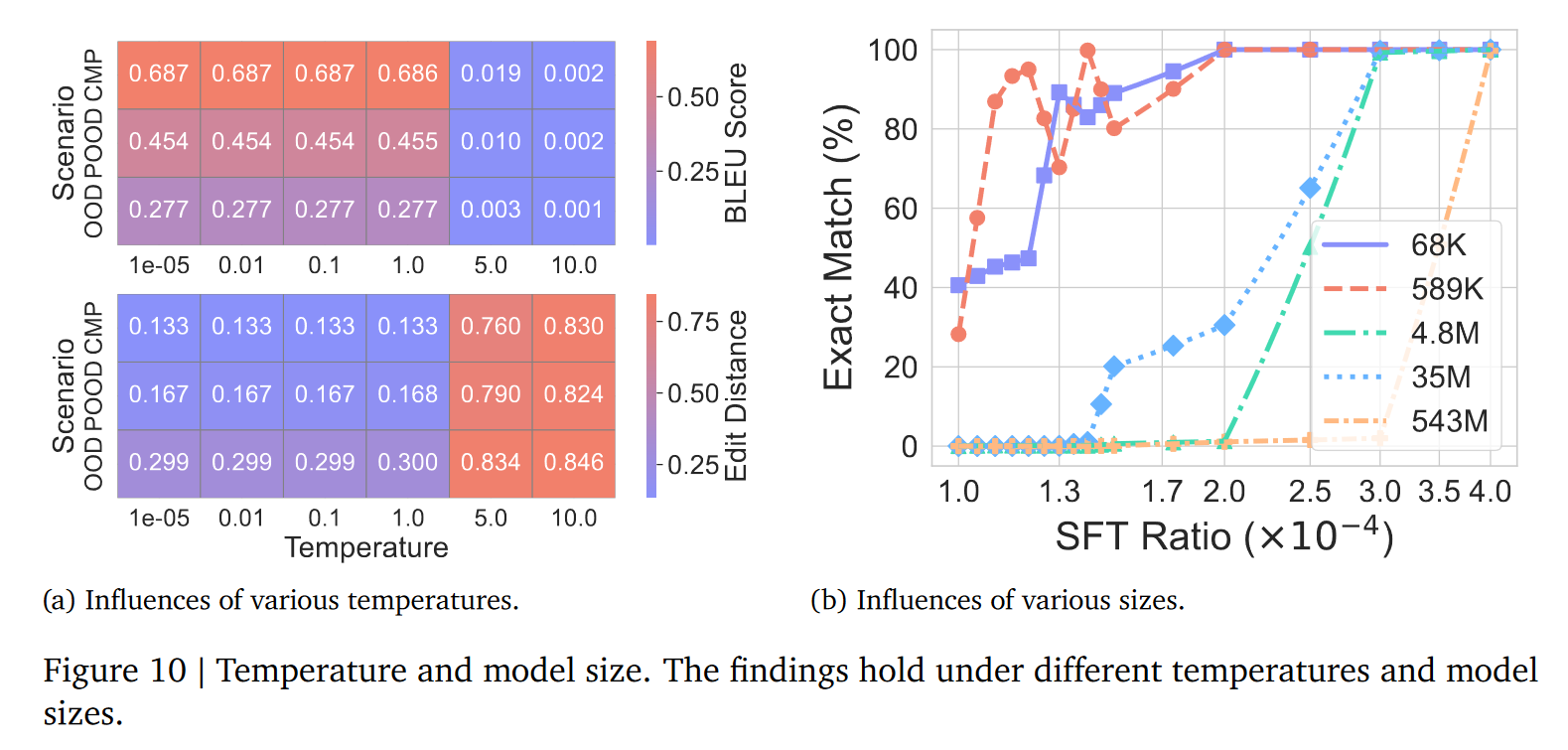
四、总结：两个 “不用”，轻松用模型做 CoT 推理

• 不用纠结 “温度调多少”：1e-5 到 1 之间随便设，效果都稳定；

• 不用盲目追 “大模型”：基准规模的模型微调好，就能打，成本还低。

这两个结论让模型的实际应用更简单、更经济。

9 实验观点

一、研究的核心颠覆结论：CoT 推理没那么 “智能”

通过 “DataAlchemy” 这个可控实验环境的研究发现：

大语言模型的 “思维链推理（CoT）” 看似厉害，其实更像个 **“脆弱的幻象”**—— 它并不是真的在做逻辑推理，而是在玩 “高级版结构化模式匹配”：

• 本质：靠记住训练数据里的 “句式、步骤模板” 来生成推理链，跳不出训练过的数据范围；

• 弱点：只要测试场景稍微偏离训练数据（比如换个没见过的题、改个表述），推理准确率就会大幅下降，暴露其 “推理” 只是表面功夫的本质。

通俗说：CoT 就像只会背 “解题模板” 的学生，换个没见过的题型就懵了，不是真的懂逻辑。

二、结论能推广到 “大模型” 吗？

能！虽然实验用的是 “从零训练的模型”，但研究发现的规律对 “大规模预训练模型”（比如 GPT、LLaMA）同样适用 —— 不管模型多大多强，CoT 的 “模式匹配本质” 没变，偏离训练数据就容易出错。

三、对实际应用的 3 条关键启示（给从业者的建议）

别过度依赖 CoT，警惕 “虚假靠谱感”

• 核心提醒：别把 CoT 当 “即插即用” 的万能推理工具，尤其在医疗（看病诊断）、金融（投资分析）、法律（案件判断）等 “高风险领域”；

• 为什么？模型会生成 “流畅的废话”—— 推理链读起来很通顺、像那么回事，但逻辑上是错的（比如给病人误诊却理由充足），这种 “假靠谱” 比 “直接答错” 更危险（容易让人信以为真）；

• 怎么做？必须让领域专家做充分审核（比如医生再核对模型的诊断建议），不能全靠模型拍板。

例子：模型给癌症患者推荐错误治疗方案，但推理步骤写得头头是道，若医生不审核，后果不堪设想。

别只测 “相似数据”，重点做 “跨界测试”

• 问题：现在很多测试只用水准和训练数据差不多的 “相似题”（比如训练算 “1+2”，测试算 “3+4”），测不出 CoT 的真实抗干扰能力；

• 怎么做：必须做 “对抗性测试” 和 “跨界测试（OOD 测试）”—— 故意设计 “偏离训练数据” 的场景，比如：

  • 任务跨界：训练算数学题，测试做逻辑推理；

  • 长度跨界：训练短文本推理，测试长文章分析；

  • 格式跨界：训练 “问句式” 查询，测试 “命令式” 查询；

系统地找出模型的薄弱点。

别把 “微调（SFT）” 当 “万能药”

• 实验发现：微调（给模型喂新数据，让它适应新场景）能快速 “修补” 模型在某类新数据上的表现（比如微调后能算新题型了）；

• 但要注意：这不是 “真的学会了泛化”，只是把模型的 “能力范围” 稍微扩大了一点（比如从 “会算加法” 扩展到 “会算加减”），没解决 “不会抽象推理” 的核心问题；

• 警示：靠微调来解决所有 “跨界出错” 的问题，是治标不治本的笨办法 —— 新场景永远比微调的范围多，迟早会遇到新的 “不会的题”，不可持续。

通俗说：微调就像给学生补 “新题型”，补一个会一个，但没教逻辑思维，遇到没补过的题还是不会。

四、总结：用 CoT 的正确心态

CoT 是个 “好用的工具”，但不是 “智能的推理者”—— 用它时要：

• 不迷信：知道它会出错，尤其在高风险场景；

• 严测试：多测跨界场景，摸清它的能力边界；

• 补人力：让专家审核结果，别让模型独断。

只有这样，才能安全、有效地发挥 CoT 的价值。