CGAL Kernel设计 翻译

CGAL《An Adaptable and Extensible Geometry Kernel》翻译

1 Introduction

处理固定大小几何对象（如圆、直线、点等）的几何算法通常与它的特定表示形式无关。假定这些几何对象上定义了某些操作和简单谓词（谓词predicates，的含义是对几何对象的基本操作，例如判断平面上3个点v0、v1、v2是顺时针还是逆时针。像这样的基本操作会被上层算法频繁使用）。例如：用于比较两个对象或确定它们的相对位置的简单谓词。算法用这种方式描述是因为就算法的正确性而言，几何对象的所有表示都是同样有效的。此外，当算法以这种更通用的方式描述时，它们可以被更简洁地描述，更容易被阅读，且适用于许多不同场景。
在实现算法时，我们可以通过将对象的表示、对象的操作和谓词封装到Kernel中来实现同样的优势。算法只通过内核中定义的操作与几何对象交互。这意味着一个算法的实现可以用于相同几何对象的许多不同表示。因此，可以根据应用场景选择最适当的表示(例如，最稳健或最高效的)。
适应性：例如，对于某些场景，可能希望在执行算法期间额外保存每个点的附加信息，或者希望在某个三维共面点集上应用某个二维算法。这两件事都很容易完成：如果相关算法以一种通用的方式实现（通过内核与对象交互），并且内核允许重新定义类型和操作，也就是说，内核很容易适应。
内核的可扩展性同样重要，因为有些应用不仅需要修改现有的对象和操作，还需要添加新的对象和操作。
尽管适应性和可扩展性是值得努力追求的重要目标，但我们不愿意接受在内核上的任何效率损失。实际上，使用模板编程技术可以在不牺牲运行时性能的情况下实现泛型，缺点是它增加了编译时的开销。
下面第2节，讨论了以前关于几何内核设计的工作。第3节，对新内核概念进行大致描述。然后，在4~7节，我们将描述如何在泛型编程范式下以一种可适应和可扩展的方式实现这个概念。第8节演示了这种内核的使用，并展示了上述实现有哪些优点。最后，第9节，我们将描述CGAL中提供的这类内核的几个模型。
由于我们的实现是用c++实现的，我们假定读者对这种语言有些熟悉。[30]提供了c++模板编程的一般介绍，c++模板编程在我们的设计中被广泛使用。Kernel的部分设计灵感来自于STL。

2 Motivation and Previous Work

在过去的10年里，已经开发了许多几何库，每个库都有自己的几何内核概念。c++库PLAGEO和SPAGEO[17]使用浮点算术、类层次结构和公共基类为2维和3维对象提供内核。c++库LEDA[23]在其几何部分中提供了两个内核，一个使用精确有理算法，另一个使用浮点算法。Java库GEOMLIB[3]提供了一个以分层方式构建并围绕Java接口设计的内核。没有一个解决了易于扩展和适应性强的问题。
灵活性是计算几何算法库CGAL（the Computational Geometry Algorithms Library）的基石之一，该库正在欧洲和以色列的几所大学和研究机构的一个共同项目中开发。资料[15]概述详细介绍了库中的功能、设计和实现技术。泛型编程是用来实现这种灵活性的工具之一[7,24,25]。
在CGAL[14]的几何内核的原始设计中，每个几何对象都由一个表示类参数化，而表示类又由一个数字类型参数化。这种设计提供了简单的适应性、扩展性。然而，该设计不允许将表示类扩展为也包括几何操作(operation)。在将几何traits类引入库之后，这种扩展被认为是可取的，它将算法或数据结构的组合部分从底层几何中分离出来。traits类这个术语最初是由Myers[26]提出的;我们在这里用它来指代聚合了(几何)类型和操作的类。通过提供不同的traits类，同一算法可以应用于不同类型的对象。因此，trait类的使用在库的更高级别上带来了更多的灵活性。
由于核（kernel）通常被认为代表几何计算的一组基本构建块，因此很自然地假设Kernel本身可以用作许多算法的trait类。这意味着核的概念不仅必须包括对象的表示，还必须包括对这些对象的操作(operation)，并且，为了获得最大的灵活性，两者都应该易于适应。将不同算法的traits类中的公共需求提取到内核中，对于维护跨库的统一接口和最大化代码重用非常有帮助。

3 The Kernel Concept and Architecture

几何内核由（表示几何对象的）类型(type)和对这些类型的操作(operation)组成。在CGAL的实现中，从c++的角度来看两者都是类（在CGAL代码中，“操作”是重载了operator()的类），但我们仅将前者称为(几何)类型，而将后者称为(几何)操作。这里我们根据内核为每个类型和操作提供的接口来描述内核的概念。
取决于不同的角度，这些类型和操作的预期接口看起来会有些不同。从程序员的角度来看，类型作为独立类出现，而操作作为全局函数或这些类的成员函数出现是很自然的。

然而，从实现算法的人的角度来看，类型和操作都是由内核提供的，才是最自然的。这样封装允许以相同的方式调整和改变类型和操作（比如把kernel从高精度计算换成用double计算）。

上面的c_line和less_xy就是两个函数对象，一个用来构建Line_2，一个用来比较两个点。这less_xy函数对象需要通过调用函数less_xy_2_object()来获取，原因下面会讲到。
我们在这里介绍的内核的概念需要包括这两个角度。也就是说，每个操作（operation）需要同时表示为一个类型(其实例可以像函数一样使用)和 全局函数或成员函数。下面三个部分描述的技术允许这两种接口以最小的维护开销得以共存，从而得到一个所有人都满意的内核。
我们的内核由三层组成，如图1所示。底层由基本的数值原语组成，例如计算矩阵行列式和从点坐标构造直线方程。这些数字原语在第二层的几何原语中会被使用。顶层则融合这些几何原语。我们的kernel的概念的表达范围是与表示无关的仿射几何。例如，用两条线求交构造一个新点就属于该概念，而从x，y坐标构造一个点就不属于该概念。

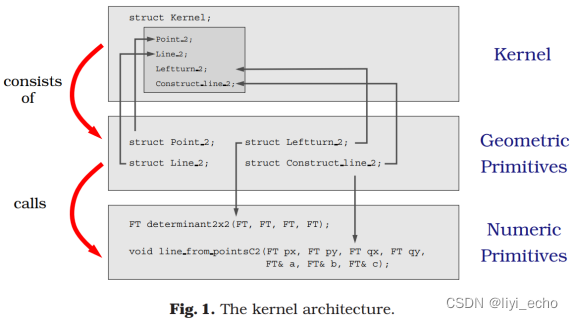
4 An Adaptable Kernel

我们使用一个简化的示例kernel来展示我们的技术。如下图，考虑类型Line_2和Point_2分别表示二维直线和点，一个操作Construct_Line_2从两个Point_2参数构造一个Line_2，一个操作Less_xy_2按字典顺序比较两个Point 2对象。MyPoint、MyLine、MyConstruct和MyLess类是任意的，在别处定义。

第一个问题可能是:Construct_line_2必须从两个point_2构造一个Line_2，因此，它必须对两种类型都有所了解。这要怎么做到？因为我们讨论的是自适应性，所以仅仅将名称MyPoint和MyLine硬连接到MyConstruct中并不是我们想要做的。
一个自然的解决方案是用其他类参数化MyConstruct，例如，用我们的kernel。一旦该类知道了它所在的kernel，它也就知道了所有相关的类和操作。实现此参数化的一种直接方法是将kernel作为模板参数提供给几何类。

这样，上面我们的kernel类就需要做相应的修改了：

起初，这可能看起来有点笨拙;将一个类插入到它自己的组件中似乎会创建循环引用。的确，正如下面的例子所示：

对K::B的引用将导致P::B，并进一步到K::A，但该类型还没有在行*中声明。K类的问题来自这样一个事实:P::B在它自己的定义中指回了K自己，指向仍然未定义的类型K::A。
暂时先不管循环引用的问题，让我们回到主题上来：适应性。当想要扩展或改编这个kernel时，也不难。实际上，从kernel派生一个新类就行了。在这个类中可以添加新的类型定义，并可以修改现有的类型定义。

这里把Point_2修改为了一个不同的类型，并且定义了一个新类型Left_turn_2。用这个New_kernel编程：

令我们惊讶和愤怒的是，最后一行编译报错。

哪里出问题了？问题在于编译器看到的是MyConstruct，而我们希望这里是MyConstruct<New_kernel>。另一方面，这并不令人惊讶，因为我们并没有将类型Construct_line_2修改为New_kernel，因此，它还保持为Kernel，即MyConstruct。MyConstruct<>使用的是类型Kernel::Point_2(=MyPoint)，因此不能接受New_kernel::Point_2(=NewPoint<New_kernel>)参数。由此导致了错误。

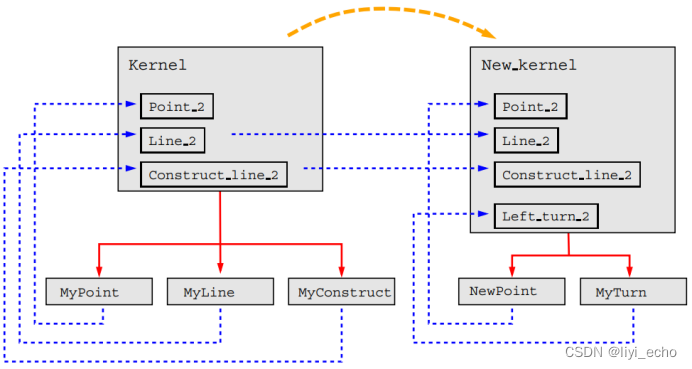
图2. 实例化问题。方框代表类，粗虚线箭头表示派生，实线箭头表示(模板)参数，
细点箭头必须被解读为typedef定义或继承的定义。
那要怎么告诉MyConstruct它现在应该将自己视为New_kernel的一部分?一个显然的解决方案是重新定义New_kernel中的Construct_line_2类型。在我们的示例中，这很好，因为它相当于仅仅只多了一个typedef。但考虑到一个真正的kernel里面会有数十种（几何对象）类型和数百种（对这些几何对象的）操作，必须重复所有这些定义将是非常繁琐的。注意，某些类可能无论如何都必须重新定义，例如一个类的更改可能会影响与该类交互的所有其他类。但通常这不是必要的，我们不希望这种重新定义成为一般需求。
幸运的是，找到了一条解决方法。若Kernel是用来构建自定义内核类的基础，在那个地方用Kernel实例化MyPoint<>, MyLine<>和MyConstruct<>是不明智的，因为那里可能不是这些类最终在其中结束的内核。我们更愿意推迟实例化，直到清楚实际的内核将是什么为止。这可以通过引入Kernel_base类作为“实例化引擎”来实现。实际的kernel类，如kernel和New_kernel都是从Kernel_base派生出来的，最后通过将自己注入基类开始实例化。

将一个类插入到它的基类中似乎有些奇怪，看起来像把一个类是插入到它自身。但是更仔细地观察它会发现，它的构造与前面的没有太大的不同，除了提供了额外的自由来确定何时实例化MyPoint等。这样通过派生(现在是从Kernel_base)创建New_kernel仍然很容易。为了能够以与Kernel相同的方式扩展New_kernel，我们再次推迟实例化。（下面New_kernel_base可以看作是系统预定义好的kernel，如Simple_cartesian、Cartesian等等。New_kernel可以看作是用户在，比如Cartesian基础上，自定义的kernel）

图3. 推迟实例化。方框代表类，粗虚线箭头表示派生，实线箭头表示(模板)参数，
细点箭头必须被解读为typedef定义或继承定义。
这样，通过在两个不同级别上使用内核作为模板参数，我们实现了易于扩展和适应性强的内核。内核中的几何对象类使用kernel作为模板参数，因此不同的几何对象有办法发现其他对象和操作的类型。因此，kernel中任何类型或操作的更改都会传播到相关的对象类中。而且kernel本身是从以kernel为模板的基类派生而来的，它确保（几何对象）类型和（对几何对象的）操作的实例化用的是派生类中的类型，而不是基类中的类型。

5 Functors

问题仍然存在：我们如何给与kernel交互的类和函数提供实际的函数。再次考虑上一节的例子：

这里我们关心的是kernel如何提供函数construct_line_2。实际上，有许多方法可以提供这样的函数，以确保kernel的适应性。然而，适应性并不是唯一需要考虑的问题。真正的kernel将包含许多结构（constructions）和谓词（predicates），它们大多数都很小，只有几行代码。但是这些函数将被调用大量的次数，在kernel上实现的算法中。它们之于几何学，犹如加法和乘法之于算术。因此，效率非常重要。
c风格的实现可能会在kernel中使用“函数指针”。

由于我们能修改指针（上例中的construct_line_2)，所以适应性是可以保证的。但是，对于小函数来说，调用函数指针带来相当大的性能损失（编译器碰到函数指针时，很多编译器优化会失效）。我们将在下面演示这种行为。用虚函数也有同样的问题。
因此，既然函数指针/虚函数开销这么大，那么将construct_line_2作为Kernel_base的普通成员函数如何?然后可以通过在派生类中重写该函数来调整它。实际上，我们所建议的只是更进一步，只是从编程语言中的具体函数转移到更抽象的级别。该解决方案受到标准c++库的启发，其中，许多算法都用所谓的“函数对象”（function objects）或“函数子”（functors）参数化。这个抽象背后的关键观察结果如下：某物是否是函数并不重要，只要它表现得像函数，就可以作为函数使用。那么函数的行为是什么?就是你可以通过使用括号和传递参数来调用它。
显然，任何函数都属于functor。此外定义了适当operator()的class类型的对象也可以是函数子。

这样，可以像使用函数一样使用Construct_line_2的任何实例。

至少有三个优点使这种抽象值得:效率、维护状态的能力以及更好的类型检查，这些都将在下面进行更详细的解释。尽管前两个优点可以通过使用内核类的普通成员函数来实现，但有一些原因表明函子更可取：
1.某些几何运算，写作functor后，可以与标准库中的算法(如sort等)一起使用。
2.函子彼此完全分离，可以独立维护它们的状态。
3.函子提供了一个统一的框架，使得数据类型和操作都只是kernel中的类型，且适应和修改它们的方式是一样的。
4.函子提供了更简单的调用语法，因为它独立于内核对象，而成员函数需要在每次调用中使用内核对象。
5.1 Efficiency of Functors
如果在编译时知道函子的完整类定义，则可以inline定义operator()。将函子作为模板实参传递给函数模板就像传递一段代码，可以按照编译器的喜好内联和优化。再次注意函子与传统函数指针或虚函数的对比。
为了支持这种说法，我们做了一个小测试:用冒泡排序对5000个偶数进行排序，从最坏情况的顺序开始。第一个函数使用内置操作符<比较数字，第二个函数用一个函数对象functor参数化，第三个函数用一个函数指针。使用优化良好的编译器，functor和“手工”版本在运行时上绝对没有区别，而函数指针会导致相当大的开销;见表1所示。

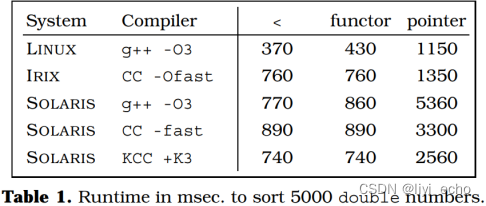
5.2 Functor with State
除了具有优化的潜力，函子也被证明比普通函数更灵活;class类型的函子还可以保存本地数据的状态。虽然也可以在成员函数或全局函数中使用静态变量实现“状态”，但这将禁止使用函数的多个实例，从而造成严格且难以检查的限制。且维护起来也很麻烦。
假设，为了进行基准测试，我们想要计算上面示例kernel中使用函子MyLess的次数。

每次调用这个函子，外部引用的计数器加1。另外，第8.3节中描述的投影特征需要一个状态来存储投影方向。
允许函数子使用本地数据给kernel增加了一点复杂性。显然，一个通用的算法不能关心函子是否携带局部状态。因此，算法不能实例化函子本身。如上例所示，具有局部状态的函数可能需要使用非默认构造函数。这里我们可以假设内核知道如何创建函子。因此，我们向内核添加访问成员函数（即下面的成员函数less_xy_2_object()），允许通用算法获取函子的对象。下面是上一节的kernel_base类。

construct_line_2_object和less_xy_2_object的实际实现分别依赖于MyConstruct和MyLess，并且可能与默认构造函数一样简单。（这里less_xy_2_object()是一个函数声明，该函数返回值类型为Less_xy_2）
5.3 Better Type Matching
函数的类型由其名字定义，而函子的类型则可以随心所欲地不同。这在模板参数匹配中是一个优势，因为在表示匹配类型集时有更大的自由度。

6 An Imperative Interface

习惯于命令式编程的人可能希望所有接口都是对几何类操作的成员函数和全局函数，而不是必须处理functor和kernel对象。由于我们设计的灵活性，我们可以很容易地在内核之上提供这样一个接口，且开销很小。
再次考虑确定一个点按字典序是否小于另一个点的操作。我们通过内核提供了类型Less_xy_2和成员函数Less_xy_2 object()来创建函子的实例。在kernel接口中将此操作作为全局函数提供也是很自然的。为了正确处理含状态的函子，kernel对象必须是这函子的参数。对于可以使用默认实参的函子，可以不提供kernel对象，因为默认kernel就能满足要求。

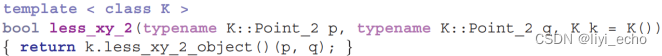
注意，如果省略了内核形参k，则无法从函数调用的实际形参中推导出类型k。因此，在本例中必须显式指定模板参数。（由K::Point_2不能推导出K吗？）

虽然这样的函数允许编写完全通用的代码，但人们可能仍然讨厌看起来多余的参数（在全局函数调用时）。在某些情况下，例如只使用一个kernel时，最好能够避免该参数。解决方案是为来自这个kernel的参数重载函数。

注意，这些专门化函数可以再次被模板化，例如通过一个数字类型，只要它们没有被内核类模板化。这样，专门化函数和具有内核模板形参的函数就可以和平共存，并且两种调用方式也可以同时使用。
比如想给几何类型添加一些功能。例如，如果内核支持从两个点构造一条线，那么MyLine类自然会有一个接受两个点参数的构造函数。

重要的是，MyLine不假设点类型，而是只使用K提供的操作。通过这种方式，几何类型保持了很好的分离，因为它们的关系(有时是密切的关系)被封装到适当的操作中。

7 A Function Toolbox

我们的kernel概念很好地将几何对象的表示与对这些对象的操作分离开来。但当实现一个特定的操作，如谓词Left_turn_2，对应的点类型Point_2的表示将不可避免地发挥作用。最后，使用对某些数字类型的算术运算来计算谓词。谓词和构造中需要的代数计算封装在内核体系结构的底层(图1)，即基于数字类型的函数工具箱，我们将在本节中描述它。
数字类型是指我们用来存储坐标和计算结果的数值类型。考虑到我们接受的输入数据是有理数，所以在有理数域内计算就足够了。对于某些运算，可能超越有理数演算（例如平方根）。但由于我们kernel的大部分算法只需要有理数的算术，所以这里暂时只关注有理数的运算。一个环(ring)支持“加”、“减”和“乘”。一个欧式环(Euclidean ring)除了支持ring的三个运算外，还支持整数的带余除法（这就能计算最大公约数了）。与之相比，域(field)还支持精确除法（不是整数除法）。
我们的内核中的许多操作都可以归结为行列式计算，例如，方向测试、圆内测试或段相交。例如，left-turn谓词通过计算由点坐标的差构建的2x2矩阵的行列式来实现。由于在其他几个谓词中也需要计算这样一个行列式，因此有必要将这一步分解为一个单独的函数，该函数由数字类型(这里FT为field类型)参数化，以保证灵活性:

该函数现在可以由需要计算2x2行列式的所有谓词和结构共享。这种代码重用是可取的，不仅因为它减少了维护开销，而且从健壮性的角度来看，它将潜在的问题隔离在少量的地方。这也增强了内核的适应性和可扩展性。

8 Adaptable Algorithms

在前面的小节中，我们演示了用于实现一个包含函子和（几何对象）类型的kernel的技术。在这里，我们将展示在算法的实现和自适应中，如何很好地使用这样的kernel。
8.1 Kernel as a Traits Class（略）
8.2 Adapting a Predicate
例如求凸包算法中需要用到left-turn，而left-turn谓词相当于求2x2-行列式的符号。如果直接通过双精度计算来实现这一点，由于舍入误差，不能保证结果是正确的。再怎么强调也不为过，这不仅仅是输出中的一些小错误的问题，例如，一些靠近凸包边界的点被错误地分类了，整个算法可能会崩溃，导致算法输出无用信息，甚至无休止地循环。
虽然有一个简单的解决方法，即使用精确的数字类型而不是double类型，但这通常需要付出相当大的性能损失。一种折中的解决方案是对普通浮点类型进行计算，并计算一个错误边界，从中可以推断结果是否正确（即知晓表达式的符号）。精确算术只在浮点计算无法给出正确结果的情况下使用，希望这种情况很少发生。所描述的技术称为floating point filtering[6, 16, 28]，根据计算误差界限的方式，可以将filter称为静态、半静态或动态。
现在，我们将描述如何调整内核以使用静态filter的left-turn谓词。假设，我们知道输入点的坐标是来自区间(-1,1)的double值。可以看出，在这种情况下，如果结果的绝对值超过下面的值，则可以从double计算中确定正确的符号：

将它插入我们的kernel是很简单的。

为凸包函数提供这样合适的核函数就可以保证得到正确的结果。
8.3 Projection Traits
正如在第5节中提到的，在traits类和内核类中使用函子的一个好处是可能将状态与函子关联起来。例如，可以利用这种灵活性将二维算法应用于三维共面点集。考虑一下在一个多面体上对一组点进行三角分割的问题。曲面的每个面都可以使用二维三角剖分算法分别进行三角剖分，并且可以编写一个核，它的二维部分在实际使用原始三维数据的时候，在所有函子中都做点向对应的平面上的投影。因此，谓词必须知道它们所操作的平面，这由函子的状态变量来维护。

9 Kernel Models

9.1 Coordinate Representation
我们区分两种坐标表示:笛卡尔坐标和齐次坐标。类模板Cartesian表示笛卡尔坐标，模板参数FT指示需要的是field类型数据。类模板Homogeneous表示齐次坐标，模板参数RT表示需要的是ring类型数据。齐次表示允许将除法分解为公分母，从而避免在计算中进行除法，这有时可以大大提高效率和鲁棒性。然而，笛卡尔表示避免了维护分母所需的额外时间和空间开销，因此对于某些应用程序也更有效。
9.2 Memory Allocation and Construction
优化的另一个方面是几何对象的内存布局。智能指针可以用引用计数句柄来加速对象的复制构造和赋值。运行时实验表明，对于大小超过某个阈值(大约4个word，取决于机器架构)的对象，该方案是有效的。为了易于选择，CGAL为每种表示提供了一个简单的、基于智能指针的版本。例如，对笛卡尔坐标系，有Simple_cartesian和Cartesian两个版本。
9.3 Filtered Models
基于精确计算范式的鲁棒几何算法方法需要对几何谓词进行精确的计算，即从几何计算中得到的决策必须是正确的。虽然这可以通过依赖精确的数字类型直接实现，但这并不是最有效的方法，而所谓的过滤器的思想被开发出来，以加快谓词的精确求值[6,16,28]。参见8.2节中的示例。
CGAL使用区间算法，通过数字类型Interval_nt[6]实现这种filter技术。此数字类型存储两个双精度值的间隔，该间隔的变化反映了浮点计算期间发生的舍入误差。此数字类型上的比较操作符具有这样一个属性:如果要比较的两个区间重叠，会抛一个c++异常。当这种情况发生时，这意味着过滤器不能使用它的近似计算来证明结果的准确性。然后，我们需要使用精确但较慢的数字类型来精确地计算谓词。由于这种失败通常很少发生，因此使用filter的总体性能与在区间内求值谓词的性能大致相同，这是相当快的。
CGAL提供了适配器Filter_predicate<>，这使得对给定的谓词使用filter技术很容易，还可以使用Filtered_kernel过滤kernel的所有谓词。下面是一个示例，演示如何创建filter的方向谓词。函子Cartesian::Orientation_2由一个field类型作为模板。这允许我们轻松构建经过filter的orientation谓词版本。我们只需将一个版本的谓词定义为区间数类型，另一个版本的谓词定义为高精度的数字类型，并使用这两个版本来定义filter后的谓词。

Filter_predicate<>有一个默认模板参数指定如何转换Point为Cartesian<interval_nt>::Point_2和Cartesian<leda_real>::Point_2，以便调用合适的版本.
9.4 Higher-dimensional Kernel（略）

10 Conclusions（略）

笔记
由于CGAL源代码大量运用了模板，所以读CGAL代码前需要先了解这些。
(1)偏特化：定义：针对template参数更进一步的条件限制所设计出来的一个特化版本。例如下代码：

(2)萃取(traits)，萃取的意义在于：普通的class可以自己定义value_type等，而c++内嵌类型数据却没有这些。traits后，就都有了。

testClass1和testClass2本来没有属性is_one，traits后就有了。（当然这两个类也可以自己定义出属性is_one，不需要萃取。）而重要的是最下面数字1没办法定义属性is_one。注意test_traits是空类，不会产生任何开销（就算有默认的构造，析构，最后也会由于类对象没有被使用而被编译器优化掉）。

参考文献：
1.https://inf.ethz.ch/~hoffmann/pub/hhkps-aegk-01a.pdf
2.https://www.cnblogs.com/grass-and-moon/p/10811110.html