五猴分桃问题详解

题目

有5只猴子在海边发现一堆桃子,决定第二天来平分.第二天清晨,第一只猴子最早来到,它左分右分分不开,就朝海里扔了一只,恰好可以分成5份,它拿上自己的一份走了.第2,3,4,5只猴子也遇到同样的问题,采用了同样的方法,都是扔掉一只后,恰好可以分成5份.问这堆桃子至少有多少只.据说没有一个同学能当场做出答案.怎么解？（据说这道问题是李政道教授提出来的）

一般性的解法

然后对于这道题思考，我能给出一个公式，会按如下设
设a为最后的结果,x为开始的结果
则： a = ((((((x-1)*5/4-1)*5/4)-1)*5/4-1)*5/4-1)*5/4
通过如上公式，就能实现算出最后的结果
然后注意结果的筛选

我们的思路是这样的，对每个X（整数）遍历进行通过如上公式的计算，然后算出a，当然 a能为带小数的形式，也能为整数形式，而整数形式的a即为所求。
然后这个算法的关键点是 ：
公式怎么实现
如何判断a是否为整数？
关于判断一个浮点数是否为整数，我在上一篇博客已经给出了解答

这里给出代码：

#include <iostream>
using namespace std;
int main(){
    for(int i=1;i<10000;i++){           //从1到10000作循环
        float res = i;
        for(int j=0;j<5;j++){
            res = (res-1)*4/5;
        }
        int temp =(int)res;
        if(temp==res){
            cout<<i<<" "<<res<<endl;
        }
    }
}

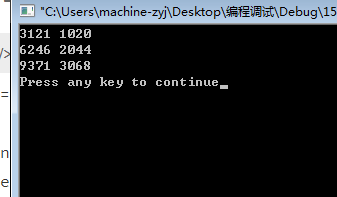
运行结果：

很明显，第一行数据就是我们想要的，3321是X 1020是a

巧解

巧解也是真的很巧，会满足这样一个条件，每次多出来一个，每次剩4/5，这样1为1/5的分子，这样就满足了

我们试试看给原来的桃子增添 4 个桃子（这点超级重要，至于为什么是4个，后面解析）
然后我们来看看效果；
原来多一个，现在加了4个，变成多5个，所有的桃子可以5等分了（假设每个猴子都不拿那多出来的一个）
然后第五个猴子过去了，这多出来的5个桃子还剩5*4/5 = 4个，加上多出来的一个又多出来5个了，所以又能5等分，后面的同理都能五等分
（听懂了吧？）
所以我们可以设桃子数目为x
则：
(x+4)*(五分之四的5次方) = 一个整数
所以1024/3125*（x+4）应该为一个整数，所以x最小为 3121

通过上面的一般方法得到的解也可以看到,X+4的值为3215的倍数

这就是简单方法了，希望大家能够喜欢！