三步PCA（主成分分析法）学习笔记

学习资料：Principal Component Analysis
in 3 Simple Steps

简介

PCA算法的主要目标是识别数据的模式，发现变量之间的相关性。当变量之间相关性较强时，PCA算法降维的作用变得非常有意义了。总结下来就是：找到高维数据的最大协方差的方向，在保留大多数信息的情况下将其投影到低维子空间。
整个PCA过程貌似及其简单，就是求协方差的特征值和特征向量，然后做数据转换。

PCA与LDA

LDA的的目标是找到不同类别之间的区别，其在模式分类问题中比较有用。

PCA和数据降维

我们能计算出数据的特征向量，每个特征向量都有其对应的特征值，当有些特征值明显大于另一部分时，我们通过PCA法在只损失少量信息的情况下将数据降维到子空间的做法是合理的。

PCA的技术路线

• 标准化数据
• 计算协方差矩阵的特征值和特征向量，或执行奇异向量分解（SVD）
• 按照特征值排序找到前K个最大特征值对应的特征向量，K是新的特征子空间的维度
• 按照所选K个特征向量组建投影矩阵W

• 通过矩阵W将原始数据集X投影到K位特征子空间Y

  其实PCA的本质就是对角化协方差矩阵。有必要解释下为什么将特征值按从大到小排序后再选。首先，要明白特征值表示的是什么？在线性代数里面我们求过无数次了，那么它具体有什么意义呢？对一个n∗n的对称矩阵进行分解，我们可以求出它的特征值和特征向量，就会产生n个n维的正交基，每个正交基会对应一个特征值。然后把矩阵投影到这n个基上，此时特征值的模就表示矩阵在该基的投影长度。特征值越大，说明矩阵（样本）在对应的特征向量上投影后的方差越大，样本点越离散，越容易区分，信息量也就越多。因此，特征值最大的对应的特征向量方向上所包含的信息量就越多，如果某几个特征值很小，那么就说明在该方向的信息量非常少，我们就可以删除小特征值对应方向的数据，只保留大特征值方向对应的数据，这样做以后数据量减小，但有用的信息量都保留下来了。PCA就是这个原理。

Iris数据集的准备

数据介绍

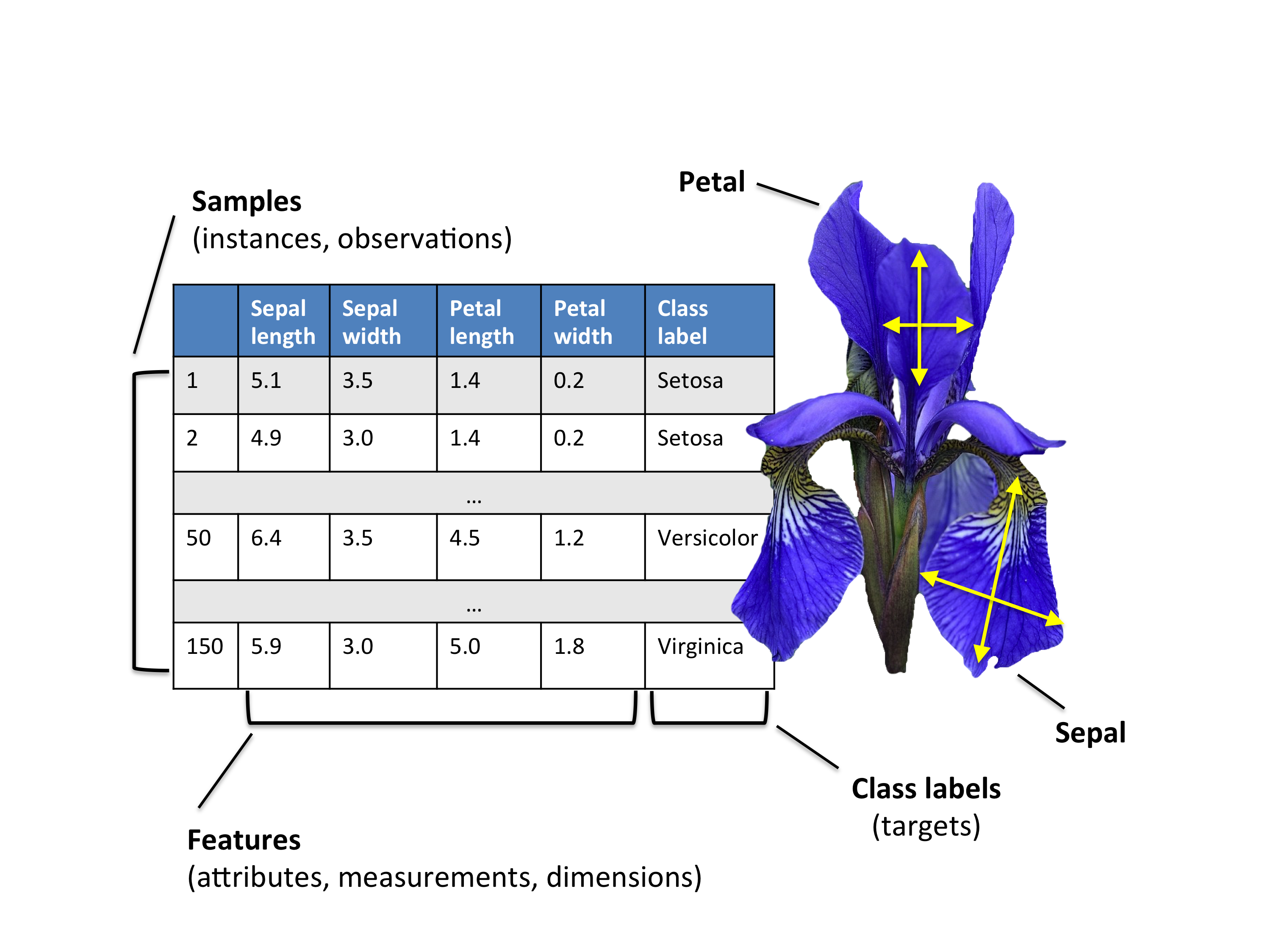
Iris数据集
数据集包含3种共150个鸢尾花图片
Iris-setosa (n=50)
Iris-versicolor (n=50)
Iris-virginica (n=50)

鸢尾花有四种特征 （cm）
1. 萼片长度
2. 萼片宽度
3. 花瓣长度
4. 花瓣宽度

加载数据集

利用pandas直接从UCI库加载数据集或从sklearn.datasets加载数据集
示例：http://www.cnblogs.com/Belter/p/8831216.html

数据标准化

根据原始特征的测算规模判断是否需要在使用PCA算法前对数据进行标准化，因为PCA会在保证轴向协方差最大的情况下产生相应的特征子空间，特比是在度量尺度不同的情况下，对数据进行标准化就变得格外重要。虽然Iris数据集中的特征都是以cm为单位，我们还是将数据转换为单位尺寸（均值为0，方差为1），这样处理能使很多机器学习算法有更好的表现。

from sklearn.preprocessing import StandardScaler
X_std = StandardScaler().fit_transform(X)

1-特征分解：计算特征值和特征向量

协方差矩阵的特征向量特征值代表了PCA的核心：
主成分的特征向量决定了新的特征空间的方向，特征值决定了它们的分量。

协方差矩阵

经典的PCA方法是通过协方差矩阵（d*d）的每一个元素表示两个向量之间的协方差，向量之间的协方差可以通过如下方法计算得到：

我们用一下公式概括计算