第一讲(周一)
一、基本概念
-
什么是信号?
在数字信号处理中,信号是用有限精度的数的序列来表示的,而用数字运算来实现。
信息的物理表现形式
信号处理: 对信号分类,交换,滤波,估计,识别等 -
什么是系统?
广义:系统是由拖杆相互依赖、相互作用的书屋组合而成的具有特定功能的整体
相对于信号:系统是能够完成对信号传输、处理、存储、运算与再现的集合体
系统是将信号进行处理或变换以达到人们要求的各类设备,系统可以使硬件的,也可以是软件编程实现的。 -
什么是信号维度?
根据信号的不同特点,可以表示成一维变量或多维变量的函数。例:语音信号可以表示为时间的函数,而静止的图像可以表示为两个空间变量的亮度函数,视频图像是三维信号
-
信号的分类常见的三种方式?
1、周期/非周期信号
2、确定/随机信号
3、能量/功率信号 -
按取值方式不同,信号分为哪三种?
1、连续时间信号
2、离散时间信号
3、数字信号 -
系统的分类
1、连续时间信号系统(模拟信号系统)
2、离散时间信号系统
3、数字信号系统 -
数字信号处理系统组成
系统分类:
①、连续/离散系统
②、按线性信号:线性/非线性系统
③、按时变性分:时不变系统,时变系统
模拟信号处理与数字信号处理
1、抽样
2、量化
3、数字信号处理器
4、D/A转换
5、输出 -
数字信号处理系统实现方法
软件、硬件、DSP
二、序列
-
什么是序列
离散的时间信号
由连续时间信号抽样获得。 -
序列的和、积、翻褶、累加
和:两个序列同序号的数值逐项相加而构成一个新的序列
积:同序号的数值逐项对应相乘而构成一个新的序列
翻褶:若序列x(n),则x(-n),是以n=0的纵轴为对称轴将序列x(n)加以翻褶
累加:对序列进行积分 -
序列的移位
将某一序列,一次向左/右移动m位而得到一个新序列 -
序列的差分
向前差分:将序列先向左移动然后与原序列相减
向后差分:将序列先向右移动然后与原序列相减 -
序列的卷积
z ( n ) = ∑ m = − ∞ ∞ x ( m ) y ( n − m ) z(n)=\sum_{m=-\infty}^\infty x(m)y(n-m) z(n)=∑m=−∞∞x(m)y(n−m)
第二讲
- 单位抽样(冲击)序列
δ
\delta
δ
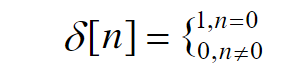
- 阶跃序列
u
(
n
)
u(n)
u(n)
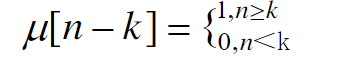
- 矩形序列
R
N
(
n
)
R_N(n)
RN(n)
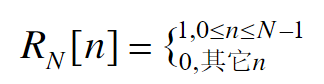
- 实指数序列
X
(
n
)
=
a
n
u
(
n
)
X(n) = a^nu(n)
X(n)=anu(n)
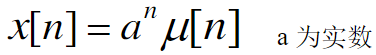
- 复指数数列
X
(
n
)
=
e
(
δ
+
j
ω
0
)
n
X(n) = e^{(\delta+j\omega _ 0)n}
X(n)=e(δ+jω0)n
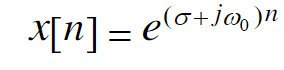
- 正弦序列
X
(
n
)
=
A
ξ
(
n
ω
0
+
ϕ
)
X(n) = A\xi(n\omega_0+\phi)
X(n)=Aξ(nω0+ϕ)
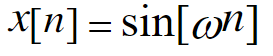
- 任意序列
X
(
n
)
=
∑
m
=
+
∞
∞
X
(
m
)
δ
(
n
−
m
)
X(n) =\sum_{m=+\infty}^\infty X(m)\delta(n-m)
X(n)=∑m=+∞∞X(m)δ(n−m)
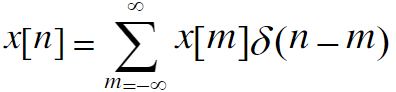
- 序列的周期性的判断与计算
满足 x ( n ) = x ( n + r N ) x(n) = x(n+rN) x(n)=x(n+rN),为周期序列
第三讲
- 系统的数学理解
运算符号:
T
[
x
(
n
)
]
T[x(n)]
T[x(n)]
2. 什么是线性系统?
若
y
1
(
n
)
=
T
[
x
1
(
n
)
]
和
y
2
(
n
)
=
T
[
x
2
(
n
)
]
y_1(n)=T[x_1(n)]和y_2(n)=T[x_2(n)]
y1(n)=T[x1(n)]和y2(n)=T[x2(n)]
满足
叠加原理:
T
[
a
1
x
1
(
n
)
+
a
2
x
2
(
n
)
]
=
a
1
y
1
(
n
)
+
a
2
y
2
(
n
)
T[a_1x_1(n)+a_2x_2(n)] = a_1y_1(n)+a_2y_2(n)
T[a1x1(n)+a2x2(n)]=a1y1(n)+a2y2(n)
或满足
可加性:
T
[
x
1
(
n
)
+
x
2
(
n
)
]
=
y
1
(
n
)
+
y
2
(
n
)
T[x_1(n)+x_2(n)] = y_1(n)+y_2(n)
T[x1(n)+x2(n)]=y1(n)+y2(n)
齐次性(比例性):
T
[
a
x
1
(
n
)
]
=
a
y
1
(
n
)
T[ax_1(n)] = ay_1(n)
T[ax1(n)]=ay1(n)
其中
a
,
a
1
,
a
2
a,a_1,a_2
a,a1,a2均为常数,此时此系统为线性系统
-
什么是时不变系统?
若系统响应与激励相加与系统的时刻无关则称为时不变系统
数学表达式:
对时不变系统若 T [ x ( n ) ] = y ( n ) T[x(n)]=y(n) T[x(n)]=y(n),
则 T [ x ( n − m ) ] = y ( n − m ) , m T[x(n-m)]=y(n-m),m T[x(n−m)]=y(n−m),m为任意常数 -
什么是单位抽样响应?
输入为单位抽样序列 δ ( n ) \delta(n) δ(n)时的系统输出 -
什么是卷积?
一个LSI系统可以用单位抽样响应h(n)来表征,任意输入的系统输出等于输入序列和该单位抽样响应h(n)的卷积和。
符号记做: y ( n ) = x ( n ) ∗ h ( n ) y(n)=x(n)*h(n) y(n)=x(n)∗h(n)
第四讲
-
卷积的具体计算
交换律: y ( n ) = x ( n ) ∗ h ( n ) = h ( n ) ∗ x ( n ) y(n)=x(n)*h(n)=h(n)*x(n) y(n)=x(n)∗h(n)=h(n)∗x(n)
结合律: x ( n ) ∗ h 1 ( n ) ∗ h 2 ( n ) = x ( n ) ∗ h 2 ( n ) ∗ h 1 ( n ) x(n)*h_1(n)*h_2(n)=x(n)*h_2(n)*h_1(n) x(n)∗h1(n)∗h2(n)=x(n)∗h2(n)∗h1(n), h ( n ) = h 1 ( n ) ∗ h 2 ( n ) , y ( n ) = x ( n ) ∗ h ( n ) h(n)=h_1(n)*h_2(n), y(n)=x(n)*h(n) h(n)=h1(n)∗h2(n),y(n)=x(n)∗h(n)
分配律: x ( n ) ∗ [ h 1 ( n ) + h 2 ( n ) ] = x ( n ) ∗ h 1 ( n ) + x ( n ) ∗ h 2 ( n ) x(n)*[h_1(n)+h_2(n)]=x(n)*h_1(n)+x(n)*h_2(n) x(n)∗[h1(n)+h2(n)]=x(n)∗h1(n)+x(n)∗h2(n) -
若 x ( n ) = x ( n ) R N ( n ) , h ( n ) = h ( n ) R M ( n ) 时 , 且 x ( n ) 在 x(n)=x(n)R_N(n),h(n)=h(n)R_M(n)时,且x(n)在 x(n)=x(n)RN(n),h(n)=h(n)RM(n)时,且x(n)在非零区间为 [ N 1 , N 2 ] [N_1,N_2] [N1,N2], h ( n ) h(n) h(n)在非零区间为 [ M 1 , M 2 ] [M_1,M_2] [M1,M2]系统输出 y ( n ) y(n) y(n)如何分段?
①当 M ≥ N M\ge N M≥N时则有分段为
n < 0 , 0 < n ≤ N − 1 , N ≤ n ≤ M − 1 , M ≤ n ≤ M − 1 , M ≤ n ≤ N + M − 2 , n ≤ N + M − 1 n<0,0<n\le N-1,N\le n \le M-1,M \le n \le M-1,M\le n \le N+M-2,n \le N+M-1 n<0,0<n≤N−1,N≤n≤M−1,M≤n≤M−1,M≤n≤N+M−2,n≤N+M−1②当 M ≤ N M\le N M≤N时则有分段为
n < 0 , 0 < n ≤ M − 1 , M ≤ n ≤ N − 1 , N ≤ n ≤ N + M − 2 , n ≥ N + M − 1 n<0,0<n\le M-1,M\le n \le N-1,N \le n \le N+M-2,n \ge N+M-1 n<0,0<n≤M−1,M≤n≤N−1,N≤n≤N+M−2,n≥N+M−1 -
有限长序列 x ( n ) x(n) x(n)长 N , h ( n ) N,h(n) N,h(n)长 M M M卷积和长度为多少?
设卷积和长度为 L L L: L = N + M − 1 L=N+M-1 L=N+M−1 -
LSI系统的基本概念
语义层面:LSI(Linear Shift Invariant)
实际含义:同时具有线性和移不变性的离散时间系统
第五讲
-
什么是因果系统?什么是特征方程?
因果系统:若系统中 n n n时刻的输出,只取决于 n n n时刻以及 n n n时刻以前的输入序列,而与 n n n时刻以后的输入无关,则 h ( n ) = 0 , n < 0 h(n)=0,n<0 h(n)=0,n<0
特征方程:研究相应的数学对象而引入的一些等式,它因数学对象不同而不同。 -
什么是常系数线性差分方程?
描述时域离散系统的输入与输出关系
由未知输出序列项与输入序列项构成的方程。 -
差分方程的经典解法,递推解法,变换域解法
1、经典解法:
①、列齐次方程
②、求特征方程
③、求特征根
④、代入初始值
⑤、列出 y ( n ) y(n) y(n)
与连续系统的微分方程经典解类似,差分方程的解由齐次解yh(k)和特解yp(k)两部分组成,齐次解是对应齐次差分方程的解,由特征根可以设定齐次解的函数形式,特解的函数形式与激励的函数形式有关。2、递推解法:
①、令 r ( n ) = δ ( n ) r(n)=\delta(n) r(n)=δ(n)
②、由 n < 0 求 r ( n ) = 0 n<0 求r(n)=0 n<0求r(n)=0
③、递推 h ( 0 ) h ( n ) h(0)~h(n) h(0) h(n)
差分方程本质上是递推的代数方程,若已知初始条件和激励,利用迭代法可求得其数值解。3、变换域解法:利用Z变换进行求解
-
将差分方程 y ( n ) − a y ( n − 1 ) = x ( n ) y(n)-ay(n-1)=x(n) y(n)−ay(n−1)=x(n)表示成结构框图
四、抽样(周二)
-
什么是抽样?什么是抽样信号?
抽样:把模拟信号以其信号带宽2倍以上的频率提取样值,变为在时间轴上离散的抽样信号的过程。利用抽样脉冲序列 p ( t ) p(t) p(t)从边续信号 f ( t ) f(t) f(t)中“抽取”一系列的离散样值的过程。抽样信号:经抽取后的一系列的离散信号,一般称为抽样函数或Sa(t)函数,是指sint与t之比构成的函数。
-
什么是抽样脉冲序列?
用于对模拟信号进行抽样的序列称为抽样脉冲,可以采用不同的抽样脉冲进行抽样,有矩形脉冲抽样(自然抽样)和冲击抽样(理想抽样) -
什么是理想抽样?什么是理想抽样频谱?
冲击抽样(理想抽样)
理想抽样频谱: F s ( w ) = ∑ n = − ∞ ∞ F ( w − n w s ) F_s(w)=\sum_{n=-\infty}^\infty F(w-nw_s) Fs(w)=∑n=−∞∞F(w−nws) -
什么是抽样定理?什么是频域抽样定理?
抽样定理:通信理论中的一个重要定理,是模拟信号数字化的理论依据,包括时域抽样定理和频域抽样定理两部分。
抽样后能够不失真地还原出原信号,则抽样频率必须大于两倍信号谱的最高频率。 -
什么是频域抽样?
在时域对信号进行采样,等效为在频域对信号频谱进行周期延拓。在频域对频谱进行采样,等效为在时域对信号进行周期延拓。 -
恢复原始信号的条件是什么?
1、待取样信号必须是时限信号
2、取样频率需要大于等于原信号的2倍 -
什么是频谱混叠?
频谱混叠是指取样信号被还原成连续信号时产生彼此交叠而失真的现象 -
正弦信号抽样的要求
对正弦信号,需满足 f s > 2 f 0 f_s>2f_0 fs>2f0
第一讲(周三)
- Z变换及其收敛域是什么?
Z变换定义: X ( z ) = Z T [ x ( n ) ] = ∑ n = − ∞ ∞ x ( n ) z − n X(z)=ZT[x(n)]=\sum_{n=-\infty}^\infty x(n)z^{-n} X(z)=ZT[x(n)]=∑n=−∞∞x(n)z−n
对于任意给定序列x(n),使其z变换X(z)收敛的所有z值的集合称为X(z)的收敛域。 - ①什么是有限长序列?
x ( n ) = x ( n ) , n 1 ≤ n ≤ n 2 x(n)=x(n) , n_1\le n \le n_2 x(n)=x(n),n1≤n≤n2
x ( n ) = 0 , 其 他 n x(n)=0,其他n x(n)=0,其他n
②什么是右边序列?
x ( n ) = x ( n ) , n ≥ n 1 x(n)=x(n) , n\ge n_1 x(n)=x(n),n≥n1
x ( n ) = 0 , n < n 1 x(n)=0,n<n_1 x(n)=0,n<n1
③什么是左边序列?
x ( n ) = x ( n ) , n ≤ n 2 x(n)=x(n) , n\le n_2 x(n)=x(n),n≤n2
x ( n ) = 0 , n > n 2 x(n)=0,n>n_2 x(n)=0,n>n2
④什么是双边序列?
n n n为任意值时皆有值
第二讲
-
什么是留数?
解析函数沿着某一圆环域内包围某一孤立奇点的任一正向简单闭曲线的积分值除以2πi。留数数值上等于解析函数的洛朗展开式中负一次幂项的系数。 -
什么是留数定理?
用来计算解析函数沿着闭曲线的路径积分的一个有力的工具,也可以用来计算实函数的积分。它是柯西积分定理和柯西积分公式的推广。 -
IZT是什么?
IZT: x ( n ) = I Z T [ x ( n ) ] = ∑ n = − ∞ ∞ x ( n ) z − n , R x − < ∣ z ∣ < R x + x(n)=IZT[x(n)]=\sum_{n=-\infty}^\infty x(n)z^{-n},R_{x_-}<|z|<R_{x_+} x(n)=IZT[x(n)]=∑n=−∞∞x(n)z−n,Rx−<∣z∣<Rx+ -
常见的ZT列表
ZT: X ( n ) = Z T [ x ( n ) ] = ∑ n = − ∞ ∞ x ( n ) z − n , R x − < ∣ z ∣ < R x + X(n)=ZT[x(n)]=\sum_{n=-\infty}^\infty x(n)z^{-n},R_{x_-}<|z|<R_{x_+} X(n)=ZT[x(n)]=∑n=−∞∞x(n)z−n,Rx−<∣z∣<Rx+
第三讲
-
ZT的八大性质是什么?
1、线性2、序列的移位: 若 Z T [ x ( n ) ] = X ( z ) , R x − < ∣ z ∣ < R x + 则 Z T [ x ( n − m ) ] = z − m X ( z ) , m 为 任 意 整 数 , R x − < ∣ z ∣ < R x + 若ZT[x(n)]=X(z),R_{x^-}<|z|<R_{x^+} 则ZT[x(n-m)]=z^{-m}X(z),m为任意整数,R_{x^-}<|z|<R_{x^+} 若ZT[x(n)]=X(z),Rx−<∣z∣<Rx+则ZT[x(n−m)]=z−mX(z),m为任意整数,Rx−<∣z∣<Rx+
3、与指数序列相乘:若 Z T [ x ( n ) ] = X ( z ) , R x − < ∣ z ∣ < R x + 则 Z T [ a n x ( n ) ] = X ( z a ) , a 为 任 意 整 数 , ∣ a ∣ R x − < ∣ z ∣ < ∣ a ∣ R x + ZT[x(n)]=X(z),R_{x^-}<|z|<R_{x^+} 则ZT[a^nx(n)]=X(\frac {z}{a}),a为任意整数,|a|R_{x^-}<|z|<|a|R_{x^+} ZT[x(n)]=X(z),Rx−<∣z∣<Rx+则ZT[anx(n)]=X(az),a为任意整数,∣a∣Rx−<∣z∣<∣a∣Rx+
4、序列线性加权:若 Z T [ x ( n ) ] = X ( z ) , R x − < ∣ z ∣ < R x + 则 Z T [ n x ( n ) ] = − z d d z X ( z ) , R x − < ∣ z ∣ < R x + ZT[x(n)]=X(z),R_{x^-}<|z|<R_{x^+} 则ZT[nx(n)]=-z\frac {d}{dz}X(z),R_{x^-}<|z|<R_{x^+} ZT[x(n)]=X(z),Rx−<∣z∣<Rx+则ZT[nx(n)]=−zdzdX(z),Rx−<∣z∣<Rx+
5、共轭序列:若 Z T [ x ( n ) ] = X ( z ) , R x − < ∣ z ∣ < R x + 则 Z T [ n ∗ ( n ) ] = X ∗ ( z ∗ ) , R x − < ∣ z ∣ < R x + ZT[x(n)]=X(z),R_{x^-}<|z|<R_{x^+} 则ZT[n*(n)]=X*(z*),R_{x^-}<|z|<R_{x^+} ZT[x(n)]=X(z),Rx−<∣z∣<Rx+则ZT[n∗(n)]=X∗(z∗),Rx−<∣z∣<Rx+
6、翻褶序列:若 Z T [ x ( n ) ] = X ( z ) , R x − < ∣ z ∣ < R x + 则 Z T [ x ( − n ) ] = X ( 1 z ) , R x − < ∣ z ∣ < R x + ZT[x(n)]=X(z),R_{x^-}<|z|<R_{x^+} 则ZT[x(-n)]=X(\frac{1}{z}),R_{x^-}<|z|<R_{x^+} ZT[x(n)]=X(z),Rx−<∣z∣<Rx+则ZT[x(−n)]=X(z1),Rx−<∣z∣<Rx+
7、初值定理:对于因果序列 x ( n ) x(n) x(n)有 lim n → ∞ X ( z ) = x ( 0 ) \lim_{n \to \infty}X(z)=x(0) limn→∞X(z)=x(0)
8、终值定理: Z T [ x ( n ) ] = X ( z ) ZT[x(n)]=X(z) ZT[x(n)]=X(z)的极点处于单位圆以内(单位圆上最多 z = 1 z=1 z=1处可有一阶极点), lim n → ∞ x ( n ) = lim z → 1 [ ( z − 1 ) X ( z ) ] \lim_{n\to\infty}x(n)=\lim_{z\to1}[(z-1)X(z)] limn→∞x(n)=limz→1[(z−1)X(z)]
第四讲
- ZT与FT、LT的关系是什么?
第五讲
- 列出差分方程Z域解法的具体步骤
1)、对差分方程进行单边z变换(移位性质)
2)、由z变换方程求出相应Y(z)
3)、求Y(z)的反变换,得到y(n)
第六讲
-
什么是系统函数?
在LSI系统中系统函数为单位抽样响应h(n)的z变换 -
什么是频率响应?
单位圆上的系统函数单位抽样响应h(n)的傅里叶变换
CH3(周四)
-
概述:写出四种信号及其描述方法
1)、Laplace变换: X ( s ) = ∫ 0 ∞ x ( t ) e − s t d t , x ( t ) = 1 2 π j ∫ δ − j ∞ δ + j ∞ X ( s ) e s t d s X(s)=\int_0^\infty x(t)e^{-st}dt,x(t)=\frac{1}{2\pi j}\int_{\delta -j \infty}^{\delta +j \infty}X(s)e^{st}ds X(s)=∫0∞x(t)e−stdt,x(t)=2πj1∫δ−j∞δ+j∞X(s)estds2)、 z z z变换 X ( z ) = ∑ n = − ∞ ∞ x ( n ) z − n , x ( n ) = ∮ c X ( z ) z ( n − 1 ) d z , c ∈ ( R 1 , R 2 ) X(z)=\sum_{n=-\infty}^\infty x(n)z^{-n},x(n)=\oint_cX(z)z^{(n-1)}dz,c\in(R_1,R_2) X(z)=∑n=−∞∞x(n)z−n,x(n)=∮cX(z)z(n−1)dz,c∈(R1,R2)
3)、连续时间傅里叶变换 X ( j Ω ) = ∫ − ∞ + ∞ x ( t ) e − j Ω t , x ( t ) = 1 2 π ∫ − ∞ + ∞ X ( j Ω ) e − j Ω t d Ω X(j\Omega)=\int_{-\infty}^{+\infty}x(t)e^{-j\Omega t },x(t)=\frac{1}{2\pi}\int_{-\infty}^{+\infty}X(j\Omega)e^{-j\Omega t }d\Omega X(jΩ)=∫−∞+∞x(t)e−jΩt,x(t)=2π1∫−∞+∞X(jΩ)e−jΩtdΩ
4)、离散时间的傅里叶变换 X ( e j ω ) = ∑ n = − ∞ ∞ x ( n ) e − j ω n , x ( n ) = 1 2 π ∫ − π π X ( e j ω ) e j ω n d ω X(e^{j\omega})=\sum_{n=-\infty}^{\infty}x(n)e^{-j\omega n},x(n)=\frac{1}{2\pi}\int_{-\pi}^{\pi}X(e^{j\omega})e^{j\omega n}d\omega X(ejω)=∑n=−∞∞x(n)e−jωn,x(n)=2π1∫−ππX(ejω)ejωndω
-
DFS四个性质是什么?
1、线性
2、序列的移位
3、调制特性
4、周期卷积和 -
什么是DFT? W N = W_N = WN=?
①、x(n)的N点DFT是
②、x(n)的z变换在单位圆上的N点等间隔抽样
③、x(n)的DTFT在区间[0,2π]上的N点等间隔抽样。
W N = e − j 2 π N W_N =e^{-j\frac{2\pi}{N}} WN=e−jN2π -
DFT的六个性质
1、线性
2、序列的圆周移位:有限长序列的圆周移位导致频谱线性相移,而对频谱幅度无影响,时域序列的调制等效于频域的圆周移位
3、圆周卷积和
4、共轭对称性
5、复共轭序列
6、DFT形式下的Parseval定理 -
什么是时域周期卷积特性?频域卷积特性?
时域卷积特性:两个时间函数卷积的频谱等于各个时间函数频谱的乘积
频域卷积特性:两个时间函数频谱的卷积等效于各个时间函数的乘积(乘以系数 1 2 π \frac{1}{2\pi} 2π1) -
什么是圆周移位?定理?
一个长度为N的有限长序列 x ( n ) x(n) x(n)的圆周移位定义为: y ( n ) = x ( ( n + m ) ) N R N ( n ) y(n)=x((n+m))_NR_N(n) y(n)=x((n+m))NRN(n)

-
什么是循环卷积?定理?
循环卷积可以通过循环卷积定理转化为各自的DFT的乘积循环卷积是使用DFT(FFT)计算线性卷积时的衍生品。首先连续时间没有循环卷积概念。离散时间时,不妨假设x(n)为L点信号, 仅在0L-1有非零值;h(n)为M点信号,仅在0M-1有非零值。以x(n)为输入信号通过以h(n)为单位冲激响应的线性时不变系统得到输出 y(n) = x(n) * h(n),线性卷积,直接计算的复杂度为 O(LM)。
-
什么是离散相关函数
连续函数的相关函数:
设序列 x ( n ) x(n) x(n)和 y ( n ) y(n) y(n)为能量信号,其能量分别为 E x E_x Ex和 E y E_y Ey,
令 r x y ( δ ) = ∑ n = − ∞ + ∞ x ( n ) y ( n − δ ) , p x y ( δ ) = r x y ( δ ) E x E y r_xy(\delta)=\sum_{n=-\infty}^{+\infty}x(n)y(n-\delta),p_xy(\delta)=\frac{r_xy(\delta)}{\sqrt{E_xE_y}} rxy(δ)=∑n=−∞+∞x(n)y(n−δ),pxy(δ)=ExEyrxy(δ)
(1)称 r x y ( δ ) r_xy(\delta) rxy(δ)为序列 x ( n ) x(n) x(n)和 y ( n ) y(n) y(n)的互相关函数
(2)称 r x x ( δ ) 、 p x x ( δ ) r_xx(\delta)、p_xx(\delta) rxx(δ)、pxx(δ)为序列x(n)的自相关函数
离散函数的相关函数:
将时移量 δ \delta δ离散化,则得到相关函数 r x y ( δ ) r_xy(\delta) rxy(δ)的离散值:
r x y ( m ) = ∑ n = − ∞ + ∞ x ( n ) y ( n − m ) , m = 0 , ± 1 , ± 2 ⋅ ⋅ ⋅ ⋅ ⋅ r_xy(m)=\sum_{n=-\infty}^{+\infty}x(n)y(n-m),m=0,±1,±2····· rxy(m)=∑n=−∞+∞x(n)y(n−m),m=0,±1,±2⋅⋅⋅⋅⋅
称 r x y ( m ) r_xy(m) rxy(m)为序列 x ( n ) 和 y ( n ) x(n)和y(n) x(n)和y(n)的离散互相关函数。 -
DFT与ZT关系是什么?
单位圆上的等间隔采样点处的ZT等于该有限长序列的DFT。
CH4(周五)
-
描述基本FFT的原理
利用DFT系数的特性,合并DFT运算中的某些项,把长序列DFT → \to →短序列DFT,从而减少其运算量
FFT算法分类:
时间抽选法:DIT
频率抽选法:DIF -
4.1
倒位序列
00000
10000
01000
11000
00100
10100
01100
11100
00010
10010
01010
11010
00110
10110
01110
11110
00001
10001
01001
11001
00101
10101
01101
11101
00011
10011
01011
11011
00111
10111
01111
11111 -
4.2

-
4.3

-
时间抽选FFT有那些特点?P99
(1)、当 x ( n ) x(n) x(n)长为 N = 2 M N=2^M N=2M时,要进行 M M M次奇偶分解,分 M M M级计算
(2)、设L表示级数,L是正整数,它可以是1,2,···,M中的任意一个值。时间抽选奇偶分解FFT算法,其输入序列x(n)为倒位序,输出序列X(k)为自然顺序
(3)、可以“即位运算”指当把数据存入存储器之后,每一级运算的结果都存入相应的输入存储器中,知道计算出最终结果。
(4)、每一级包括N/2个基本碟形计算
(5)、第L级运算包括N/ 2 L 2^L 2L个群之间的间隔为 2 L 2^L 2L,L为1,2,···,M中的任意一个值
(6)、同一级中各个群的乘数W分布相同,每级共有 2 L − 1 2^{L-1} 2L−1个乘数
(7)、每一个群中,W分布自上而下的规律为 W N N 2 L W_N^{\frac{N}{2^L}} WN2LN的从零开始的正整数次幂
(8)、
每一个蝶形计算关系:
A L ( p ) = A L − 1 ( p ) + W N r A L − 1 ( p − 2 L − 1 ) A_L(p)=A_{L-1}(p)+W_N^rA_{L-1}(p-2^{L-1}) AL(p)=AL−1(p)+WNrAL−1(p−2L−1)
A L ( p + 2 L − 1 ) = A L − 1 ( p ) + W N r A L − 1 ( p − 2 L − 1 ) A_L(p+2^{L-1})=A_{L-1}(p)+W_N^rA_{L-1}(p-2^{L-1}) AL(p+2L−1)=AL−1(p)+WNrAL−1(p−2L−1)
蝶形计算输入序列间隔为 2 L − 1 2^{L-1} 2L−1 -
简述IDFT算法P108
将DFT中的每一个乘数 W N n k W_N^{nk} WNnk改成W_N^{-nk},并且将最后的结果乘以1/N,那么时间抽选奇偶分解FFT算法与频率抽选奇偶分解FFT算法就可以直接用于IDFT计算。
CH5(周六)
-
描述数字滤波的工作原理P125
x 0 ( t ) → H 1 ( s ) → x ( t ) → 抽 样 → 量 化 → x ( n ) → H ( z ) → y ( n ) → D / A 变 换 器 → y s ( t ) → H 2 ( s ) → y ( t ) x_0(t)\to H_1(s)\to x(t)\to抽样\to量化\to x(n)\to H(z)\to y(n)\to D/A变换器\to y_s(t)\to H_2(s)\to y(t) x0(t)→H1(s)→x(t)→抽样→量化→x(n)→H(z)→y(n)→D/A变换器→ys(t)→H2(s)→y(t) -
根据h(n)特性数字滤波分为哪几类?P128
(1) 无限冲激响应(IIR)数字滤波器
(2) 有限冲激响应(FIR)数字滤波器 -
描述IIR的系统函数,差分方程及结构形式P129
系统函数: H ( z ) = ∑ j = 0 N b j z − j 1 − ∑ i = 1 N a i z − i H(z)=\frac{\sum_{j=0}^{N}b_jz^{-j}}{1-\sum_{i=1}^Na_iz^{-i}} H(z)=1−∑i=1Naiz−i∑j=0Nbjz−j
差分方程: y ( n ) = ∑ i = 1 N a i y ( n − i ) + ∑ j = 0 N b j x ( n − j ) , a i 不 完 全 为 零 y(n)=\sum_{i=1}^{N}a_iy(n-i)+\sum_{j=0}^{N}b_jx(n-j),a_i不完全为零 y(n)=∑i=1Naiy(n−i)+∑j=0Nbjx(n−j),ai不完全为零 -
描述FIR的系统函数,差分方程及结构形式P136
系统函数: H ( z ) = ∑ n = 0 N − 1 h ( n ) z − n H(z)=\sum_{n=0}^{N-1}h(n)z^{-n} H(z)=∑n=0N−1h(n)z−n
差分方程: y ( n ) = ∑ m = 0 N − 1 h ( m ) x ( n − m ) y(n)=\sum_{m=0}^{N-1}h(m)x(n-m) y(n)=∑m=0N−1h(m)x(n−m) -
5.1P141
不对,在输入端加入抗混叠滤波器仅能去除一部分的输入干扰,加入数字部分不仅可以更加方便的补偿部分缺失信号,将信号更为细致的处理,还更加利于信号的远距离传输。 -
5.2
不对,在输出端接入低通滤波器目的是便于将D/A变换器输出的模拟量良好的恢复为连续信号进行输出,故输出的低通滤波器并不是单独的滤波作用。






















 4389
4389











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








