一.因子分析概述
昨天介绍了主成分分析(PCA),PCA能起到很好的降维作用,但要对多个主成分进行符合实际意义的解释比较困难,在昨天的例子中,只有前两个主成分F1和F2能得到较好的解释。而因子分析可以看作是对PCA的一种推广和发展,通过因子旋转可以使变量在降维之后能得到更好的解释。因子分析和PCA的不同还在于因子分析需要构造一个因子模型,原始变量是因子的线性组合。
因子模型用向量可表示为:x=μ+Af+ε
其中f=(f1,f2,..fm)'为公共因子向量,ε=(ε1,ε2,...εp)'为特殊因子向量,A为因子载荷矩阵
并假定E(f)=0, E(ε)=0, V(f)=I, Cov(f,ε)=0
由以上可以看出公共因子彼此不相关并且有单位方差,特殊因子与公共因子也不相关。
x的协方差可以分解为AA'+D
因子载荷矩阵A的一些性质:
1.A的元素aij就是xi与fi之间的相关系数
2.A的行元素平方和称为共同度(共性方差),反映了公共因子f1,f2,..fm对xi的影响。
3.A的列元素平方和称为公共因子fi对x1,x2,..xp的方差贡献度,反映了公共因子fi对x1,x2...xp的影响
因子旋转:
如果载荷矩阵A的所有元素都接近0或±1,则模型的公共因子就易于解释,这样就可以将原始变量x1,x2,..xp分成m各部分,第一部分对应第一个公共因子f ,第m个部分对应第m个公共因子fm。
对公共因子作正交旋转相当于对载荷矩阵A作一正交变换,右乘正交矩阵T,使A*=AT。从几何上看,就是在m维空间对原因子轴作旋转。由于A*A*'=ATT'A'=AA',故因子旋转不改变共性方差和残差矩阵。而正交矩阵T的选取不同导致正交矩阵有好几种方法,最普遍的要数最大方差旋转法(Varimax),它是使旋转后的矩阵A*所有m个列元素平方的相对方差之和达到最大。
二.SAS实现
procfactor data=tmp1.innovation n=3 r=v out=a1; #输出3个因子,r=v代表因子旋转的方法是varimax
run;
data a2;
set a1;
F=(Factor1*4.467+Factor*4.31+Factor3*2.60)/14; #对三个因子求加权平均,权重是各因子的方差贡献率
keep region F Factor1 Factor2 Factor3;
run;
proc print data=a2;
run;
三.SAS输出结果及解释

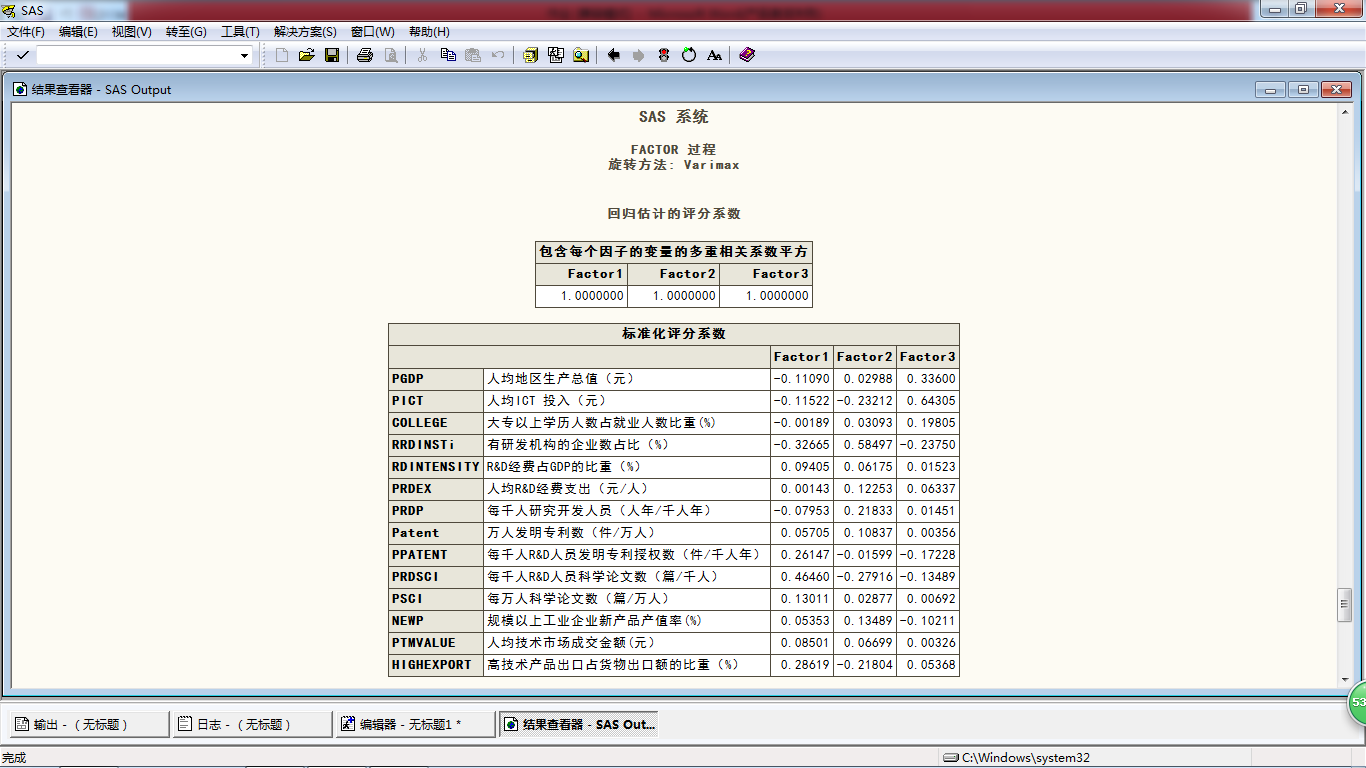
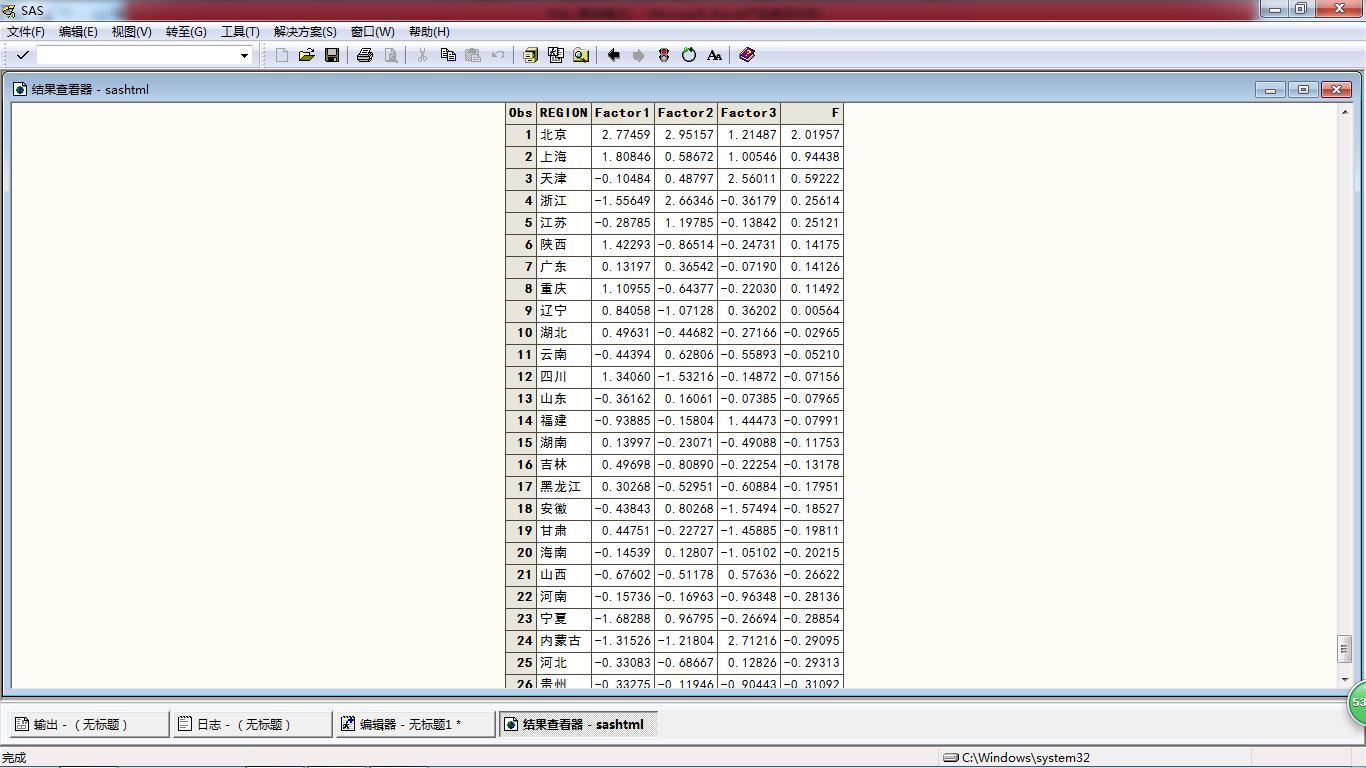








 本文介绍了因子分析的基本原理及其与主成分分析的区别,并详细解释了因子模型的构成要素,如因子载荷矩阵、共同度等。此外,还提供了使用SAS软件进行因子分析的具体步骤及结果解读。
本文介绍了因子分析的基本原理及其与主成分分析的区别,并详细解释了因子模型的构成要素,如因子载荷矩阵、共同度等。此外,还提供了使用SAS软件进行因子分析的具体步骤及结果解读。
















 2524
2524

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








