申明： 仅个人小记
一、相似矩阵
P − 1 A P = B {P}^{-1}AP=B P−1AP=B
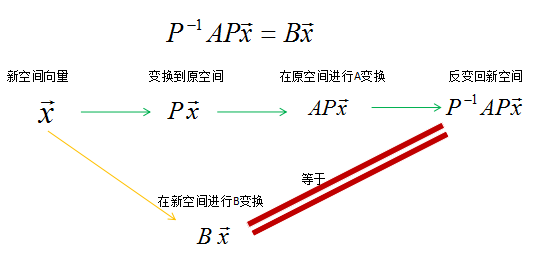
P − 1 A P x ⃗ = B x ⃗ {P}^{-1}AP\vec{x}=B\vec{x} P−1APx=Bx
x ⃗ \vec{x} x是新空间的一个向量， P x ⃗ P\vec{x} Px表示将新空间向量 x ⃗ \vec{x} x变换为原空间向量， A P x ⃗ AP\vec{x} APx是在原空间下做A变换, P − 1 A P x ⃗ {P}^{-1}AP\vec{x} P−1APx是将变换结果反变回新空间， B x ⃗ B\vec{x} Bx是在新空间下对向量 x ⃗ \vec{x} x做B变换
对上式进行变形，得 A = P B P − 1 A=PB{P}^{-1} A=PBP−1
A
y
⃗
=
P
B
P
−
1
y
⃗
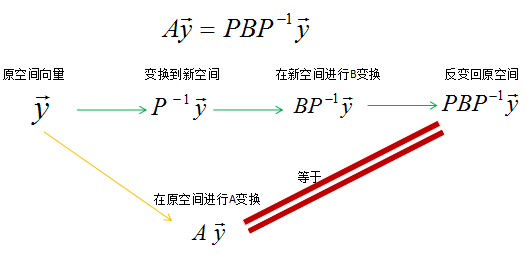
A\vec{y}=PB{P}^{-1}\vec{y}
Ay=PBP−1y
此时，
y
⃗
\vec{y}
y是原空间的一个向量，
P
−
1
y
⃗
{P}^{-1}\vec{y}
P−1y是将原空间向量
y
⃗
\vec{y}
y变换到新空间，
B
P
−
1
y
⃗
B{P}^{-1}\vec{y}
BP−1y则是在新空间中对向量
P
−
1
y
⃗
{P}^{-1}\vec{y}
P−1y做B变换，
P
B
P
−
1
y
⃗
PB{P}^{-1}\vec{y}
PBP−1y便是将变换结果
P
−
1
y
⃗
{P}^{-1}\vec{y}
P−1y变换到原空间。
####二、过渡矩阵
R
3
{R}^{3}
R3空间的一个基
A
=
(
α
⃗
1
,
α
⃗
2
,
α
⃗
3
)
A=(\vec \alpha _1,\vec \alpha_2,\vec \alpha _3)
A=(α1,α2,α3)，在取一个新基
B
=
(
β
⃗
1
,
β
⃗
2
,
β
⃗
3
)
B=(\vec \beta_1,\vec \beta_2,\vec\beta_3)
B=(β1,β2,β3)，把矩阵
P
=
A
−
1
B
P={A}^{-1}B
P=A−1B称为旧基A到新基B的过渡矩阵。
为什么这样称呼，看下式：
B
=
A
P
B=AP
B=AP
即对基A做变换P就可以得到基B。(为什么这样，我暂时不清楚，只当是选出一种作为规定吧)。
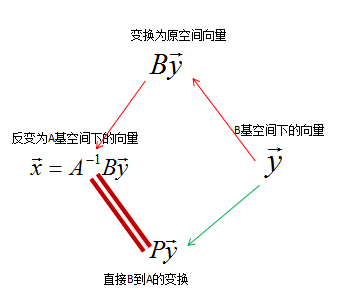
具体用处， x ⃗ = A − 1 B y ⃗ , 其 中 x ⃗ 是 基 A 下 的 坐 标 ， y ⃗ 是 基 B 下 的 坐 标 \vec{x}={A}^{-1}B\vec{y}, 其中\vec{x}是基A下的坐标，\vec{y} 是基B下的坐标 x=A−1By,其中x是基A下的坐标，y是基B下的坐标
B y ⃗ B\vec{y} By是将B基下的向量 y ⃗ \vec y y变换到原空间， A − 1 B y ⃗ {A}^{-1}B\vec{y} A−1By表示将原空间的向量 B y ⃗ B\vec{y} By变换到A基下的向量。
扫一扫
4248
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
