最短路径和距离及可视化——matlab

文章目录

一、前言

二、最短路线

2.1 教程

2.1.1 sparse创建稀疏矩阵

2.1.2 有向图最短路径（1）

2.1.3 有向图最短路径（2）

2.1.4 无向图最短路径（1）

2.1.5无向图最短路径（2）

---

一、前言

动态规划是求解某类问题的一种方法，是考察问题的一种途径，而不是一种特殊算法（如线性规划是一种算法）。因而，它不象线性规划那样有一个标准的数学表达式和明确定义的一组规则，而必须对具体问题进行具体分析处理。因此，在学习时，除了要对基本概念和方法正确理解外，应以丰富的想象力去建立模型，用创造性的技巧去求解。

二、最短路线

2.1 教程

2.1.1 sparse创建稀疏矩阵

比如我们有这样的无向图：

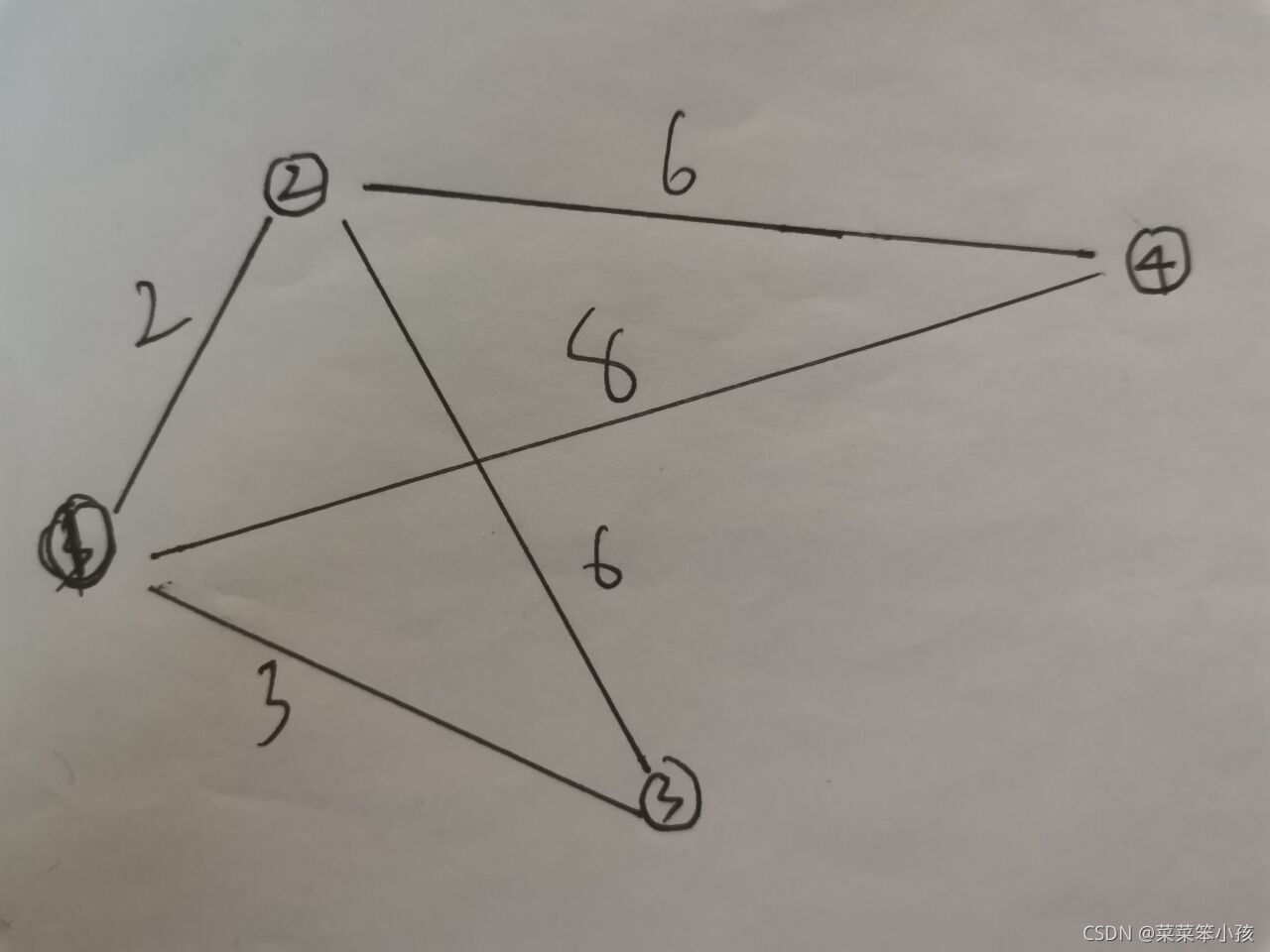
 代码：

%w(起点,终点)=权重值

clear all
clc
w=zeros(4);
w(1,2)=2;w(1,3)=3;w(1,4)=8; 
w(2,3)=6;w(2,4)=6;
G=sparse(w)

运行结果：

 或者这样创建稀疏矩阵：

clear all
clc
%sparse([起点集合],[对应终点集合],[对应权重集合])
G = sparse([1 1 1 2 2],[2 3 4 3 4],[2 3 8 6 6]);
s=sparse(G)

运行结果：  可以看出与上面一样

2.1.2 有向图最短路径（1）

使用函数：graphallshortestpaths，其语法如下：

参数含义：
G:稀疏矩阵
0/false代表无向图 1/true代表有向图。默认为true。

我们要解决如下问题：
首先创建一个有向图：

代码：

clear all
clc
G = sparse([6 1 2 2 3 4 4 5 5 6 1],[2 6 3 5 4 1 6 3 4 3 5],[41 99 51 32 15 45 38 32 36 2