三角函数对应在平面坐标上画圆

目录

1、圆半径(r)为 : 1

2、圆半径(r)为 : r

3、例程

---

        三角函数（Trigonometric Functions）是基本初等函数之一，是以角度（数学上最常用弧度制，下同）为自变量，角度对应任意角终边与单位圆交点坐标或其比值为因变量的函数。

        三角函数将直角三角形的内角和它的两个边的比值相关联，也可以等价地用与单位圆有关的各种线段的长度来定义。三角函数在研究三角形和圆等几何形状的性质时有重要作用，也是研究周期性现象的基础数学工具。

1、圆半径(r)为 : 1

        在屏幕上绘制圆时，一般情况是在对应的 X 与 Y 点进行点的绘制，在 “ 图1 ” 中我们可以看出在平面坐标系中的 x 与 y 坐标的关系式为：（ y = sinθ ） 与 （ x = cosθ ），通过该关系式我们可以改变  角度值 (θ) 来确定对应的 x 与 y 坐标，然后通过对应的关系把平面坐标上的 x 与 y 转化成屏幕上的 X 与 Y 点即可完成圆的绘制。

        注意：角度值需要换成正弦、余弦值，所以最后的关系式变为：“ y = sin(θ*3.14/180) ” 与 “ x = cos(θ*3.14/180) ” 

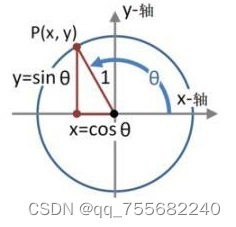
 图1

        对应的三角函数表格：

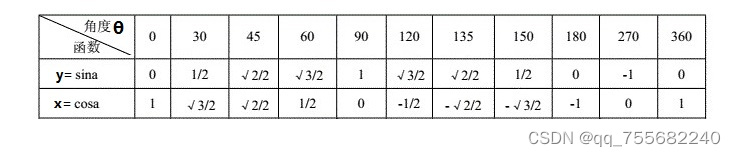
2、圆半径(r)为 : r

        上面的平面坐标关系式是基于 半径(r) 为 1 时的关系式，正常情况下我们的半径是变化的由此上面的关系式则需要乘以 半径(r) ，如 “ 图2 ” 所示。我们可以看出在平面坐标系中的 x 与 y 坐标的关系式为：（ y = sinθ * r ） 与 （ x = cosθ * r ）。通过该关系式我们可以改变  角度值 (θ) 来确定对应的 x 与 y 坐标，然后通过对应的关系把平面坐标上的 x 与 y 转化成屏幕上的 X 与 Y 点即可完成圆的绘制。

        注意：角度值需要换成正弦、余弦值，所以最后的关系式变为：“ y = sin(θ*3.14/180)*r ” 与 “ x = cos(θ*3.14/180)*r ” 

 图2

3、例程

        Bresenham画圆算法也称为中点画圆算法，与Bresenham 直线算法一样，其基本的方法是利用判别变量来判断选择最近的像素点，判别变量的数值仅仅用一些加、减和移位运算就可以计算出来。该算法巧妙的利用了圆的八对称性，只计算出一个八分周上的点，其余的七个点利用对称性即可得出。

#define     LCD_Width     128
#define     LCD_Height    64

/**
 * @breif	画圆函数
 * @param   x1,x2 —— 圆心坐标
 * @param	r     —— 半径
 * @retval	none
 */
void LCD_Draw_ColorCircle(uint16_t x, uint16_t y, uint16_t r)
{
	/* Bresenham画圆算法 */
	int16_t a = 0, b = r;
    int16_t d = 3 - (r << 1);		//算法决策参数
		
	/* 如果圆在屏幕可见区域外，直接退出 */
    if (x - r < 0 || x + r > LCD_Width || y - r < 0 || y + r > LCD_Height) 
				return;
		
	/* 开始画圆 */
    while(a <= b)
    {
        LCD_Draw_ColorPoint(x - b, y - a);//调用画点函数
        LCD_Draw_ColorPoint(x + b, y - a);//调用画点函数
        LCD_Draw_ColorPoint(x - a, y + b);//调用画点函数
        LCD_Draw_ColorPoint(x - b, y - a);//调用画点函数
        LCD_Draw_ColorPoint(x - a, y - b);//调用画点函数
        LCD_Draw_ColorPoint(x + b, y + a);//调用画点函数
        LCD_Draw_ColorPoint(x + a, y - b);//调用画点函数
        LCD_Draw_ColorPoint(x + a, y + b);//调用画点函数
        LCD_Draw_ColorPoint(x - b, y + a);//调用画点函数
        a++;

        if(d < 0)
			d += 4 * a + 6;
        else
        {
            d += 10 + 4 * (a - b);
            b--;
        }

        LCD_Draw_ColorPoint(x + a, y + b);//调用画点函数
    }
}