素性测试
素性测试就是给定一个正整数,然后判断其是否有真因数(除了1和它本身之外的其他正整数)
确定性测试
确定性测试是能够肯定该数的素性,
从2开始到 N \sqrt{N} N用每个数遍历去和N比划比划,要是能被N整除开则表明N不是素数
优点是确定性
缺点是当N很大的时候时间复杂度大
概率性测试
挑选任意几个数去和N比划比划,如果N能够整除则N一定不是素数.否则N可能是素数
缺点:只能够从概率上保证整数的素性,一个整数通过几次素性测试,只能表明其是一个素数的概率比较大,但是不能断定其就是一个素数
优点:但是如果试验次数够多的话可以极大似然地认为该数就是一个素数.并且时间复杂度要比遍历低得多
比如Fermat素性测试和Miller-Rabin素性测试
文章目录
Fermat素性测试
费马小定理:
p p p是一个素数,对于任意整数a,都有 a p − 1 ≡ 1 ( m o d p ) a^{p-1}\equiv 1\ (\mod p) ap−1≡1 (modp)
用快速幂计算 a p − 1 m o d p a^{p-1}\mod p ap−1modp
#include <iostream>
#include <algorithm>
using namespace std;
int quick_pow(const int &base, const int &index, const int &p) {
if (index == 0)
return 1;
else if (index == 1)
return base % p;
else if (index % 2) {
int temp = base * base % p;
return quick_pow(temp, index >> 1, p) * base % p;
} else {
int temp = base * base % p;
return quick_pow(temp, index >> 1, p);
}
}
const int p = 31;
int main() {
for (int i = 2; i < p; ++i) {
cout << quick_pow(i, p - 1, p) << " ";
}
return 0;
}
选定 p = 31 p=31 p=31做实验
运行结果
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
均满足费马小定理
选定 N = 30 N=30 N=30做实验
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
费马小定理逆定理不成立
即如果对于任选的 a a a,都有 a p − 1 ≡ 1 ( m o d N ) a^{p-1}\equiv 1(\mod N) ap−1≡1(modN),不能说明N是一个素数
伪素数
比如
N
=
341
,
a
=
2
N=341,a=2
N=341,a=2
2
340
≡
1
(
m
o
d
341
)
2^{340}\equiv 1(\mod 341)
2340≡1(mod341)
但是
N
=
341
=
11
×
31
N=341=11\times 31
N=341=11×31不是素数,因此N被称为"伪素数"
这里只是取了一个 a = 2 a=2 a=2,如果取一个 a = 3 a=3 a=3则有 3 340 ≡ 5 ( m o d 341 ) 3^{340} \equiv 5(\mod 341) 3340≡5(mod341),立刻判定341不是素数
于是对于这种情况我们只需要多取几次a去试就可以判定 N N N是不是素数
还是 N = 341 N=341 N=341用刚才的程序计算
卡迈尔克数
但是,就是有这么一类数,你使劲取 a a a,只要是 a a a和 N N N互素,它都装的跟个孙子一样,都满足 a N − 1 ≡ 1 ( m o d N ) a^{N-1}\equiv 1(\mod N) aN−1≡1(modN),但是N就不是素数
他们叫"卡迈克尔数", 561 = 3 ∗ 11 ∗ 17 561=3*11*17 561=3∗11∗17就是一个
用下列这些数字去测试561都会得到 a 560 ≡ 1 ( m o d 561 ) a^{560}\equiv 1(\mod 561) a560≡1(mod561),这些数字都满足 g c d ( a , 561 ) = 1 gcd(a,561)=1 gcd(a,561)=1
2 4 5 7 8 10 13 14 16 19 20 23 25 26 28 29 31 32 35 37 38 40 41 43 46 47 49 50 52 53 56 58 59 61 62 64 65 67 70 71 73 74 76 79 80 82 83 86 89 91 92 94 95 97 98 100 101 103 104 106 107 109 112 113 115 116 118 122 124 125 127 128 130 131 133 134 137 139 140 142 145 146 148 149 151 152 155 157 158 160 161 163 164 166 167 169 172 173 175 178 179 181 182 184 185 188 190 191 193 194 196 197 199 200 202 203 205 206 208 211 212 214 215 217 218 223 224 226 227 229 230 232 233 235 236 239 241 244 245 247 248 250 251 254 256 257 259 260 262 263 265 266 268 269 271 274 277 278 280 281 283 284 287 290 292 293 295 296 298 299 301 302 304 305 307 310 311 313 314 316 317 320 322 325 326 328 329 331 332 334 335 337 338 343 344 346 347 349 350 353 355 356 358 359 361 362 364 365 367 368 370 371 373 376 377 379 380 382 383 386 388 389 392 394 395 397 398 400 401 403 404 406 409 410 412 413 415 416 419 421 422 424 427 428 430 431 433 434 436 437 439 443 445 446 448 449 452 454 455 457 458 460 461 463 464 466 467 469 470 472 475 478 479 481 482 485 487 488 490 491 494 496 497 499 500 502 503 505 508 509 511 512 514 515 518 520 521 523 524 526 529 530 532 533 535 536 538 541 542 545 547 548 551 553 554 556 557 559 560
共319个
也就是说每次任选一个 a ∈ [ 2 , 560 ] a\in[2,560] a∈[2,560],去测试561的素性,失误概率为 319 559 = 0.570661896243292 \frac{319}{559}=0.570661896243292 559319=0.570661896243292
假设试验k次,那么全都失败的概率是 0.5 7 k 0.57^k 0.57k,成功概率为 1 − 0.5 7 k 1-0.57^k 1−0.57k
如果使成功概率在 90 90% 90以上,即令 1 − 0.5 7 k ≥ 0.9 1-0.57^k\ge 0.9 1−0.57k≥0.9解得到 4.09 4.09 4.09
即尝试4次之后就可以有比较高的把握,决定这个数是素数还是合数了
Miller-Rabin素性测试
费马小定理"逆定理"起死回生
虽然费马小定理的逆定理不成立,但是,如果素性测试次数多了,也能够以很高的概率认为一个数是否是素数
即虽然逆定理不成立但是仍然有一定的利用价值
感觉类似于SSA无法判定全等,但是能够在一定程度上确定三角形的形状
我们现在认为,如果任取 a a a,在我们选取的这几次a中,都满足 a N − 1 ≡ 1 ( m o d N ) a^{N-1}\equiv 1(\mod N) aN−1≡1(modN),则概率认为N是素数
而这样做也是有道理的,刚才卡迈尔克数561在进行4次素性测试之后被测试出是合数的概率已经达到了 90 90% 90
现在问题是,如何科学的选取 a a a
需要用到二次探测定理
二次探测定理
如果 p p p是一个奇素数,则 x 2 ≡ 1 ( m o d p ) x^2\equiv 1(\mod p) x2≡1(modp)的解为 x ≡ 1 ( m o d p ) x\equiv 1(\mod p) x≡1(modp)或者 x ≡ p − 1 ( m o d p ) x\equiv p-1(\mod p) x≡p−1(modp)
证明:
由 x 2 ≡ 1 ( m o d p ) x^2\equiv 1(\mod p) x2≡1(modp)得到 x 2 − 1 ≡ 0 ( m o d p ) x^2-1\equiv 0(\mod p) x2−1≡0(modp),即 ( x + 1 ) ( x − 1 ) ≡ 0 ( m o d p ) (x+1)(x-1)\equiv 0(\mod p) (x+1)(x−1)≡0(modp)
即 p ∣ ( x + 1 ) ( x − 1 ) p|(x+1)(x-1) p∣(x+1)(x−1),即 ( x + 1 ) ( x − 1 ) = k p , k ∈ Z , k ≠ 0 (x+1)(x-1)=kp,k\in Z,k≠0 (x+1)(x−1)=kp,k∈Z,k=0
又 p p p是一个素数因此两个乘数之一必然包含 p p p这个因子,
当 x + 1 x+1 x+1包含p因子时得到 p ∣ ( x + 1 ) p|(x+1) p∣(x+1),即 x + 1 ≡ 0 ( m o d p ) x+1\equiv 0(\mod p) x+1≡0(modp),即 x ≡ − 1 ( m o d p ) x\equiv -1(\mod p) x≡−1(modp),即 x ≡ p − 1 ( m o d p ) x\equiv p-1(\mod p) x≡p−1(modp)
当 x − 1 x-1 x−1包含p因子时得到 p ∣ ( x − 1 ) p|(x-1) p∣(x−1),即 x − 1 ≡ 0 ( m o d p ) x-1\equiv 0(\mod p) x−1≡0(modp),即 x ≡ 1 ( m o d p ) x\equiv 1(\mod p) x≡1(modp)
考虑什么是"奇素数",很庆幸的是除了2之外其他的偶数都是合数,那么奇素数就是除了2之外的任何素数
那么这个定理的适用范围就很广了
二次探测定理+费马小定理"逆定理"
1.假设 N N N是一个待测试的整数(N>2),我们期望他是一个素数,
基于上述期望,素数N一定是奇数,那么 N − 1 N-1 N−1是一个偶数
2.考虑一个偶数可以分解成一伙子2和一个奇数的乘积
比如 48 = 16 ∗ 3 = 2 4 ∗ 3 48=16*3=2^4*3 48=16∗3=24∗3,比如 30 = 2 ∗ 15 30=2*15 30=2∗15
则一个偶数可以写为 e v e n = a × 2 b even=a\times 2^b even=a×2b,其中a是一个奇数
而 N − 1 N-1 N−1也是偶数,当然也可以写成 N − 1 = a × 2 b N-1=a\times 2^b N−1=a×2b
3.任取一个 x x x,去和N比划比划即通过 x N − 1 ≡ 1 ( m o d N ) x^{N-1}\equiv 1(\mod N) xN−1≡1(modN)去验证N是否是一个素数
即 x N − 1 − 1 m o d N x^{N-1} -1\mod{N} xN−1−1modN通过快速幂计算判断结果是否为0
而
N
−
1
=
a
×
2
b
N-1=a\times 2^b
N−1=a×2b带入上式
x
a
×
2
b
−
1
m
o
d
N
=
(
(
x
a
)
2
b
−
1
)
2
−
1
m
o
d
N
=
(
(
x
a
)
2
b
−
1
+
1
)
(
(
x
a
)
2
b
−
1
−
1
)
m
o
d
N
=
(
(
x
a
)
2
b
−
1
+
1
)
(
(
x
a
)
2
b
−
2
+
1
)
(
(
x
a
)
2
b
−
2
−
1
)
m
o
d
N
=
.
.
.
=
(
(
x
a
)
2
b
−
1
+
1
)
(
(
x
a
)
2
b
−
2
+
1
)
.
.
.
(
x
a
+
1
)
(
x
a
−
1
)
m
o
d
N
\begin{aligned} &x^{a\times 2^b}-1\mod N\\ &=((x^a)^{2^{b-1}})^2-1\mod N\\ &=((x^a)^{2^{b-1}}+1)((x^a)^{2^{b-1}}-1)\mod N\\ &=((x^a)^{2^{b-1}}+1)((x^a)^{2^{b-2}}+1)((x^a)^{2^{b-2}}-1)\mod N\\ &=...\\ &=((x^a)^{2^{b-1}}+1)((x^a)^{2^{b-2}}+1)...(x^a+1)(x^a-1)\mod N \end{aligned}
xa×2b−1modN=((xa)2b−1)2−1modN=((xa)2b−1+1)((xa)2b−1−1)modN=((xa)2b−1+1)((xa)2b−2+1)((xa)2b−2−1)modN=...=((xa)2b−1+1)((xa)2b−2+1)...(xa+1)(xa−1)modN
如果最后的因数分解式中有一项为0则认为通过了该次素性测试
4.由二次探测定理有
x
a
m
o
d
N
=
1
x
a
m
o
d
N
=
N
−
1
(
x
a
)
2
m
o
d
N
=
N
−
1
.
.
.
(
x
a
)
2
b
−
1
m
o
d
N
=
N
−
1
\begin{aligned} x^a \mod N&=1\\ x^a\mod N&=N-1\\ (x^a)^2\mod N&=N-1\\ ...\\ (x^a)^{2^{b-1}}\mod N&=N-1 \end{aligned}
xamodNxamodN(xa)2modN...(xa)2b−1modN=1=N−1=N−1=N−1
这其中有一个式子成立即可
如果这些式子都没有成立则可以啃腚N不是素数
即满足费马小定理"逆定理"的不一定是素数,但是不满足费马小定理"逆定理"的一定不是素数
算法实现
int gcd(const int &a, const int &b) {
if (b == 0)
return a;
return gcd(b, a % b);
}
int quick_pow(const int &base, const int &index, const int &p) {
if (index == 0)
return 1;
else if (index == 1)
return base % p;
else if (index % 2) {
int temp = base * base % p;
return quick_pow(temp, index >> 1, p) * base % p;
} else {
int temp = base * base % p;
return quick_pow(temp, index >> 1, p);
}
}
int miller_rabin(const int &n) {
if (n < 3 || n % 2 == 0)
return 2;
int a = n - 1;
int b = 0;
while (a % 2 == 0) {
++b;
a /= 2;
}
//到此n-1=a*2^b
const int trial_times = 10;
int x;
int base;
for (int i = 0; i < trial_times; ++i) {
x = rand() % (n - 2) + 2; //限制x∈[2,n-1]
int base = quick_pow(x, a, n); //base=x^a
if (base == 1)
continue;//如果x=1(mod n)则直接通过本次素性测试
int j;
for (int j = 0; j < b; ++j) {
if (base == n - 1)
break;//base=n-1(mod n)通过本次素性测试
base = (long long)base * base % n;
}
if (j >= b)
return 0;//本次所有所有机会都没有把握住,未通过素性测试
}
return 1;//通过所有trial_times次素性测试,概率认为n是素数
}
BUUCTF-Alice和Bob
分解质因数98554799767
得到因子101999去做试验
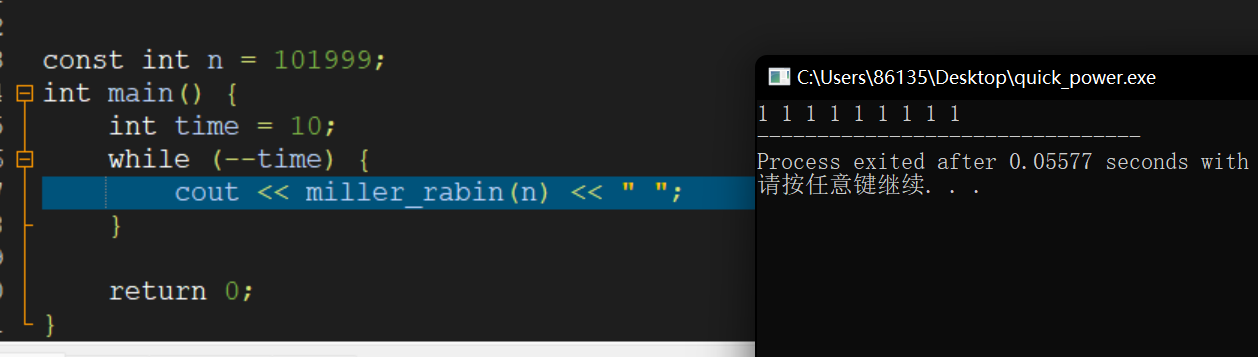



























 7729
7729

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










