三相H桥SVPWM算法介绍

我见过有SVPWM有用于单相H桥逆变的、三电平逆变器、多电平逆变器的。这里着重点用于三相H桥逆变器。他们不同之处在于，开关状态越多，空间矢量图越大。

1 算法介绍

下图是三相H逆变器拓扑结构

以下是直流无刷电机的简化逻辑结构。图中，由于控制电机的电路是三相H桥逆变电路，故用三位数字表达H桥的导通状态，分别表示a相、b相、c相。

总的来说，就是旋转的磁场可以引导转子旋转。要理解上图，推荐下载硬石STM32的开源资料。理解直流无刷电机之前，我觉得需要学习两相步进电机。

上面的三项H桥拓扑结构，调制方式主要分为SPWM和SVPWM。SVPWM英文名是space-vector pulse width modulation。空间矢量的概念，需要结合电机磁场的旋转来理解。我们需要合成一个稳定旋转的磁场，牵引转子的旋转。合成磁场的方向，和abc三相的电流导通模式有关，影响着电机转动的方向；而合成磁场的大小，和绕组中导通电流有关，会影响转动力矩。

2 算法的实现过程

2.1 坐标变换

2.1.1 alpha-beta坐标轴转换为abc

2.1.2 Abc坐标轴转换为alpha-beta

2.2 矢量合成

本逆变器的开关管只有6个，可以用8个空间矢量描述逆变器的开关状态。Vref为参考矢量，代表着定子绕组通电形成的合成磁场的大小和方向。Ts是采样周期。把8个空间矢量分别标号，V1为100，V2：110，V3：010，V4：011，V5：001，V6：101，V7:111，V0：000。

上图，可以进一步转化为下图的形式。参考矢量Vref可以当作是转子的旋转磁场。

上图称为逆变器的空间矢量图。

空间矢量图被空间矢量划分为6个扇区，分别命名为第I扇区、第II扇区、第III扇区、第IV扇区、第V扇区、第VI扇区。

顺时针旋转，参考矢量会分别经过第I扇区、第VI扇区、第V扇区、第IV扇区、第III扇区、第II扇区。

逆时针旋转，参考矢量会分别经过第I扇区、第II扇区、第III扇区、第IV扇区、第V扇区、第VI扇区。

当参考矢量旋转到第I扇区，可以用V1、V2、V7、V0四个空间矢量合成参考矢量，但是要先通过调整占空比，把矢量幅值缩小。

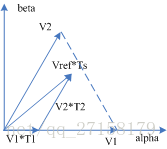
根据伏秒平衡，可得以下公式。

公式中，V1、V2、V0是用于合成参考矢量的作用矢量。T1、T2、T0分别是V1、V2、V0的作用时间。Ts是采样周期。

因为逆变器的状态只有8种，假如需要无限逼近参考矢量，则要用很高频率的PWM波。

 

2.2.1 时间计算-第I扇区

 

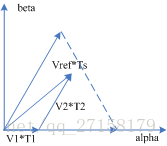
代入

可得

2.2.2 时间计算-第II扇区

 

2.2.3 时间计算-第III扇区

2.2.4 时间计算-第IV扇区

2.2.5 时间计算-第V扇区

2.2.6 时间计算-第VI扇区

 

 

2.3 发出PWM

上面介绍默认SVPWM使用三段式模式，在Ts采样周期内，首先V0作用T0时间，然后V1作用T1时间，最后V2作用T2时间。接下来是下一个Ts时间段。

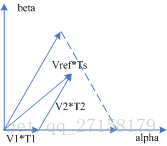
V0->V1->V2

以下是五段式：

V0->V1->V2->V1->V0

以下是七段式：

V0->V1->V2->V7->V2->V1->V0

这种过渡，一方面可以减少低频谐波、降低滤波器的设计难度；另一方面，可以降低开关在切换过程中的电压变化。

 

下一步是在STM32中实现本算法……

 

开源了SVPWM算法，但是未测试验证过，硬件上手头只有STM32的最小系统板，就暂时没做实验了。

https://github.com/xxJian/STM32_Based_SVPWM