判断一个点是否在多边形内部 - 射线法思路

原文链接

判断一个点是否在多边形内部 [1] 射线法思路、
判断一个点是否在多边形内部 [2] 射线法实现

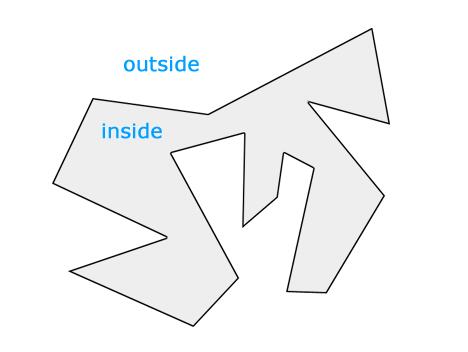
比如说，我就随便涂了一个多边形和一个点，现在我要给出一种通用的方法来判断这个点是不是在多边形内部（别告诉我用肉眼观察……）。

首先想到的一个解法是从这个点做一条射线，计算它跟多边形边界的交点个数，如果交点个数为奇数，那么点在多边形内部，否则点在多边形外。

这个结论很简单，那它是怎么来的？下面就简单讲解一下。

首先，对于平面内任意闭合曲线，我们都可以直观地认为，曲线把平面分割成了内、外两部分，其中“内”就是我们所谓的多边形区域。

基于这一认识，对于平面内任意一条直线，我们可以得出下面这些结论：

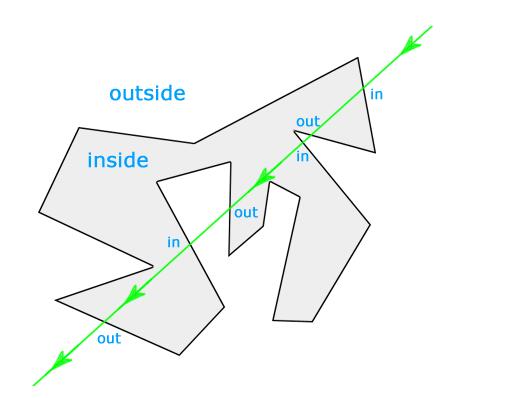
直线穿越多边形边界时，有且只有两种情况：进入多边形或穿出多边形。
在不考虑非欧空间的情况下，直线不可能从内部再次进入多边形，或从外部再次穿出多边形，即连续两次穿越边界的情况必然成对。
直线可以无限延伸，而闭合曲线包围的区域是有限的，因此最后一次穿越多边形边界，一定是穿出多边形，到达外部。

现在回到我们最初的题目。假如我们从一个给定的点做射线，还可以得出下面两条结论：

如果点在多边形内部，射线第一次穿越边界一定是穿出多边形。
如果点在多边形外部，射线第一次穿越边界一定是进入多边形。

把上面这些结论综合起来，我们可以归纳出：

当射线穿越多边形边界的次数为偶数时，所有第偶数次（包括最后一次）穿越都是穿出，因此所有第奇数次（包括第一次）穿越为穿入，由此可推断点在多边形外部。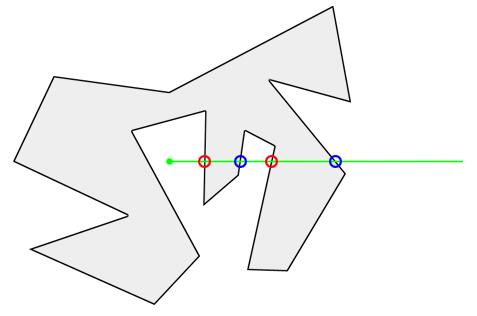
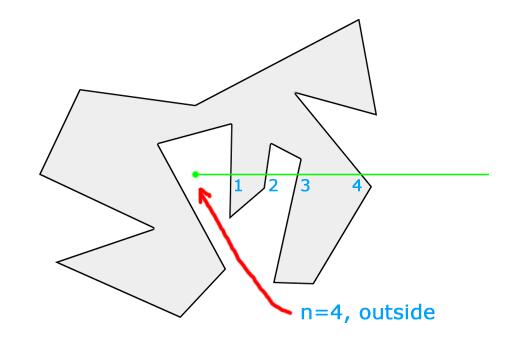
当射线穿越多边形边界的次数为奇数时，所有第奇数次（包括第一次和最后一次）穿越都是穿出，由此可推断点在多边形内部。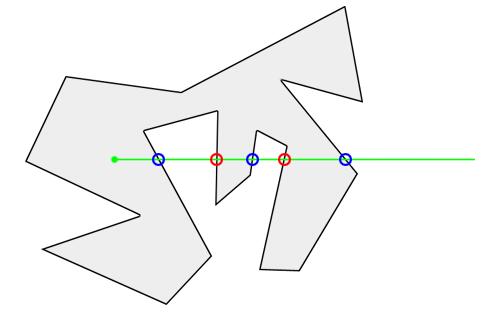
到这里，我们已经了解了这个解法的思路，大家可以试着自己写一个实现出来。

---

不知道大家思考得怎么样，有没有遇到一些不好处理的特殊情况。今天就来讲讲射线法在实际应用中的一些问题和解决方案。

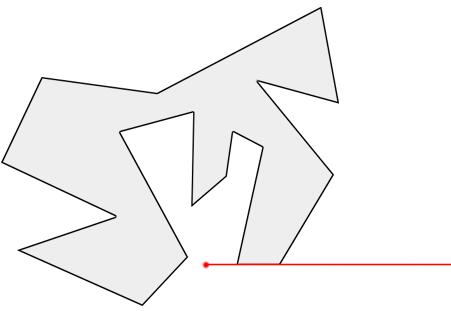
1点在多边形的边上

前面我们讲到，射线法的主要思路就是计算射线穿越多边形边界的次数。那么对于点在多边形的边上这种特殊情况，射线出发的这一次，是否应该算作穿越呢？

看了上面的图就会发现，不管算不算穿越，都会陷入两难的境地——同样落在多边形边上的点，可能会得到相反的结果。这显然是不正确的，因此对这种特殊情况需要特殊处理。

2点和多边形的顶点重合

这其实是第一种情况的一个特例。

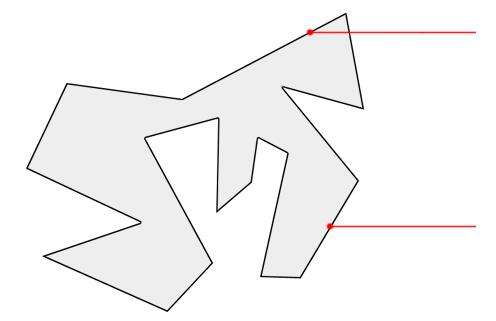
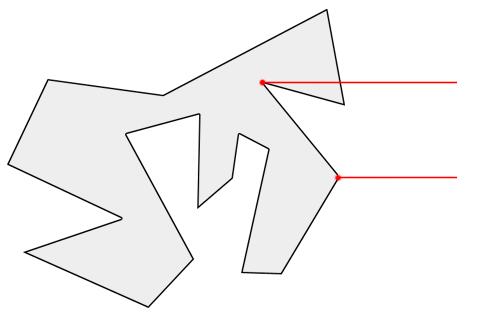
3射线经过多边形顶点

射线刚好经过多边形顶点的时候，应该算一次还是两次穿越？这种情况比前两种复杂，也是实现中的难点，后面会讲解它的解决方案。

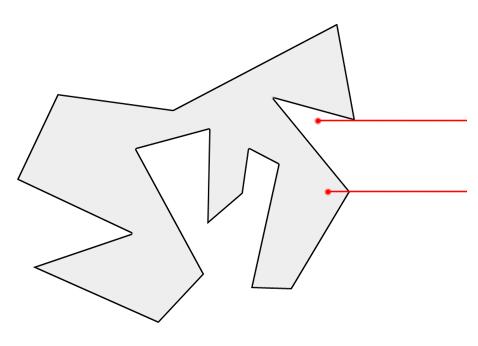
4射线刚好经过多边形的一条边

这是上一种情况的特例，也就是说，射线连续经过了多边形的两个相邻顶点。

解决方案：

1判断点是否在线上的方法有很多，比较简单直接的就是计算点与两个多边形顶点的连线斜率是否相等，中学数学都学过。

2点和多边形顶点重合的情况更简单，直接比较点的坐标就行了。

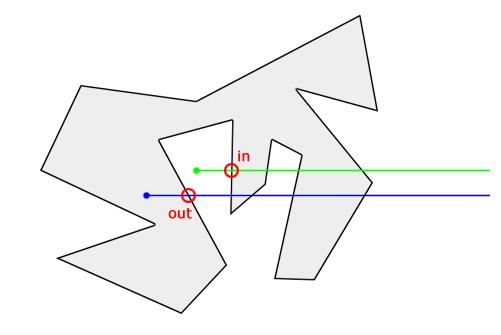
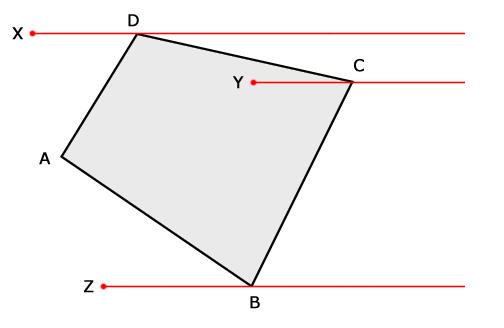
3顶点穿越看似棘手，其实我们换一个角度，思路会大不相同。先来回答一个问题，射线穿越一条线段需要什么前提条件？没错，就是线段两个端点分别在射线两侧。只要想通这一点，顶点穿越就迎刃而解了。这样一来，我们只需要规定被射线穿越的点都算作其中一侧。

如上图，假如我们规定射线经过的点都属于射线以上的一侧，显然点D和发生顶点穿越的点C都位于射线Y的同一侧，所以射线Y其实并没有穿越CD这条边。而点C和点B则分别位于射线Y的两侧，所以射线Y和BC发生了穿越，由此我们可以断定点Y在多边形内。同理，射线X分别与AD和CD都发生了穿越，因此点X在多边形外，而射线Z没有和多边形发生穿越，点Z位于多边形外。

解决了第三点，这一点就毫无难度了。根据上面的假设，射线连续经过的两个顶点显然都位于射线以上的一侧，因此这种情况看作没有发生穿越就可以了。由于第三点的解决方案实际上已经覆盖到这种特例，因此不需要再做特别的处理。