异常值是指距离其他观测值非常遥远的点,但是我们应该如何度量这个距离的长度呢?同时异常值也可以被视为出现概率非常小的观测值,但是这也面临同样的问题——我们要如何度量这个概率的大小呢?
有许多用来识别异常值的参数和非参数方法,参数方法需要一些关于变量分布情况的假设条件,而非参数方法并不需要这些假设条件。此外,你还可以利用单变量分析和多变量分析的方法来识别异常值。
那么问题来了,哪个方法得到的结果才是正确的呢?不幸的是,实际上并不存在唯一的标准答案,结果的正确与否取决于你识别这些异常值的目的。你可能想要单独分析某个变量的情况,或者想利用这些变量构建预测模型。
让我们采用更直观的方法来识别异常值吧。
假设存在一个关于移动应用程序的数据集,其中包括操作系统、用户收入和设备情况三个变量,如下图所示:

我们应该如何识别出收入变量的异常值呢?
接下来我将尝试利用参数和非参数方法来检测异常值。
参数方法

如上图所示,x轴中的变量是收入,y轴代表收入值对应的概率密度值。图中粉色部分代表真实的样本数据,绿色部分表示正态分布数据,蓝色部分代表对数正态分布数据。其中正态分布和对数正态分布数据与实际样本数据具有相同的均值和方差。
我们可以通过计算观测值出现的概率或者计算观测值与均值之间的距离来判断异常值的情况。比如,正态分布情况下位于距均值三倍标准差范围外的观测值被视为异常值。
上述的例子中,如果我们假设原始数据服从正态分布,那么收入大于60,000元的数据都被视为异常值。从右图中可以看出,对数正态分布能更好地识别出真实的异常值,这是因为原始数据的分布近似于服从对数正态分布。但这并不是一个通用的方法,因为我们很难事先判断出数据潜在的分布情况。我们可以通过数据的拟合曲线来判断参数情况,但是如果原始的数据发生了变化,那么分布的参数也会随之发生改变。

上图展示了概率密度函数如何随参数的变化而发生改变,我们可以很明显地看出参数的变化会影响异常值的识别过程。
非参数方法
首先让我们来看一个识别异常值的简单的非参数方法——箱线图:

如上图所示,我们可以看出数据中存在 7 个显著的异常值(绿色标记的数据)。更多关于箱线图的内容请参考这篇文章。
上文提到的数据集中还存在一个分类变量——操作系统。如果我们根据操作系统将数据分组并绘制箱线图,那么我们是否能够识别出相同的异常值呢?

上图中,我们采用了多变量分析的方法。从图中我们可以看出,IOS 组中存在 3 个异常值,而安卓组则没有检测出异常值。这是因为安卓用户和 IOS 用户的收入分布情况不一致,所以如果只利用单变量分析方法的话,我们将会错误地识别出异常值。
结论
我们可以利用基于数据潜在分布情况的参数和非参数方法来检测异常值。在样本数据的均值十分贴近于分布函数的中心且数据集足够大的情况下,我们可以利用参数方法来识别异常值。如果中位数比均值更贴近于数据的分布中心,那么我们应该利用非参数的方法来识别异常值。
接下来我们将介绍如何利用聚类方法识别多变量情形中的异常值。
顾名思义,聚类方法就是将特征相似的样本聚集在同一个类别中,因此样本间的相似性是一个非常重要的概念,我们需要考虑如何量化样本间的相似情况。通常情况下,我们用样本之间的距离远近来衡量其相似度,不同的聚类方法采用不同的距离测度方式来实现聚类的目标。我们应该着重关注一个被广泛使用的聚类方法——K均值聚类算法。
K均值聚类算法主要是基于两两样本之间的欧式距离,欧式距离是两点之间的直线距离。我们还可以采用其他方法——比如马氏距离,闵式距离和切比雪夫距离——来度量样板间的相似性,但是这些方法的缺点是计算量大、收敛速度较慢。
给定一组样本x1,x2,…,xn,其中每个观测值都是一个d维的向量,K均值算法的目标是在最小化类内离差的前提下将这n个观测值分成 k(<=n) 组(S={S1,S2,…,Sk})。换句话说,该算法的目标函数如下所示:

其中μi表示第 i 组样本的均值。
借助上面这个目标函数,我们可以更加直观地介绍K均值算法的计算过程。
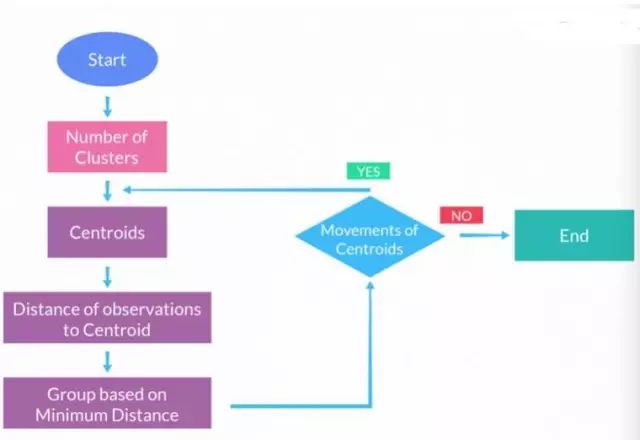
K均值算法的基本步骤
步骤一:聚类数目
选择类别数目k。这是一个循环迭代的过程,我们无法提前知道应该选择聚成几个类别。我们将用一个例子来说明如何选择类别数目。
步骤二:聚类中心
从样本中随机抽取出k个点,并将其定义为k个组的中心。
步骤三:计算距离
分别计算所有观测值到聚类中心的欧式距离,并将其归到距离最近的中心类别中。假设我们有一个包含100个观测值的数据集,我们的目标是将其聚成5类。首先我们需要计算每个观测值到5个中心点的距离,然后从5个距离中筛选出距离最小值,并将该样本归到对应的类别中。
步骤四:重新计算类中心
接下来我们需要重新计算各个类别的中心值。某个类的中心值等于该类别中所有样本点的均值。因此,如果某个类别中的样本点由于步骤三的计算导致了重分配,那么相应的类中心也会随之改变。
步骤五:迭代过程
重复步骤三和步骤四直到类别中心不再改变为止。
拟合K均值算法前需要记住一个要点——对变量进行标准化处理。比如,你的数据集中包含年龄、身高、体重、收入等无法直接比拟的变量,我们需要将其标准化到同一量纲中。如果数据集中的变量单位一致但方差不同,我们也需要事先将其标准化。数据集中的变量方差不相等,这相当于对方差小的变量赋予了一个更大的权重,因此该算法倾向于对方差大的变量进行划分。标准化处理可以保证K均值算法同等对待所有的变量。一个常用的标准化方法是——所有的观测值减去均值然后除以标准差。
接下来,让我们利用K均值聚类算法来识别数据集中的异常值。假设数据集中某一个类别的特征完全不同于其他类别,如下表所示:
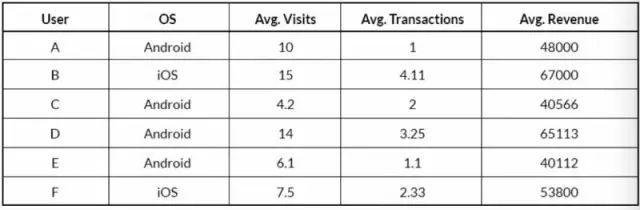
上表是某个 app 的部分用户数据。表中有 5 个变量,其中 3 个数值变量,2 个分类变量。分析过程中,我们将忽略第一列变量。通常情况下,我们将 OS 变量中的 Android 赋值为 0,iOS 赋值为1。但是从理论上来说,我们并不建议这样做,因为拟合K均值模型需要计算样本之间的欧式距离,我们无法很好地量化 Android 用户和 iOS 用户之间的距离。
举个例子,如果点 A 和点 B 之间的欧式距离等于 30,点 A 和点 C 之间的欧式距离等于 8,那么我们可以推出点 A 和点 C 更相似。但分类变量不是由数值构成的,而是由枚举的方式展现出来,比如“香蕉”、“苹果”和“橙子”,我们无法计算这些水果之间的欧式距离,所以我们无法判断橙子和香蕉哪个与苹果更相近。基于这个原因,我们应该采用K众数算法来处理分类变量问题,而不是K均值算法。
获取聚类数目是一个反复迭代的过程。为了获取最佳类别数目,我们可以尝试对所有的样本分别拟合 2-20 个类别的模型,然后通过评估统计量的表现情况来选取最佳类别数目。作为一名分析师,拟合多少个类别的模型都是由你决定的。但需要注意的是,你必须在建模前标准化处理数据。
我们可以利用一些统计量来评估最佳类别数目,比如类内平方和,类间平方和,方差贡献比和统计差异值。本文中主要采用类内平方和来选择最佳类别数目。
类内平方和(wss)
类内平方和主要反映同一类别中样本的同质性,该统计量通过计算类中所有点与类中心之间的距离平方和来刻画聚类效果。加总所有类的类内平方和得到所有样本的总离差平方和(Total wss)。
上述指标是个相对指标而不是绝对指标,也就是说我们需要结合类别数目来进一步判断最佳类别数目。如果我们的最佳类别数目在 2 和 20 之间,那么我们倾向于选择具有最小 twss 的类别数目。
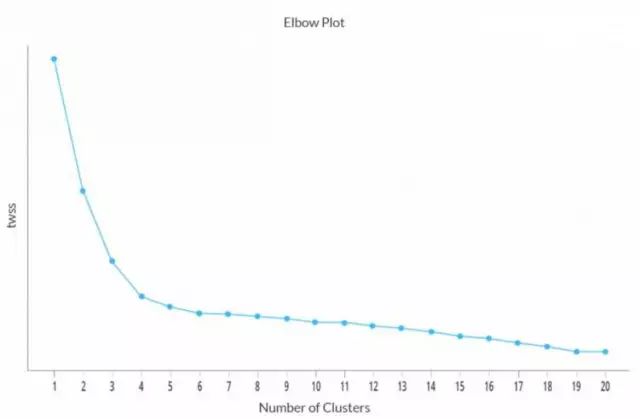
上图展现了 twss 随类别数目变化的趋势图,从图中可以看出:当类别数目大于4时,twss的下降率大大降低。理论上来说,你会倾向于选择最小twss所对应的类别数目,但在实际应用中这并不是一个好的方案;虽然将样本聚成 19 类时具有最小的 twss,但是分析这么多类的数据非常麻烦,我们无法达到聚类的基本要求——类内差异小,类间差异大。综合多方面信息,本例中我们应该选择的最佳类别数目为 4。你甚至可以比较不同类别数目模型之间的差异,然后再选取出最佳类别数目。
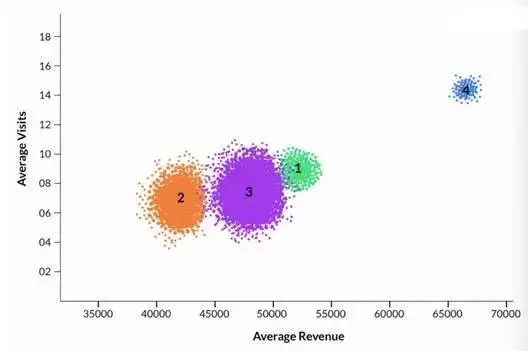
上图中不同颜色的点代表不同类别中的样本。其中第 4 类不同于其他三个类,它的标记颜色为蓝色。
聚类特征

上表给出了每个类别中观测值的数量,其中类别 4 占比最小,仅为 3.7%。
接下来让我们看看每个类别各自的一些特征:

上表不仅给出了每个类别中各个变量的均值以及样本的总体均值和标准差,同时还提供了一个用于衡量类均值与总体均值之间差异的统计量 Z-score:
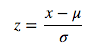
其中μ代表总体均值,σ代表总体标准差。
对每个数值型变量来说,标准差越小,对应的 Z-score 越大。Z-score 的符号代表类均值高于或低于总体均值。
第 4 类的变量值与其他三个类别相差甚远,比如较低的样本个数,较高的访问量、交易值和 Z-score。
让我们也来看看不同类别中分类变量 OS 的差异情况:

从上表中可以看出,第 4 类中 iOS用户的比例远高于其他三组,因此我们可以认为第 4 类为异常值。作为一名分析师,我们需要进一步探索第 4 类的详细情况,以便于更好地了解异常值的情况。
总之,我们可以利用聚类方法来识别多变量情形中的异常值。除了K均值算法外还有许多聚类算法可以用于检测异常值,但这些已经超出了本文的讨论范围。
























 973
973

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








