线性代数复习一——线性代数中的线性方程组

最新推荐文章于 2024-09-02 21:41:13 发布

大星小辰

最新推荐文章于 2024-09-02 21:41:13 发布

阅读量2.9k

点赞数 2

分类专栏：线性代数文章标签：线性代数

本文链接：https://blog.csdn.net/qq_28306361/article/details/50787923

版权

线性代数专栏收录该内容

9 篇文章

订阅专栏

还是从解方程组说起
一些概念:
把方程组的系数写成矩阵的形式，称为系数矩阵
把系数矩阵右边添上方程组右边的常数列称为增广矩阵
方程组有解称它相容，否则不相容
若一个矩阵可以经一系列行变换变成另一个矩阵，称两个矩阵行等价

我们在解方程的时候，进行行变换，即倍加、倍乘、对换变换，注意，这三种变换都是可逆的

对应主元列的变量称为基本变量，其他变量称为自由变量
线性方程组相容的重要条件是增广矩阵的最右列不是主元列，就是说，增广矩阵的阶梯形化简后没有形如描述的行，若线性方程组相容，则它的解集
（1）当没有自由变量时，有唯一解
（2）若至少有一个自由变量，有无穷多解。
因为不可能存在这种情况，故此时方程组不相容，若没有自由变量，则这里写图片描述为定值，有唯一解，若有自由变量，如这里写图片描述，自然就有无穷多解

矩阵方程 $这里写图片描述$ 的理解
矩阵方程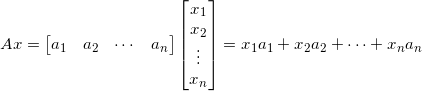
从形式上看，我们知道 $这里写图片描述$ 就是A的各列以x对应元素为权的线性组合，注意Ax仅当A的列数等于x中元素个数时才有定义！
例如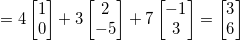 $这里写图片描述$
因此我们有以下定理
$这里写图片描述$ 有解当且仅当b是A的各列的线性组合
齐次方程 $这里写图片描述$ 有非平凡解，当且仅当方程至少有一个自由变量
齐次方程 $这里写图片描述$ 仅有平凡解，当且仅当矩阵A的各列线性无关

线性相关集中不一定每一个向量都是其他向量的线性组合！
若一个向量组的向量个数超过每个向量元素个数，那么这个向量组线性相关
若一个向量组包含零向量，则它线性相关

线性变换 $这里写图片描述$
例如对于一个纵坐标不变，横坐标变为原来k倍的拉伸变换，它的变换矩阵为 $这里写图片描述$
对于一个逆时针旋转一定角度的旋转变换，它的变换矩阵为 $这里写图片描述$
这些变换矩阵的规律是什么？我们可以这样看，对于二维情况，在上述拉伸变换中， $1 0$ 变换为 $k 0$ ，而 $0 1$ 变换为 $0 1$ ，在旋转变换中， $1 0$ 变换为 $这里写图片描述$ ，而 $0 1$ 则变为 $这里写图片描述$ ，不知大家看出来了没有，这个就是最基本的规律，对于复杂的变换，只要弄清楚了 $这里写图片描述$ 等向量变换后的坐标，我们可以直接写出变换矩阵！