Variational Inference with Normalizing Flows翻译

摘要

近似后验分布的选择是变分推断的核心问题之一。大多数变分推断的应用仅采用简单的后验近似，以便高效推理，例如平均场近似或其他简单结构化近似。该限制对使用变分法得到的推理质量具有重大影响。我们引入了一种新方法，用于近似灵活的，任意复杂的和可扩展的后验分布。我们的近似分布是通过一个normalizing flow来构建的分布，从而通过应用一系列可逆变换来将简单的初始分布转化为更复杂的分布，直到达到所需的复杂水平。我们使用normalizing flow的视角来开发有限和无穷小flow的类别，并提供统一的方法来构建丰富的后验近似。我们证明，normalizing flow能更好地匹配真实后验分布，再加上amortized variational方法的可扩展性，可以明显改善变分推断的性能和适用性。

1.介绍

变分推断受到了巨大关注，其作为缩放概率模型在越来越大的数据集上去建模复杂的问题。 现在，变分推理作为大规模文本主题模型的核心，在半监督分类中取得最优结果，这驱动了当前用于生成现实图像的模型的发展，并且是用于许多物理和化学系统的默认工具。尽管变分推断取得了巨大成功和持续的进步，但变分方法的许多缺点限制了它们在更广泛领域和统计推断上应用的能力。后验分布的近似是其限制之一，我们在本文中进行了解决。
　　变分推断要求通过一类已知概率分布近似未知的后验分布，在此期间，我们在其上寻找与真实后验的最佳近似。使用的近似方法通常是有限制的，例如，平均场近似无法地道能够类似于真实后验的分布。这是对变分方法的广泛反对，因为与其他推论方法（例如MCMC）不同，即使在渐近方案中，我们也无法恢复真正的后验分布。
　　有很多证据表明，更丰富，更真实的后验近似确实会导致更好的性能。例如，与利用平均场近似的sigmoid信念网络相比，深度自回归网络使用具有自回归依存结构的后近验似，从而可以明显改善性能。 还有大量证据描述了有限的后验近似带来的有害影响。Turner & Sahani (2011) 提供两种常见问题的展示。首先是后验分布估计不足导致较大方差的问题，基于所选后验近似，这可能会导致较差的预测和不可靠的决策。第二个是后验近似的有限容量也会导致任何模型的MAP估计产生偏差（例如，在时间序列模型中，就是这种情况）。
　　目前已经探索了许多丰富后验近似的方案，通常是基于结构化平均场近似，该近似能够整合近似后验的一些依存形式。另一种潜在的强大替代方案是将后验近似作为混合模型，例如 Jaakkola & Jordan (1998); Jordan et al. (1999); Gershman et al. (2012) 。 但是混合方法限制了变分推断的潜在可扩展性，因为它为了更新每个参数，需要评估每个成分的对数似然和梯度，这通常是计算昂贵的。
　　本文提出了一种新方法，用于近似变分推断的后验分布。我们在第2节中首先回顾当前的通用有向图形模型在变分推断上最优方案，即基于amortized variational inference和efficient Monte Carlo gradient estimation方法。然后我们描述本文的以下贡献：

• 我们提出了使用normalizing flows来近似后验分布，其是一种通过一系列可逆映射对概率密度进行变换来构建复杂分布的工具（第3节）。 normalizing flows的推断提供了更准确的方法，并通过添加具有线性时间复杂度的项来修改变分下界（第4节）。
• 我们表明，normalizing flows允许我们指定一类后验近似，这些近似值能够恢复真正的后验分布，从而克服了一种经常被提到的变分推断限制。
• 我们提出了相关方法的统一视图，以改善后验近似作为一种特殊类型的normalizing flows（第5节）。
• 我们在实验上表明，通用normalizing flows的使用超过了其他进行后验近似的方法。

2.Amortized Variational Inference

为了执行推断，使用概率模型的边缘似然是足够的，并且需要模型中任何缺失或潜在变量的边缘化。这种整合通常是困难的，而且，我们优化了边缘似然的下界。考虑一个通用概率模型，其具有观测值$\text{x}$，必须整合的潜在变量$\text{z}$，以及模型参数$\text{θ}$。我们为潜在变量引入了一个近似后验分布$q_{\varphi }(\text{z}|\text{x})$，并遵循变分原理以获得边缘似然的下界：
$$log{p}_{\theta }(\text{x})=log\int p_{\theta }(\text{x}|\text{z})p(\text{z})d\text{z}\text{\hspace{1em}(1)}$$
$$=log\int \frac{q_{\varphi }(\text{z}|\text{x})}{q_{\varphi }(\text{z}|\text{x})}{p}_{\theta }(\text{x}|\text{z})p(\text{z})d\text{z}\text{\hspace{1em}(2)}$$
$$\ge -{\mathbb{D}}_{KL}[q_{\varphi }(\text{z}|\text{x})||p(\text{z})]+{\mathbb{E}}_q[log{p}_{\theta }(\text{x}|\text{z})]=-\mathcal{F}(\text{x}),\text{\hspace{1em}(3)}$$
其中我们使用了jensen不等式来获得最终的方程，$p_{\theta }(\text{x}|\text{z})$是似然函数，$p(\text{z})$是在潜在变量的先验。我们可以通过参数$\theta$轻松地将该公式扩展到后验推断，但我们将仅关注潜在变量的推断。该公式通常称为负自由能$\mathcal{F}$或置信下界（ELBO）。它由两项组成：首先是近似后验和先验分布（作为正则化发挥作用）的KL散度，第二个是重构误差。该下界(3)提供了一个统一的目标函数，以优化模型的参数$\text{θ}$和$\varphi$。
　　当前最优的变分推断是通过使用mini-batch数据以及随机梯度下降来进行优化执行，这允许将变分推断缩放到非常大的数据集，因此为了能成功使用变分方法，有两个问题必须解决：1）期望对数似然导数$\nabla {\mathbb{E}}_{q_{\varphi }(z)}[log{p}_{\theta }(\text{x}|\text{z})]$的高效计算，2）选择最丰富，计算可行的近似后验分布$q(\cdot )$。 第二个问题是本文的重点。 为了解决第一个问题，我们使用两个工具：蒙特卡洛梯度估计和推理网络，当一起使用时，我们称之为amortized variational inference。

2.1 Stochastic Backpropagation

多年来，变分推断的大部分研究都是在计算期望对数似然的梯度$\nabla {\mathbb{E}}_{q_{\varphi }(z)}[log{p}_{\theta }(\text{x}|\text{z})]$。尽管我们先前可以使用局部变分方法，但是目前我们通常使用蒙特卡洛近似来计算此期望（如果不是已知的，还包括边界中的KL项）。 这种形式被成为双重随机估计，因为我们其中的一个随机源来自于min-batch数据，另一个来自于期望的蒙特卡洛近似。
　　我们专注于具有连续变量的模型，并且我们计算期望梯度的方法是使用具有蒙特卡洛近似的期望重参数化，这被称为随机反向传播，或者随机梯度变分贝叶斯（SGVB）以及仿射变分推断。
　　随机反向传播涉及两个步骤：

• Reparameterization。我们基于一个已知的基本分布和可微分变换（例如局部尺度转换或累积分布函数）来对潜在变量进行重参数化。例如，如果$q_{\varphi }(z)$是高斯分布 N ( z ∣ µ , σ 2 ) , ϕ = { µ , σ 2 } \mathcal N(z|µ,σ^2),\phi=\{µ,σ^2\} N(z∣µ,σ2),ϕ={µ,σ2}，那么使用标准正态分布作为基本分布的局部尺度转换，允许我们能够将$\text{z}$重参数化为：
  $$z\sim \mathcal{N}(z|\mu ,{\sigma }^2)\iff z=\mu +\sigma ϵ,ϵ\sim \mathcal{N}(0,1)$$
• Backpropagation with Monte Carlo。现在，我们使用从基本分布得到的蒙特卡洛近似，来微分（反向传播）变分分布的参数$\varphi$：
  $${\nabla }_{\varphi }{\mathbb{E}}_{q_{\varphi }(z)}[f_{\theta }(z)]\iff {\mathbb{E}}_{\mathcal{N}(ϵ|0,1)}[{\nabla }_{\varphi }{f}_{\theta }(\mu +\sigma ϵ)].$$

基于蒙特卡洛控制变量（MCCV）估计器的许多通用方法是随机反向传播的替代方法，并允许使用可能是连续或离散的潜在变量进行梯度计算。随机反向传播的一个重要优点是，对于具有连续变量的模型，它与其他估计器相比方差最低。

2.2 Inference Networks

第二个重要做法是使用识别模型或推理网络表示近似后验分布$q_{\varphi }(\cdot )$。推理网络是一个模型，该模型可以学习从观测值$x$到潜在变量$z$的逆映射。 使用推理网络，我们可以避免去计算每个数据点的变分参数，而是计算一组全局变分参数$\varphi$。这使我们能够通过推理网络的参数对所有潜在变量的后验估计进行泛化来减少推断成本。我们可以使用的最简单的推理模型是对角高斯密度分布函数$q_{\varphi }(\text{z}|\text{x})=\mathcal{N}(\text{z}|{\text{µ}}_{\varphi }(\text{x}),diag({\text{σ}}_{\varphi }^2(\text{x}))$，其中均值函数${\text{µ}}_{\varphi }(\text{x})$和标准差函数${\text{σ}}_{\varphi }(\text{x})$使用深度神经网络建模。

2.3 Deep Latent Gaussian Models

　　在本文中，我们研究了深度潜在高斯模型（DLGM），它们是一类深度有向图模型，其由$L$层高斯潜在变量${\text{z}}_l$组成。潜在变量的每一层都取决于以上一层的非线性方式，对于DLGM，这种非线性依存是由深度神经网络建模的。联合概率模型为：
$$p(\text{x},{\text{z}}_1,...,{\text{z}}_L)=p(\text{x}|f_0({\text{z}}_1))\prod _{l=1}^{L}p({\text{z}}_l|f_l({\text{z}}_{l+1}))\text{\hspace{1em}(4)}$$
其中第$L$个高斯分布不取决于任何其他随机变量。潜在变量的先验是单位高斯$p({\text{z}}_l)=\mathcal{N}(0,\text{I})$，观测似然$p_{\theta }(\text{x}|\text{z})$则是任何合理的分布，该分布以${\text{z}}_1$为条件，其由深度神经网络参数化（图2）。
　　DLGM使用连续的潜在变量，并且是一种非常适用于使用下界(3)和随机反向传播进行变分推断的模型。DLGM和推理网络的端到端系统可以看作是编码器-编码器架构，该观点由Kingma & Welling (2014) 提出，他们提出将模型和推理策略组合以作为变分自编码器。Kingma & Welling (2014); Rezende et al. (2014) 中使用的推理网络是简单的对角高斯分布。真实的后验分布将比该假设更为复杂，并且使用一种可缩放方法来定义多模式以及约束后验近似仍然是变分推断的一个开放问题。

3.Normalizing Flows

通过检查下界(3)，我们可以看到满足${\mathbb{D}}_{KL}[q||p]=0$最优的变分分布是$q_{\varphi }(\text{z}|\text{x})=p_{\theta }(\text{z}|\text{x})$，即$q$能匹配真实的后验分布。考虑到$q(\cdot )$使用经典分布，例如独立高斯分布或其他平均场近似，这种可能性显然是无法实现的。实际上，由于近似方法的可用选择，变分方法的局限性是，即使在逐渐逼近状态下，我们也无法获得真正的后验分布。 因此，一个理想的变分分布$q_{\varphi }(\text{z}|\text{x})$是高度灵活的，足够灵活以能够包含真正的后验。得到这种理想分布的一条路径是基于normalizing flows的原理。
　　normalizing flow描述了通过一系列可逆映射的概率密度的变换。通过反复应用变量变换规则，初始密度通过可逆映射的序列“流动”。在此变换序列的结尾，我们获得了有效的概率分布，因此这种变换序列称为normalizing flow。

3.1 Finite Flows

概率密度变换的基本规则认为，如果一个平滑映射$f:{\mathbb{R}}^d\to {\mathbb{R}}^d$具有逆变换$f^{-1}=g$，那么有$g\circ f(\text{z})=\text{z}$。如果我们使用此映射将具有分布$q(\text{z})$的随机变量$\text{z}$进行变换，则结果随机变量${\text{z}}^{\prime }=f(\text{z})$具有如下分布：
$$q({\text{z}}^{\prime })=q(\text{z})|det\frac{\partial f^{-1}}{\partial {\text{z}}^{\prime }}|=q(\text{z})|det\frac{\partial f}{\partial \text{z}}{|}^{-1},\text{\hspace{1em}(5)}$$
其中最后一个等式可以看作是链式法则和逆函数的雅可比行列式的应用。我\textbf 们可以通过连续应用（5）组合若干简单映射来构建任意复杂的密度分布。密度分布$q_K(\text{z})$可以通过对具有分布$q_0$的随机变量${\text{z}}_0$进行K次变换$f_k$来获得：
$${\text{z}}_K=f_K\circ ...\circ f_2\circ f_1({\text{z}}_0)\text{\hspace{1em}(6)}$$
$$ln{q}_K({\text{z}}_K)=ln{q}_0({\text{z}}_0)-\sum _{k=1}^{K}lndet|\frac{\partial f_k}{\partial {\text{z}}_k}|,\text{\hspace{1em}(7)}$$
其中方程(6)将在整个论文中作为组合$f_K(f_{K-1}(...f_1(x)))$的缩写。具有初始分布$q_0({\text{z}}_0)$的路径变换${\text{z}}_k=f_k({\text{z}}_{k-1})$被称为flow，由连续分布$q_k$组成的路径形式称为normalizing flow。这种变换的特点，通常称为无意识统计学家法则(Law of the Unconscious Statistician,LOTUS)，其可以在不明确$q_K$情况下可直接计算变换密度$q_K$。任何期望${\mathbb{E}}_{q_K}[h(\text{z})]$都可以写为如下基于$q_0$的期望：
$$E_{q_K}[h(\text{z})]={\mathbb{E}}_{q_o}[h(f_K\circ f_{K-1}\circ ...\circ f_1({\text{z}}_0))],\text{\hspace{1em}(8)}$$
当$h(\text{z})$不依赖于$q_K$时，不需要计算其对数雅可比行列式项。
　　我们可以将可逆流理解为在初始密度上的一系列扩展或收缩影响。对于扩展，映射${\text{z}}^{\prime }=f(\text{z})$将点$\text{z}$从区域${\mathbb{R}}^d$中拉开，从而降低了该区域的密度，同时增加了区域以外的密度。相反，对于收缩，映射将指向区域的内部，同时降低了外部密度，从而增加了内部的密度。
　　现在，normalizing flow这种形式为我们提供了一种系统的方式，可以指定变分推理所需的近似后验分布$q(\text{z}|\text{x})$。通过适当的选择变换$f_K$，我们可以使用一个简单的初始分布，例如独立高斯分布，并应用不同长度的normalizing flow以获得逐渐复杂和多模式的分布。

3.2 Infinitesimal Flows

自然而然地需要考虑一种特殊情况，即normalizing flow的长度趋向于无限。在这种情况下，我们获得了一个infinitesimal flow，其不是用有限的变换序列来描述的，而是描述为初始密度$q_0(\text{z})$随时间演变的偏微分方程：$\frac{\partial }{\partial t}{q}_t(\text{z})={\mathcal{T}}_t[q_t(\text{z})]$，其中$\mathcal{T}$描述了动态连续时间。
　　Langevin Flow。朗之万随机微分方程（SDE）给出了一个重要的flows类别：
$$d\text{z}(t)=\text{F}(\text{z}(t),t)dt+\text{G}(\text{z}(t),t)d\text{ξ}(t),\text{\hspace{1em}(9)}$$
其中$d\text{ξ}(t)$是具有$\mathbb{E}[{\text{ξ}}_i(t)]=0$并且$E[{\text{ξ}}_i(t){\text{ξ}}_j(t^{\prime })]={\delta }_{i,j}\delta (t-t^{\prime })$的维纳过程，$\text{F}$是漂移矢量，$\text{D}=G{G}^T$是扩散矩阵。如果我们通过Langevin flow (9)变换具有初始密度$q_0(\text{z})$的随机变量，那么密度变换的规则由福克-普朗克方程（或概率论中的柯尔莫哥洛夫方程）给出。在时刻$t$时变换的密度$q_t(\text{z})$将演变为：
$$\frac{\partial }{\partial t}{q}_t(\text{z})=-\sum _i\frac{\partial }{\partial z_i}[F_i(\text{z},t)q_t]+\frac{1}{2}\sum _{i,j}\frac{{\partial }^2}{\partial z_i\partial z_j}[D_{ij}(\text{z},t)q_t].$$
　　在机器学习中，我们通常使用$F(\text{z},t)=-{\nabla }_z\mathcal{L}(\text{z})$和$G(\text{z},t)=\sqrt{2}{\delta }_{ij}$的Langevin flow，其中$\mathcal{L}(\text{z})$是我们模型的未归一化对数密度 。
　　重要的是，在这种情况下，$q_t(\text{z})$的固定解由Boltzmann分布给出：$q_{\infty }(\text{z})\propto e^{-\mathcal{L}(\text{z})}$。也就是说，如果我们从初始密度$q_0(\text{z})$开始并通过langevin SDE进化其变量${\text{z}}_0$，则结果变量${\text{z}}_{\infty }$分布将根据$q_{\infty }(z)\propto e^{-\mathcal{L}(\text{z})}$得到，即真实后验分布。Welling & Teh (2011); Ahn et al. (2012); Suykens et al. (1998) 探索了这种方法，用于从复杂密度中抽样。
　　Hamiltonian Flow。还可以用Hamiltonian Monte Carlo方法在一个由动态Hamiltonian $\mathcal{H}(\text{z},\text{ω})=-\mathcal{L}(\text{z})-\frac{1}{2}{\text{ω}}^T\text{M}\text{ω}$得到的增强空间$\tilde{\text{z}}=(\text{z},\text{ω})$上描述normalizing flow。HMC也广泛用于机器学习，例如Neal (2011)。我们将在第5节中使用Hamiltonian flow与Salimans et al. (2015) 中引入的Hamiltonian variational方法建立联系。

4.Inference with Normalizing Flows

为了使用有限normalizing flows进行推断，我们必须指定一个可使用的可逆变换类，以及用于计算雅可比行列式的高效机制。虽然可以直接构建等式（5）中使用的可逆参数化函数，例如可逆神经网络，但这种方法在计算雅可比行列式时非常复杂，复杂度为$O(L{D}^3)$，其中$D$是隐藏维度，$L$是隐藏层的数量。此外，计算雅可比行列式的梯度涉及额外其他操作，这些操作的复杂度也是$O(L{D}^3)$，并且涉及矩阵逆，这些矩阵在数值上是不稳定的。因此，我们要求normalizing flows允许低成本计算行列式或根本不需要雅可比矩阵。

4.1 Invertible Linear-time Transformations

　　我们考虑了如下所示的变换形式：
$$f(\text{z})=\text{z}+\text{u}h({\text{w}}^T\text{z}+b),\text{\hspace{1em}(10)}$$
其中 λ = { w ∈ R D , u ∈ R D , b ∈ R } λ=\{\textbf w∈\mathbb R^D,\textbf u∈\mathbb R^D,b∈\mathbb R\} λ={w∈RD,u∈RD,b∈R}是自由参数，$h(\cdot )$是平滑逐元素非线性变换，其导数为$h^{\prime }(\cdot )$。 对于此映射，我们可以在$O(D)$时间复杂度内计算对数雅可比行列式项：
$$\psi (\text{z})=h^{\prime }({\text{w}}^T\text{z}+b)\text{w}\text{\hspace{1em}(11)}$$
$$det|\frac{\partial f}{\partial \text{z}}|=|det(\text{I}+\text{u}\psi (\text{z}{)}^T)|=|1+{\text{u}}^T\psi (\text{z})|.\text{\hspace{1em}(12)}$$
　　基于等式(7)，我们得出的结论是，通过由等式(10)构建的映射序列$f_k$，能将任意初始分布$q_0(\text{z})$转换得到目标分布$q_K(\text{z})$，且映射序列可简化为：
$$\begin{array}{c}{\text{z}}_K=f_K◦f_{K-1}◦...◦f_1(\text{z})\\ ln{q}_K({\text{z}}_K)=ln{q}_0(\text{z})-{\sum }_{k=1}^{K}ln|1+{\text{u}}_k^T{\psi }_k({\text{z}}_k)|.\end{array}\text{\hspace{1em}(13)}$$
　　由变换(13)定义的flow通过在垂直于超平面$w^T\text{z}+b=0$的方向上应用一系列收缩和扩展来修改初始分布$q_0$，因此我们将这些映射称为planar flow。
　　作为替代方案，我们可以考虑另外一个变换形式，该变换围绕参考点${\text{z}}_0$修改初始密度$q_0$。变换形式是：
$$\begin{array}{c}f(\text{z})=\text{z}+\beta h(\alpha ,r)(\text{z}-{\text{z}}_0),det|\frac{\partial f}{\partial \text{z}}|=[1+\beta h(\alpha ,r){]}^{d-1}[1+\beta h(\alpha ,r)+h^{\prime }(\alpha ,r)r],\end{array},\text{\hspace{1em}(14)}$$
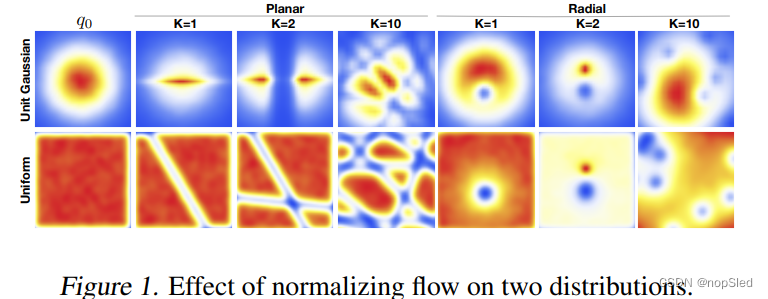
其中$r=|\text{z}-{\text{z}}_0|,h(\alpha ,r)=1/(\alpha +r)$，映射的参数为 λ = { z 0 ∈ R D , α ∈ R , β ∈ R } λ=\{\textbf z_0∈\mathbb R^D,α∈\mathbb R,β∈\mathbb R\} λ={z0​∈RD,α∈R,β∈R}。该变换同样允许行列式的计算是线性的。它围绕参考点应用径向收缩和扩展，因此称为radial flows。我们在图1中显示了两个不同flow在以均匀和高斯为初始分布时收缩和扩展所带来的影响。这种可视化表明，我们可以通过应用两个连续的转换来将球形高斯分布转换为双峰分布。
　　注意到等式(10)或(14)的所有函数都是可逆的。我们在附录中讨论了可逆的条件以及如何以数值稳定的方式满足它们。

4.2 Flow-Based Free Energy Bound

4.3 Algorithm Summary and Complexity

5.Alternative Flow-based Posteriors