Mastering the game of Go with deep neural networks and tree search翻译

摘要

长期以来，围棋游戏一直被认为是人工智能中最具挑战性的游戏，这是由于其巨大的搜索空间以及评估棋盘位置和动作的困难。在这里，我们介绍了一种新的玩围棋的方法，该方法使用“价值网络”来评估棋盘位置，用“策略网络”来选择动作。这些深度神经网络通过从人类专家游戏数据中进行有监督学习，并从self-play游戏中进行强化学习来训练。在没有任何lookahead搜索的情况下，神经网络通过在模拟数千次self-play的最优蒙特卡洛树搜索上玩围棋游戏。我们还引入了一种新的搜索算法，将蒙特卡洛模拟与价值和策略网络相结合。使用此搜索算法，我们的程序AlphaGo与其他GO程序相比，取得了99.8％的胜率，并以5:0的比赛成绩击败了人类的欧洲围棋冠军。

1.介绍

　　所有具有完整信息的游戏都具有最优的价值函数$v^{\ast }(s)$，该​​函数基于棋盘每个位置或状态$s$，能够对游戏的结果进行预测。这类游戏可以通过在一个包含大约$b^d$个可能动作序列的搜索树上，递归计算最优价值函数，其中$b$是游戏的广度（每个位置处合规的动作数），而$d$是其深度（游戏步长）。在大型游戏中，例如国际象棋（$b\approx 35,d\approx 80$），尤其是围棋（$b\approx 250,d\approx 150$），详尽的搜索是不可行的，但是一般可以通过两个原则来缩小有效的搜索空间：
　　首先，可以通过位置评估来减少搜索的深度：在状态$s$处截断搜索树，并将$s$的子树替换为一个近似价值函数$v(s)\approx v^{\ast }(s)$，该函数可预测状态$s$的结果。这种方法在国际象棋，跳棋和奥赛罗上达到了很好的表现，但由于游戏的复杂性，其在围棋中实现很困难。
　　其次，可以通过从策略$p(a|s)$中采样动作来减少搜索的广度，其中$a$是动作的概率分布。例如，通过基于策略$p$采样长动作序列，蒙特卡洛将将搜索到最大深度，而根本不需要分支。
　　对上述两种方式进行平均，能得到一个有效的位置评估，并在十五子棋和拼字游戏上达到非常好的表现，而在围棋游戏中达到业余水平。
　　蒙特卡洛树搜索（MCTS）使用蒙特卡洛采样来估计搜索树中每个状态的价值。随着更多的模拟被执行，搜索树会变得更大，且价值估计变得更加准确。通过选择具有较高价值的子节点，在搜索过程中用于选择动作的策略也随着时间的推移而改善。逐渐地，此策略会收敛到最佳策略，评估也会收敛到最佳价值函数。 当前最强大的围棋程序是基于MCTS的，其通过训练一个预测人类专家动作的策略网络进行增强。这些策略用于将搜索范围缩小到高概率动作（top-K），并在下子过程中采样动作。这种方法取得了强大的业余水平。但是，先前的工作仅限于基于输入特征的线性组合，来得到较简单的策略或价值函数。
　　最近，深度卷积神经网络在视觉领域中取得了前所未有的提升：例如，图像分类，面部识别和玩Atari游戏。他们使用许多在重叠块中排列的神经元层来构建图像中越来越抽象的局部表示。我们为围棋游戏采用了类似的架构。我们以19×19的图像表示棋盘位置，并使用卷积层来构建位置的表示。我们使用这些神经网络来减少搜索树的有效深度和广度，即使用价值网络评估位置，并使用策略网络采样动作。
　　我们使用由若干机器学习阶段组成的管道训练神经网络（图1）。我们首先直接从专业选手的下棋数据中使用有监督学习（SL）训练策略网络$p_{\sigma }$。这提供了快速，有效的学习更新，并具有直接的反馈和高质量的梯度。与先前的工作类似，我们还训练了一个快速策略$p_{\pi }$，可以在下子过程中快速采样动作。接下来，我们训练强化学习（RL）策略网络$p_{\rho }$，通过优化self-play游戏的最终结果来改善SL策略网络。 这可以沿着获得游戏胜利的目标调整策略，而不是最大化预测精度。 最后，我们训练一个价值网络$v_{\theta }$，该网络可以预测由RL策略网络与自身的进行游戏的获胜者。我们的AlphaGo有效地将策略和价值网络与MCTS相结合。

2.策略网络的有监督学习

　　在训练的第一个阶段，我们以先前的工作为基础，通过使用有监督学习以预测围棋游戏中的专家动作。SL策略网络$p_{\sigma }(a|s)$在具有权重$\sigma$和修正非线性的卷积层之间交替forward。最终通过softmax层来输出所有合规动作的概率分布。策略网络的输入$s$是棋盘状态的简化表示（请参见扩展数据表2）。 策略网络在随机采样的状态-动作对$(s,a)$上，使用随机梯度上升进行训练，以最大化在状态$s$时所选择的人类动作$a$的概率：
$$\Delta \sigma \propto \frac{\partial log{p}_{\sigma }(a|s)}{\partial \sigma }$$
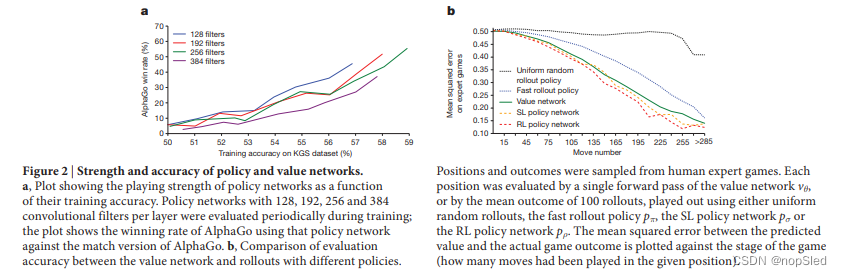
　　我们训练了一个13层策略网络，我们称之为SL策略网络，其数据是从KGS Go Server获取的3000万个棋盘位置。该网络在使用完整输入特征时在测试集上达到57.0%的预测准确率，仅使用棋盘位置和历史动作作为输入时，准确率为55.7%。精度的较小改善能导致了游戏强度的大幅度改善（图2a）。 较大的网络获得更好的准确性，但在搜索过程中评估较慢，因此我们使用具有较少特征的线性softmax网络训练了一个更快但准确较差的快速落子策略$p_{\pi }(a|s)$，尽管精度为24.2%，其选择一个动作仅需2微秒，而不是3毫秒。

3.策略网络的强化学习

在训练的第二阶段，旨在通过策略梯度强化学习（RL）来改善策略网络。RL策略网络$p_{\rho }$与SL策略网络$p_{\sigma }$结构相同，并且其权重$\rho$被初始化为$\rho =\sigma$。我们使用当前的策略网络$p_{\rho }$和迭代训练中随机选择的一个策略网络来玩围棋游戏。通过这种方式从对手池中随机进行，可以防止过度拟合当前策略，从而稳定训练。我们使用一个只有final reward，且中间奖赏为0的奖赏函数$r(s)$，游戏结束时final reward的输出是基于时刻$t$从当前玩家的角度来定义的$z_t=\pm r(s_T)$：如果当前玩家赢，则为1，否则为-1。然后，通过随机梯度上升来最大化期望输出：
$$\Delta \rho \propto \frac{\partial log{p}_{\rho }(a_t|s_t)}{\partial \rho }{z}_t$$
　　我们在游戏中评估了RL策略网络的性能，从输出概率分布上中对动作进行采样$a_t\sim p_{\rho }(\cdot |s_t)$。当以端到端方式对战时，RL策略网络相比SL策略网络赢得了80％以上的游戏。我们还测试了最强的开源围棋程序，Pachi，这是一个复杂的Monte Carlo搜索程序，每次动作选择都执行100,000个模拟。RL策略网络完全不进行搜索，都赢得了85％的游戏。相比之下，先前仅对卷积网络进行有监督学习的模型，赢得了11％的比赛。

4.价值网络的强化学习

训练的最后一个阶段主要关注位置评估，以估计一个价值函数$v^p(s)$，其用来预测由策略$p$执行的在位置$s$处的结果：
$$v^p(s)=\mathbb{E}[z_t|s_t=s,a_{t...T}\sim p]$$
　　理想情况下，我们期望知道最优价值函数$v^{\ast }(s)$以进行完美游戏。实际上，我们使用RL策略网络$p_{\rho }$来估算价值函数$v^{p_{\rho }}$。另外，我们使用一个具有权重$\theta$的价值网络$v_{\theta }(s)$来近似这一函数，则$v_{\theta }(s)\approx v^{p_{\rho }}(s)\approx v^{\ast }(s)$。该神经网络具有与策略网络相似的架构，但是输出单个预测值而不是概率分布。我们在状态-结果对$(s,z)$上以回归的方式训练价值网络的权重，其主要通过以随机梯度下降的方式来最小化预测值$v_{\theta }(s)$和真实结果$z$之间的均方误差（MSE）：
$$\Delta \theta \propto \frac{\partial v_{\theta }(s)}{\partial \theta }(z-v_{\theta }(s))$$
　　从由一个完整游戏构建的数据中训练模型这简单方法会导致过拟合。该问题在于，同一场游戏中两个连续位置是密切相关的，其只有一个棋子不同，但是整盘游戏的回归目标都是共享的。当以这种方式对KGS数据集进行训练时，价值网络仅能记住了该盘游戏的结果，而无法泛化到新的位置，这导致测试集上的最低MSE为0.37，而训练集则为0.19。为了减轻此问题，我们通过self-paly生成了一组新的数据集，该数据集由3000万个不同的位置组成，每个位置都是从一盘单独的游戏中采样的。每盘游戏都是通过RL策略网络机器本身之间进行的，直到游戏终止为止。对该数据集的训练导致训练和测试集的MSE分别为0.226和0.234，这表明过拟合情况减少。图2b展示了使用价值网络进行位置评估的准确性，与使用快速落子策略$p_{\pi }$的蒙特卡罗搜索相比，价值函数能够更加准确。对$v^{\ast }(s)$的评估还可以使用RL策略网络$p_{\rho }$来进行蒙特卡洛搜索，但使用价值网络将使计算量减少15,000倍。

5.使用策略和价值网络搜索

　　AlphaGo在MCTS算法中将策略和价值网络结合在一起（图3），该算法通过lookahead搜索来选择动作。搜索树的每条边$(s,a)$存储了：动作价值$Q(s,a)$，访问次数$N(s,a)$和先验概率$P(s,a)$。从根状态开始，树通过仿真进行来遍历。在仿真的每个时刻$t$，动作$a_t$通过下式从状态$s_t$中进行选择：
$$a_t=\underset{a}{\mathrm{argmax}}(Q(s_t,a)+u(s_t,a))$$
这能为最大化动作价值添加一个探索：
$$u(s,a)\propto \frac{P(s,a)}{1+N(s,a)}$$
其与先验概率成正比，并随着访问次数的增加而减少，以鼓励探索。当遍历在步骤$L$处到达叶子节点$s_L$时，该叶子节点可以被扩展。此时，叶子位置$s_L$由策略网络$p_{\sigma }$ forward一次，其输出概率作为每个合规动作$a$的先验概率$P$被存储$P(s,a)=p_{\sigma }(a|s)$。叶子节点以两种截然不同的方式进行评估：首先由价值网络$v_{\theta }(s_L)$评估，其次，通过快速落子策略$p_{\pi }$下到终止步骤$T$来得到结果$z_L$，然后使用混合参数$\lambda$将这些评估合并为叶子评估$V(s_L)$：
$$V(s_L)=(1-\lambda )v_{\theta }(s_L)+\lambda z_L$$
　　在仿真结束时，所有被遍历过边的动作价值和访问次数将更新。每个边都累积了访问次数，并用其平均通过该边的所有价值：
$$\begin{array}{c}N(s,a)={\sum }_{i=1}^{n}1(s,a,i)\\ Q(s,a)=\frac{1}{N(s,a)}{\sum }_{i=1}^{n}1(s,a,i)V(s_L^i)\end{array}$$
其中$s_L^i$是第$i$次仿真的叶子节点，而$1(s,a,i)$表示在第$i$次仿真过程中是否遍历过改条边。搜索完成后，该算法选择访问量最多的动作。
　　值得注意的是，SL策略网络在AlphaGo中的性能要比更强的RL策略网络$p_{\rho }$表现更好，这大概是因为人类选择了有希望动作的多样化beam，而RL优化了单一的最佳动作。但是，从较强的RL策略网络中得出的价值$v_{\theta }(s)\approx v^{p_p}(s)$比源自SL策略网络得出的价值值$v_{\theta }(s)\approx v^{p_{\sigma }}(s)$更好。
　　评估策略和价值网络需要比传统启发式搜索方法多几个数量级计算。为了有效地将MCTS与深度神经网络相结合，AlphaGo使用异步的多线程搜索，该搜索在CPU上执行仿真，并在GPU上并行计算策略和价值网络。AlphaGo的最终版本使用了40个搜索线程，48个CPU和8 GPU。我们还实现了AlphaGo的分布式版本，该版本利用了多台机器，40个搜索线程，1,202个CPU和176 GPU。Methods部分提供了异步和分布式MCTS的完整详细信息。

方法

Problem setting

Prior work

Search algorithm

为了高效地将大型神经网络整合到AlphaGo中，我们实现了异步策略和价值MCTS算法（APV-MCTS）。搜索树中的每个节点$s$都包含了所有合规动作$a\in \mathcal{A}(s)$的边$(s,a)$。每个边存储一组统计信息：
{ P ( s , a ) , N v ( s , a ) , N r ( s , a ) , W v ( s , a ) , W r ( s , a ) , Q ( s , a ) } \{P(s,a),N_v(s,a),N_r(s,a),W_v(s,a),W_r(s,a),Q(s,a)\} {P(s,a),Nv​(s,a),Nr​(s,a),Wv​(s,a),Wr​(s,a),Q(s,a)}
其中$P(s,a)$是先验概率，$W_v(s,a)$和$W_r(s,a)$是蒙特卡洛的总动作价值估计，$N_v(s,a)$和$N_r(s,a)$是累积访问次数，下标$v$和$r$分别是叶子结点上网络的价值估计和落子策略的价值估计。多个仿真在单独的搜索线程上并行执行。在图3中概述了APV-MCTS算法的四个阶段。
　　Selection (Fig. 3a)。每次仿真开始于搜索树的根部，并在时刻$L$到达叶子节点时结束。在每个时刻$t<L$，基于搜索树内的统计结果来选择一个动作，$a_t=argma{x}_a(Q(s_t,a),u(s_t,a))$，这使用PUCT算法的变种，其中$u(s,a)=c_{puct}P(s,a)\frac{\sqrt{{\sum }_b{N}_r(s,b)}}{1+N_r(S,A)}$且$c_{puct}$是一个常数，用来决定探索率。这种搜索控制策略在初始时倾向于具有高先验概率低访问率的动作，但会逐渐倾向于具有高动作价值的动作。
　　Evaluation (Fig. 3c)。除非叶子结点先前已被评估过，否则将该叶子结点$s_L$添加到队列中以通过价值网络评估$v_{\theta }(s_L)$。每次仿真的落子阶段开始于叶子节点$s_L$，一直持续到游戏结束。在这些时刻$t\ge L$中，每个玩家都根据落子策略$a_t\sim p_{\pi }(\cdot |s_t)$选择动作。当游戏达到终止状态时，结果$z_t=\pm r(s_T)$将从最终分数计算。
　　Backup (Fig. 3d)。在仿真的每个树中步骤$t\le L$上，当落子策略执行的失败次数到达$n_{vl}$，落子的统计信息被更新，$N_r(s_t,a_t)\leftarrow N_r(s_t,a_t)+n_{vl};W_r(s_t,a_t)\leftarrow W_r(s_t,a_t)-n_{vl}$，这种虚拟损失阻止其他线程同时探索相同的路径。在仿真结束时，通过在每个步骤$t\le L$上反向传播来更新落子统计信息，以替换虚拟损失，$N_r(s_t,a_t)\leftarrow N_r(s_t,a_t)-n_{vl}+1;W_r(s_t,a_t)\leftarrow W_r(s_t,a_t)+n_{vl}+z_t$。异步地，当对叶子结点$s_L$的评估完成时，将启动单独的反向传播。价值网络$v_{\theta }(s_L)$的输出用于在第二个反向传播过程更新每个步骤$t\le L$中的统计值$N_v(s_t,a_t)\leftarrow N_v(s_t,a_t)+1;W_r(s_t,a_t)\leftarrow W_r(s_t,a_t)+v_{\theta }(s_L)$。每个状态动作的最终评估是蒙特卡洛估计值的加权平均，$Q(s,a)=(1-\lambda )\frac{W_v(s,a)}{N_v(s,a)}+\lambda \frac{W_r(s,a)}{N_r(s,a)}$。所有的线程更新均无锁执行。
　　Expansion (Fig. 3b)（动态扩展）。当落子策略的访问次数超过指定阈值时，即$N_r(s,a)>n_{thr}$，一个新的状态结点$s^{\prime }=f(s,a)$被添加到搜索树中，且新节点初始化为 { N v ( s ′ , a ) = N r ( s ′ , a ) = 0 , W v ( s ′ , a ) = W r ( s ′ , a ) = 0 , P ( s ′ , a ) = p σ ( a ∣ s ′ ) } \{N_v(s',a)=N_r(s',a)=0,W_v(s',a)=W_r(s',a)= 0,P(s',a)=p_σ(a|s')\} {Nv​(s′,a)=Nr​(s′,a)=0,Wv​(s′,a)=Wr​(s′,a)=0,P(s′,a)=pσ​(a∣s′)}，先验概率首先被一个树策略$p_{\tau }(a|s^{\prime })$（这类似与落子策略，但是具有更多特征）初始化。然后，位置$s^{\prime }$被插入队列，以在GPU策略网络上异步评估，其先验概率使用具有参数$\beta$为temperature的softmax输出$p_{\sigma }^{\beta }(\cdot |s^{\prime })$，并使用原子更新将其替换原始先验概率$P(s^{\prime },a)\leftarrow p_{\sigma }^{\beta }(a|s^{\prime })$。另外，阈值$n_{thr}$被动态调整，以确保将位置添加到策略队列中的速率与GPU评估策略网络的速率匹配。
　　我们还实现了分布式APV-MCTS算法。该结构主要由单个主机执行搜索，许多远程Worker CPU执行异步落子，以及许多Worker GPU执行异步策略和价值网络评估。整个搜索树都存储在主机上，该树仅执行每次仿真的树内阶段。将叶子位置传达给worder CPU，后者执行仿真的落子阶段，并向Worker GPU传达，用来阶段评估策略和价值网络。策略网络的先验概率返回给主机，在那里用于替换新扩展的节点上的先验概率。从落子和价值网络输出的奖赏分别返回到主机，并备份原始搜索路径。
　　在搜索结束时，AlphaGo以最大访问次数而不是最大动作价值选择动作，这对离群值不太敏感。 在随后的时刻中重复使用搜索树：与执行动作相对应的子节点成为新的根节点；该结点下方的子树及其所有统计数据都保留，而树的其余部分则被丢弃。

Rollout policy

Symmetries

Policy network

Value network

Features for policy/value network

Neural network architecture

Evaluation