LibSVM支持向量回归详解

LibSVM是是台湾林智仁(Chih-Jen Lin)教授2001年开发的一套支持向量机的库，可以很方便的对数据做分类或回归。由于LibSVM程序小，运用灵活，输入参数少，并且是开源的，易于扩展，因此成为目前国内应用最多的SVM的库，同时sklearn.svm也是使用的该库。

网络上对于LibSVM源码的讲解有很多，但个人感觉绝大多数讲解的不够清晰，很多都是贴个理论公式图片再粘段代码就一带而过。并且网络上基本都是对SVC的讲解，SVR部分几乎没有提及（虽然SVR只是SVC的扩展）。因此本篇博文将系统地讲解LibSVM中SVR训练与预测部分的源码（想学习SVC的同学同样适用）。

python复现LIBSVM中SVR部分功能可参见 https://github.com/KunBB/LibSVM_SVR_python

LibSVM整体流程

train：

//根据svm_type的不同进行初始化
svm_train()
    //根据svm_type的不同调用不同的分类回归训练函数
    svm_train_one()
        //针对epsilon-SVR这一类型进行模型参数初始化
        solve_epsilon_svr()
            //使用SMO算法求解对偶问题（二次优化问题）
            Solver::Solve()
                    //每隔若干次迭代进行一次shrinking，对样本集进行缩减降低计算成本
                    Solver::do_shrinking()
                    //若满足停止条件则进行梯度重建并跳出循环
                    Solver::reconstruct_gradient()
                    //选择出当前最大违反对i,j
                    Solver::select_working_set()
                //计算参数优化后的rho
                Solver::caculate_rho()
            //得到优化后的alpha和SolutionInfo对象si
        //得到优化后的alpha和SolutionInfo对象si
    //得到decision_function对象f
//得到svm_model对象model

predict

//根据svm_type的不同开辟dec_value空间
svm_predict()
    //根据svm_type的不同调用k_function函数
    svm_predict_values()
        //根据kernel_type的不同计算k(i,j)
        Kernel::k_function()
        //得到k(x_train[i],x_test[j])
    //得到预测值y_pre[j]
//得到预测值y_pre[j]

---

svm.h文件解析

svm_node

//存储一个样本（假设为样本i）的一个特征
struct svm_node{
    int index;   //样本i的特征索引值，最后一个为-1
    double value;   //样本i第index个特征的值，最后一个为NULL
};

如：x[i]={0.23,1.2,3.5,1.5}
则需使用五个svm_node来表示x[i]，具体映射如下：

index	0	1	2	3	-1
value	0.23	1.2	3.5	1.5	NULL

svm_problem

//存储参加运算的所有样本数据（训练集）
struct svm_problem{
        int l;    //样本总数
        double *y;    //样本输出值（所属类别）
        struct svm_node **x;    //样本输入值
};

下图中最右边的长条格同上表，存储了三维数据。

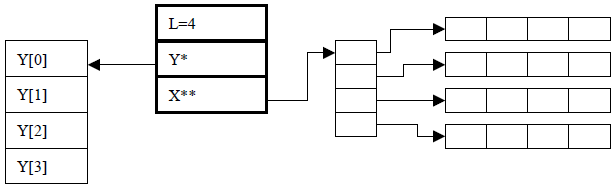
**svm_problem中的y与类Solver中的y并不完全一样!!!**对于一般SVC而言可以看出一样的，其值为-1与+1，对于多分类而言svm_problem.y[i]可以是1、2、3等，而多类计算其实是二分类的组合，因此在二分类中y[i]依然等于+1与-1.更特殊的，在SVR中，svm_problem的y[i]等于其目标值，如：11.234、56.24、5.23等，在计算时svm_problem.y[i]整合到了Solver.p[i]与Solver.p[i+svm_problem.l]中（具体的问题后续章节再详细解释），而在Solver.y[i]依然为+1和-1.

svm_parameter

//svm_type和svm_type可能取值
enum { C\_SVC, NU\_SVC, ONE\_CLASS, EPSILON\_SVR, NU\_SVR };/* svm_type */
enum { LINEAR, POLY, RBF, SIGMOID }; /* kernel_type */

//svm模型训练参数
struct svm_parameter
    {
        int svm_type;
        int kernel_type;
        int degree; /* for poly */
        double gamma;   /* for poly/rbf/sigmoid */
        double coef0;   /* for poly/sigmoid */

        /* these are for training only */
        double cache_size; /* in MB */
        double eps; /* stopping criteria */
        double C;   /* for C_SVC, EPSILON_SVR and NU_SVR */
        int nr_weight;      /* for C_SVC */
        int *weight_label;  /* for C_SVC */
        double* weight;     /* for C_SVC */
        double nu;  /* for NU_SVC, ONE_CLASS, and NU_SVR */
        double p;   /* for EPSILON_SVR */
        int shrinking;  /* use the shrinking heuristics */
        int probability; /* do probability estimates */
    };

LibSVM中的核函数如下：

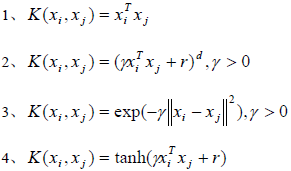
各参数解释如下：

Parameter	Interpretation
degree	2式中的d
gamma	2,3,4式中的gamma
coef0	2,4式中的r
cache_size	单位MB，训练所需内存，LibSVM2.5默认4M
eps	停止条件需满足的最大误差值(文献[2]中式3.9)
C	惩罚因子，越大模型过拟合越严重
nr_weight	权重的数目,目前在实例代码中只有两个值，一个是默认0，另外一个是svm_binary_svc_probability函数中使用数值2
*weight_label	权重，元素个数由nr_weight决定.
nu	NU_SVC,ONE_CLASS,NU_SVR中的nu
p	SVR中的间隔带epsilon
shrinking	指明训练过程是否使用压缩
probability	指明是否做概率估计

svm_model

//保存训练后的模型参数
struct svm_model{
        struct svm_parameter param; /* parameter */
        int nr_class;       /* number of classes, = 2 in regression/one class svm */
        int l;          /* total #SV */
        struct svm_node **SV;       /* SVs (SV[l]) */
        double **sv_coef;   /* coefficients for SVs in decision functions (sv_coef[k-1][l]) */
        double *rho;        /* constants in decision functions (rho[k*(k-1)/2]) */
        double *probA;      /* pariwise probability information */
        double *probB;
        int *sv_indices;        /* sv_indices[0,...,nSV-1] are values in [1,...,num_traning_data] to indicate SVs in the training set */

                                /* for classification only */

        int *label;     /* label of each class (label[k]) */
        int *nSV;       /* number of SVs for each class (nSV[k]) */
                        /* nSV[0] + nSV[1] + ... + nSV[k-1] = l */
                        /* XXX */
        int free_sv;        /* 1 if svm_model is created by svm_load_model*/
                            /* 0 if svm_model is created by svm_train */
};

各参数解释如下：

Parameter	Interpretation
param	训练参数
nr_class	类别数
l	支持向量数
**SV	作为支持向量的样本集
**sv_coef	支持向量系数alpha
*rho	判别函数中的b
*proA	成对概率信息
*proB	成对概率信息
*sv_indices	记录支持向量在训练数据中的index
*label	各类的标签
*nSV	各类的支持向量数
free_SV	若model由svm_load_model函数生成则为1，若为svm_train生成则为0

---

svm.cpp文件解析

下图为svm.cpp中的类继承和组合情况（实现表示继承关系，虚线表示组合关系）：

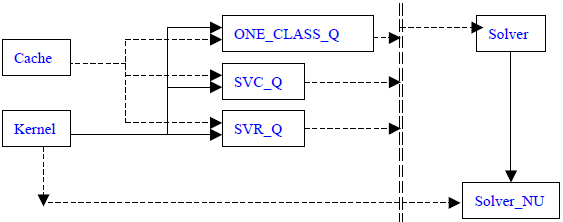
Cache类主要负责运算所涉及的内存的管理，包括申请、释放等。本篇博文主要讲解SVM求解过程，对于Cache类将不予解析。

Kernel类

class Kernel : public QMatrix {
public:
    Kernel(int l, svm_node * const * x, const svm_parameter& param);
    virtual ~Kernel();

    static double k_function(const svm_node *x, const svm_node *y,
        const svm_parameter& param);
    virtual Qfloat *get_Q(int column, int len) const = 0;
    virtual double *get_QD() const = 0;
    virtual void swap_index(int i, int j) const // no so const...
    {
        swap(x[i], x[j]);
        if (x_square) swap(x_square[i], x_square[j]);
    }
protected:

    double (Kernel::*kernel_function)(int i, int j) const;

private:
    const svm_node **x;
    double *x_square;

    // svm_parameter
    const int kernel_type;
    const int degree;
    const double gamma;
    const double coef0;

    static double dot(const svm_node *px, const svm_node *py);
    double kernel_linear(int i, int j) const
    {
        return dot(x[i], x[j]);
    }
    double kernel_poly(int i, int j) const
    {
        return powi(gamma*dot(x[i], x[j]) + coef0, degree);
    }
    double kernel_rbf(int i, int j) const
    {
        return exp(-gamma * (x_square[i] + x_square[j] - 2 * dot(x[i], x[j])));
    }
    double kernel_sigmoid(int i, int j) const
    {
        return tanh(gamma*dot(x[i], x[j]) + coef0);
    }
    double kernel_precomputed(int i, int j) const
    {
        return x[i][(int)(x[j][0].value)].value;
    }
};

成员变量

Parameter	Interpretation
svm_node **x	训练样本数据
*x_square	x[i]^T*x[i]，使用RBF核会用到
kernel_type	核函数类型
degree	svm_parameter
gamma	svm_parameter
coef0	svm_parameter

成员函数

Kernel(int l, svm_node * const * x, const svm_parameter& param);

构造函数。初始化类中的部分常量、指定核函数、克隆样本数据。

Kernel::Kernel(int l, svm_node * const * x_, const svm_parameter& param)
    :kernel_type(param.kernel_type), degree(param.degree),
    gamma(param.gamma), coef0(param.coef0)
{
    switch (kernel_type)    //根据kernel_type的不同定义相应的函数kernel_function()
    {
    case LINEAR:
        kernel_function = &Kernel::kernel_linear;
        break;
    case POLY:
        kernel_function = &Kernel::kernel_poly;
        break;
    case RBF:
        kernel_function = &Kernel::kernel_rbf;
        break;
    case SIGMOID:
        kernel_function = &Kernel::kernel_sigmoid;
        break;
    case PRECOMPUTED:
        kernel_function = &Kernel::kernel_precomputed;
        break;
    }

    clone(x, x_, l);

    if (kernel_type == RBF)    //如果使用RBF 核函数，则计算x_sqare[i]，即x[i]^T*x[i]
    {
        x_square = new double[l];
        for (int i = 0; i<l; i++)
            x_square[i] = dot(x[i], x[i]);
    }
    else
        x_square = 0;
}

static double dot(const svm_node *px, const svm_node *py);

点乘函数，点乘两个样本数据，按svm_node 中index (一般为特征)进行运算，一般来说，index为1，2，…直到-1。返回点乘总和。例如：x1={1,2,3} ,x2={4,5,6}总和为sum=1*4+2*5+3*6;在svm_node[3]中存储index=-1时，停止计算。

double Kernel::dot(const svm_node *px, const svm_node *py)
{
    double sum = 0;
    while (px->index != -1 && py->index != -1)
    {
        if (px->index == py->index)
        {
            sum += px->value * py->value;
            ++px;
            ++py;
        }
        else
        {
            if (px->index > py->index)
                ++py;
            else
                ++px;
        }
    }
    return sum;
}

static double k_function(const svm_node *x, const svm_node *y, const svm_parameter& param);

功能类似kernel_function,不过kerel_function用于训练，k_function用于预测。

double Kernel::k_function(const svm_node *x, const svm_node *y,
    const svm_parameter& param)    //输入数据为两个数据样本，其中一个为训练样本一个为测试样本
{
    switch (param.kernel_type)
    {
    case LINEAR:
        return dot(x, y);
    case POLY:
        return powi(param.gamma*dot(x, y) + param.coef0, param.degree);
    case RBF:
    {
        double sum = 0;
        while (x->index != -1 && y->index != -1)
        {
            if (x->index == y->index)
            {
                double d = x->value - y->value;
                sum += d * d;
                ++x;
                ++y;
            }
            else
            {
                if (x->index > y->index)
                {
                    sum += y->value * y->value;
                    ++y;
                }
                else
                {
                    sum += x->value * x->value;
                    ++x;
                }
            }
        }

        while (x->index != -1)
        {
            sum += x->value * x->value;
            ++x;
        }

        while (y->index != -1)
        {
            sum += y->value * y->value;
            ++y;
        }

        return exp(-param.gamma*sum);
    }
    case SIGMOID:
        return tanh(param.gamma*dot(x, y) + param.coef0);
    case PRECOMPUTED:  //x: test (validation), y: SV
        return x[(int)(y->value)].value;
    default:
        return 0;  // Unreachable
    }
}

其中RBF部分很有讲究。因为存储时，0值不保留。如果所有0值都保留，第一个while就可以都做完了；如果第一个while做不完，在x，y中任意一个出现index＝-1，第一个while就停止，剩下的代码中两个while只会有一个工作，该循环直接把剩下的计算做完。

virtual Qfloat *get_Q(int column, int len);

纯虚函数，将来在子类中实现(如class SVR_Q)，计算Q值。相当重要的函数。

virtual Qfloat *get_Q(int column, int len) const = 0;

virtual void swap_index(int i, int j);

虚函数，x[i]和x[j]中所存储指针的内容。如果x_square不为空，则交换相应的内容。

virtual void swap_index(int i, int j) const // no so const...
    {
        swap(x[i], x[j]);
        if (x_square) swap(x_square[i], x_square[j]);
    }

virtual double *get_QD();

纯虚函数，将来在子类中实现(如class SVR_Q),计算Q[i,i]值。

virtual Qfloat *get_Q(int column, int len) const = 0;

double (Kernel::*kernel_function)(int i, int j)；

函数指针，根据相应的核函数类型，来决定所使用的函数。在计算矩阵Q时使用。

double (Kernel::*kernel_function)(int i, int j) const;

Solver类

class Solver {
public:
    Solver() {};
    virtual ~Solver() {};

    struct SolutionInfo {
        double obj;
        double rho;
        double upper_bound_p;
        double upper_bound_n;
        double r;   // for Solver_NU
    };

    void Solve(int l, const QMatrix& Q, const double *p_, const schar *y_,
        double *alpha_, double Cp, double Cn, double eps,
        SolutionInfo* si, int shrinking);
protected:
    int active_size;
    schar *y;
    double *G;      // gradient of objective function
    enum { LOWER_BOUND, UPPER_BOUND, FREE };
    char *alpha_status; // LOWER_BOUND, UPPER_BOUND, FREE
    double *alpha;
    const QMatrix *Q;
    const double *QD;
    double eps;
    double Cp, Cn;
    double *p;
    int *active_set;
    double *G_bar;      // gradient, if we treat free variables as 0
    int l;
    bool unshrink;  // XXX

    double get_C(int i)
    {
        return (y[i] > 0) ? Cp : Cn;
    }
    void update_alpha_status(int i)
    {
        if (alpha[i] >= get_C(i))
            alpha_status[i] = UPPER_BOUND;
        else if (alpha[i] <= 0)
            alpha_status[i] = LOWER_BOUND;
        else alpha_status[i] = FREE;
    }
    bool is_upper_bound(int i) { return alpha_status[i] == UPPER_BOUND; }
    bool is_lower_bound(int i) { return alpha_status[i] == LOWER_BOUND; }
    bool is_free(int i) { return alpha_status[i] == FREE; }
    void swap_index(int i, int j);
    void reconstruct_gradient();
    virtual int select_working_set(int &i, int &j);
    virtual double calculate_rho();
    virtual void do_shrinking();
private:
    bool be_shrunk(int i, double Gmax1, double Gmax2);
};

成员变量

结构体SolutionInfo为求解优化中的参数信息。

各参数解释如下：

Parameter	Interpretation
SolutionInfo.obj	求解优化过程中的目标函数值
SolutionInfo.rho	判别函数中的b
SolutionInfo.upper_bound_p	对于不平衡数据集，该值对应惩罚因子Cp
SolutionInfo.upper_bound_n	对于不平衡数据集，该值对应惩罚因子Cn
SolutionInfo.r	用于Solver_NU
active_size	计算时实际参加运算的样本数目，经过shrink处理后，该数目会小于全部样本总数。
*y	样本所属类别，该值只取+1/-1 。虽然可以处理多类，最终是用两类SVM 完成的。
*G	梯度G=Qα+P
*alpha_status	α[i]的状态，根据情况分为α[i]≤0,α[i]≥c和0<α[i]<\c,分别对应内部点(非SV)，错分点(BSV)和支持向量(SV)。
*alpha	α[i]
*Q	对应公式中Q的某一列
*QD	对应公式中的Q[i][i]
eps	停止条件的误差限
Cp，Cn	对应不平衡数据的惩罚因子，若不为不平数据或是对于SVR来说Cp=Cn=C
*p	对应梯度公式中的p，即SVR中的间隔带epsilon
*active_set	active对应的index
*G_bar	sum(C*Q)
l	数据样本个数
unshrink	是否被压缩

成员函数

double get_C(int i)；

返回对应于样本的C。设置不同的Cp 和Cn 是为了处理数据的不平衡。见[1]中的Unbalanced data.对于一般样本数据Cp=Cn。

double get_C(int i)
    {
        return (y[i] > 0) ? Cp : Cn;
    }

void swap_index(int i, int j);

完全交换样本i和样本j的内容，包括所申请的内存的地址。

void Solver::swap_index(int i, int j)
{
    Q->swap_index(i, j);
    swap(y[i], y[j]);
    swap(G[i], G[j]);
    swap(alpha_status[i], alpha_status[j]);
    swap(alpha[i], alpha[j]);
    swap(p[i], p[j]);
    swap(active_set[i], active_set[j]);
    swap(G_bar[i], G_bar[j]);
}

template <class T> static inline void swap(T& x, T& y) { T t = x; x = y; y = t; }

void reconstruct_gradient();

重新计算梯度。

void Solver::reconstruct_gradient()
{
    // reconstruct inactive elements of G from G_bar and free variables

    if (active_size == l) return;

    int i, j;
    int nr_free = 0;

    for (j = active_size; j<l; j++)
        G[j] = G_bar[j] + p[j];

    for (j = 0; j<active_size; j++)
        if (is_free(j))
            nr_free++;

    if (2 * nr_free < active_size)
        info("\nWARNING: using -h 0 may be faster\n");

    if (nr_free*l > 2 * active_size*(l - active_size))
    {
        for (i = active_size; i<l; i++)
        {
            const Qfloat *Q_i = Q->get_Q(i, active_size);
            for (j = 0; j<active_size; j++)
                if (is_free(j))
                    G[i] += alpha[j] * Q_i[j];
        }
    }
    else
    {
        for (i = 0; i<active_size; i++)
            if (is_free(i))
            {
                const Qfloat *Q_i = Q->get_Q(i, l);
                double alpha_i = alpha[i];
                for (j = active_size; j<l; j++)
                    G[j] += alpha_i * Q_i[j];
            }
    }
}

G_bar[i]在初始化时并未加入p[i]，所以程序首先增加p[i]。Shrink后依然参加运算的样本位于active_size和l-1位置上。在0～active_size之间的alpha[i]如果在区间(0,c)上，才有必要更新相应的active_size和l-1位置上的样本的梯度。

virtual void do_shrinking();

对样本集做缩减。当0<α<C时(还有两种情况),程序认为该样本可以不参加下次迭代。(0<α<C时，为内部点)程序会减小active_size，为内部点增加位置。active_size表明了不可以参加下次迭代的样本的最小标签号，在active_size与l之间的元素都对分类没有贡献。

void Solver::do_shrinking()
{
    int i;
    double Gmax1 = -INF;        // max { -y_i * grad(f)_i | i in I_up(\alpha) }
    double Gmax2 = -INF;        // max { y_i * grad(f)_i | i in I_low(\alpha) }

                                // find maximal violating pair first
    for (i = 0; i<active_size; i++)
    {
        if (y[i] == +1)
        {
            if (!is_upper_bound(i))    // < C
            {
                if (-G[i] >= Gmax1)
                    Gmax1 = -G[i];
            }
            if (!is_lower_bound(i))
            {
                if (G[i] >= Gmax2)
                    Gmax2 = G[i];
            }
        }
        else
        {
            if (!is_upper_bound(i))
            {
                if (-G[i] >= Gmax2)
                    Gmax2 = -G[i];
            }
            if (!is_lower_bound(i))
            {
                if (G[i] >= Gmax1)
                    Gmax1 = G[i];
            }
        }
    }
    //如果程序在缩减一次后没有达到结束条件，就重新构造梯度矢量，并再缩减一次。
    if (unshrink == false && Gmax1 + Gmax2 <= eps * 10)
    {
        unshrink = true;
        reconstruct_gradient();
        active_size = l;
        info("*");
    }
    //程序中active_size--是为了消除交换后的影响，使重新换来的样本也被检查一次。
    for (i = 0; i<active_size; i++)
        if (be_shrunk(i, Gmax1, Gmax2))
        {
            active_size--;
            while (active_size > i)
            {
                if (!be_shrunk(active_size, Gmax1, Gmax2))
                {
                    swap_index(i, active_size);
                    break;
                }
                active_size--;
            }
        }
}

virtual int select_working_set(int &i, int &j);

该函数求解出违反KKT条件最严重的目标对i与j。
我们先来了解一下working set的选择原理。参考文献[3]。

选择i

SVM的对偶问题为：

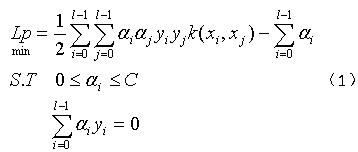
SVM收敛的充分必要条件(KKT条件)为：

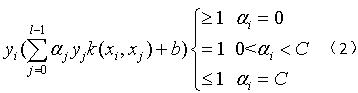
对(1)式求导可以得到：

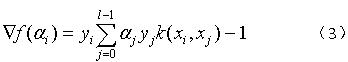
①yi=1，αi<C，由(2)和(3)可得：

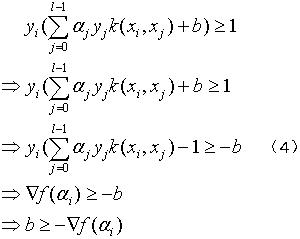
②yi=-1，αi>0，由(2)和(3)可得：

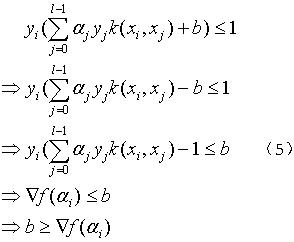
③yi=-1，αi<C，由(2)和(3)可得：

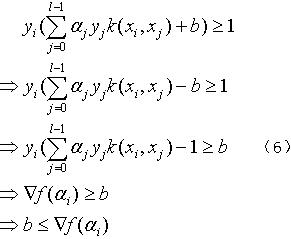
④yi=1，αi>0，由(2)和(3)可得：

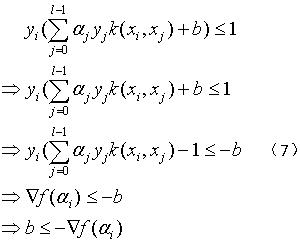
对式(4)、(5)、(6)、(7)进行约简得到式(8):

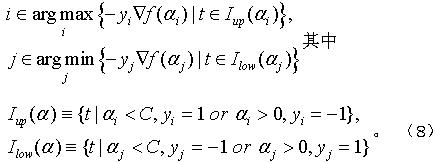
可以发现，(4)和(5)都是b大于某个数，(6)和(7)都是b小于某个数。因为b是个常量，那么根据上述条件，我们可以得到以下结论，在合理的αi和αj下，有：

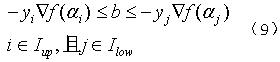
我们就是要从中挑选违反上述条件的αi和αj，来进行重新的迭代和更新，使得所有的αi和αj都满足上述条件。那么我们可以很容易得到违反条件为：

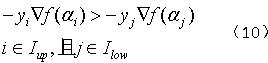
则根据式(8)中关于i的选择就可以明白select_working_set函数中关于选择i的部分了。

选择j

当yiyjK(i,j)为半正定矩阵时，当且仅当待优化乘子为“违反对”时，目标函数是严格递减的。LibSVM在做选择的时候，采用的是second order information方法。那么我们挑选出了i之后，剩下的任务就是挑选出既是“违反对”同时使目标函数值最小。补充一下：挑选了“违反对”，自然就使得目标函数自然递减了，那么我们挑选目标函数最小，自然使得迭代速度加快。这是我们希望看到的结果。

使用泰勒展开式：

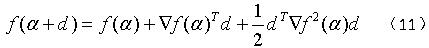
则优化问题变为：

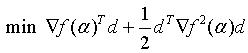
由约束条件可知：

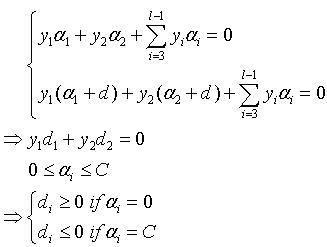
因为0≤α≤c,所以当α取到极值的时候，d的取值是有限制的，使得最终的α+d的值不会超出α取值范围。

则原优化问题可转换为下述优化问题：

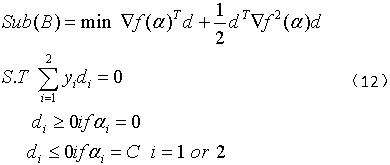
最小值为：

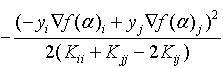
证明如下(可参考文献[3]的Theorem 3)：

结论貌似挺复杂的，其实不然，仔细观察发现式(13)其实就是一个一元二次函数，对其求极值，得该函数的最小值。

下面我们来看一下代码：

int Solver::select_working_set(int &out_i, int &out_j)
{
    // return i,j such that
    // i: maximizes -y_i * grad(f)_i, i in I_up(\alpha)
    // j: minimizes the decrease of obj value
    //    (if quadratic coefficeint <= 0, replace it with tau)
    //    -y_j*grad(f)_j < -y_i*grad(f)_i, j in I_low(\alpha)

    double Gmax = -INF;    //-yi*G(alphai)
    double Gmax2 = -INF;    //yj*G(alphaj)
    int Gmax_idx = -1;
    int Gmin_idx = -1;
    double obj_diff_min = INF;

    //寻找working set B中的i
    for (int t = 0; t<active_size; t++)
        if (y[t] == +1)
        {
            if (!is_upper_bound(t)) //对应于yi=1,alphai<c
                if (-G[t] >= Gmax)
                {
                    Gmax = -G[t];   //寻找最大的-yi*G(alphai)，以使违反条件最严重
                    Gmax_idx = t;
                }
        }
        else
        {
            if (!is_lower_bound(t)) //对应于yi=1,alphai>0
                if (G[t] >= Gmax)
                {
                    Gmax = G[t];
                    Gmax_idx = t;
                }
        }

    int i = Gmax_idx;   //得到i
    const Qfloat *Q_i = NULL;
    if (i != -1) // NULL Q_i not accessed: Gmax=-INF if i=-1
        Q_i = Q->get_Q(i, active_size);

    //寻找working set B中的j
    for (int j = 0; j<active_size; j++)
    {
        if (y[j] == +1)
        {
            if (!is_lower_bound(j))
            {
                double grad_diff = Gmax + G[j];    //分子(-yi*Gi+yj*Gj)
                if (G[j] >= Gmax2)  //寻找最小的-yj*G(alphaj)
                    Gmax2 = G[j];
                if (grad_diff > 0)      //保证不满足KKT条件
                {
                    double obj_diff;
                    double quad_coef = QD[i] + QD[j] - 2.0*y[i] * Q_i[j];    //分母(Kii+Kjj-2*Kij),注意Kij和Qij的关系(SVR_Q类中会讲)
                    if (quad_coef > 0)
                        obj_diff = -(grad_diff*grad_diff) / quad_coef;
                    else
                        obj_diff = -(grad_diff*grad_diff) / TAU;    //当quad_coef小于0时令其等于一个很小很小的值。

                    if (obj_diff <= obj_diff_min)
                    {
                        Gmin_idx = j;
                        obj_diff_min = obj_diff;
                    }
                }
            }
        }
        else
        {
            if (!is_upper_bound(j))
            {
                double grad_diff = Gmax - G[j];
                if (-G[j] >= Gmax2)
                    Gmax2 = -G[j];
                if (grad_diff > 0)
                {
                    double obj_diff;
                    double quad_coef = QD[i] + QD[j] + 2.0*y[i] * Q_i[j];
                    if (quad_coef > 0)
                        obj_diff = -(grad_diff*grad_diff) / quad_coef;
                    else
                        obj_diff = -(grad_diff*grad_diff) / TAU;

                    if (obj_diff <= obj_diff_min)
                    {
                        Gmin_idx = j;
                        obj_diff_min = obj_diff;
                    }
                }
            }
        }
    }

    if (Gmax + Gmax2 < eps || Gmin_idx == -1)    //达到停止条件或再没有需要优化的alpha，表示已经完全优化
        return 1;

    out_i = Gmax_idx;
    out_j = Gmin_idx;
    return 0;
}

void Solve(int l, const QMatrix& Q, const double *p_, const schar *y_, double *alpha_, double Cp, double Cn, double eps, SolutionInfo* si, int shrinking);

Solve函数用于求解更新alpha，下面讲解一下其求解原理，主要是SMO算法原理。这里主要还是以C-SVC为例，在后面讲解SVR_Q类时会解释如何将其扩展至回归分析。

SVM寻找超平面的公式为：

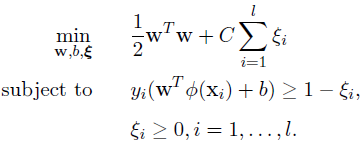
其对偶问题为：

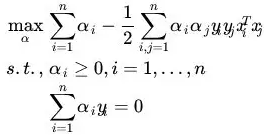
将其表示为矩阵形式可变换为：

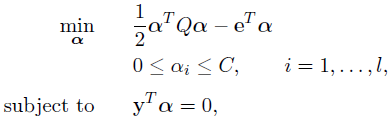
其中C>0为上界，e是数值全为1的行向量，Q是l*l的半正定矩阵，Qij=yi*yj*K(i,j)，K(i,j)=φ(Xi)^T*φ(Xj)为核函数。

当然，这只是LIBSVM中的C-SVC的目标公式，LIBSVM采用的是更加通用的目标公式：

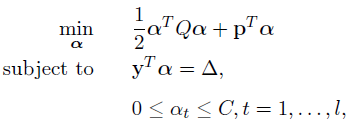
其中p是长度为l的行向量，△为常数。

其求导为：

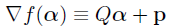
于是令aij = Kii+Kjj-2*Kij，假设选定的working set B为i和j，将其带入上式。（见文献[2]的Algorithm 1）
当aij>0时得：

当aij≤0时，约束同上式，令：

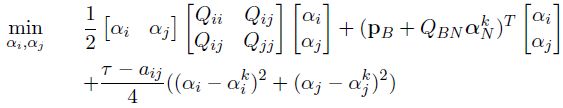
上式加的一项看似复杂，其实就是函数select_working_set中写的，当aij小于0时令其等于一个很小很小的值。

工作集i,j的选择
参见select_working_set函数的讲解。

αi,αj的更新
参考文献[2]的“5 Unbalanced Data”。

令：

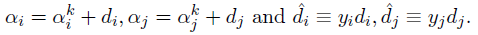
则问题：

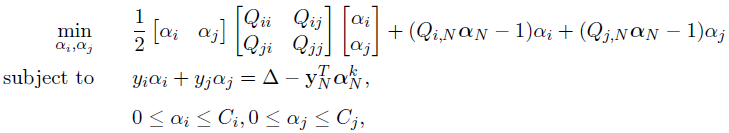
可转化为问题：

进而求解出di,dj可以得到更新后的α，即：

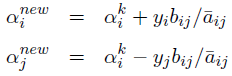
其中：

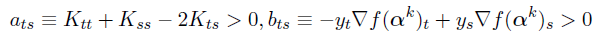
以不考虑非均衡样本为例(即Cp=Cn)。
当yi≠yj时：

当yi=yj时：

梯度G的更新
G[α(k)] = Q[α(k)] + p
G[α(k+1)] = Q[α(k+1)] + p
则：
G[α(k+1)] = G[α(k)] + Q[α(k+1)-α(k)]

G_bar的更新
G_bar[i] = {C * sum(Q[i,j]) while α[j]=C} i = 1,2,3,… l
因此，若α更新前后状态(alpha_status)不变，如都为C或都小于C，则G_bar不变。
否则：
①迭代前不为C，迭代后为C，则：
G_bar(k+1)[i] = {C * sum(Q[i,j]) while α[j]=C}
②迭代前为C，迭代后不为C，则：
G_bar(k+1)[i] = G_bar(k)[i] - {C * sum(Q[i,j]) while α[j]=C}

下面我们开始看代码。

void Solver::Solve(int l, const QMatrix& Q, const double *p_, const schar *y_,
    double *alpha_, double Cp, double Cn, double eps,
    SolutionInfo* si, int shrinking)
{
    this->l = l;
    this->Q = &Q;
    QD = Q.get_QD();
    clone(p, p_, l);
    clone(y, y_, l);
    clone(alpha, alpha_, l);
    this->Cp = Cp;
    this->Cn = Cn;
    this->eps = eps;
    unshrink = false;

    // initialize alpha_status
    {
        alpha_status = new char[l];
        for (int i = 0; i<l; i++)
            update_alpha_status(i);
    }

    // initialize active set (for shrinking)
    {
        active_set = new int[l];
        for (int i = 0; i<l; i++)
            active_set[i] = i;
        active_size = l;
    }

    // initialize gradient，根据梯度定义公式进行初始化
    {
        G = new double[l];
        G_bar = new double[l];
        int i;
        for (i = 0; i<l; i++)
        {
            G[i] = p[i];
            G_bar[i] = 0;
        }
        for (i = 0; i<l; i++)
            if (!is_lower_bound(i))
            {
                const Qfloat *Q_i = Q.get_Q(i, l);
                double alpha_i = alpha[i];
                int j;
                for (j = 0; j<l; j++)
                    G[j] += alpha_i * Q_i[j];
                if (is_upper_bound(i))
                    for (j = 0; j<l; j++)
                        G_bar[j] += get_C(i) * Q_i[j];
            }
    }

    // optimization step

    int iter = 0;
    int max_iter = max(10000000, l>INT_MAX / 100 ? INT_MAX : 100 * l);
    int counter = min(l, 1000) + 1;

    while (iter < max_iter)
    {
        // show progress and do shrinking

        if (--counter == 0)
        {
            counter = min(l, 1000);
            if (shrinking) do_shrinking();
            info("do shrinking.\n");
        }

        int i, j;
        if (select_working_set(i, j) != 0)
        {
            // reconstruct the whole gradient
            reconstruct_gradient();
            // reset active set size and check
            active_size = l;
            info("reconstruct G*\n");
            if (select_working_set(i, j) != 0) {
                info("======break======");
                break;
            }
            else
                counter = 1;    // do shrinking next iteration
        }
        ++iter;

        // update alpha[i] and alpha[j], handle bounds carefully

        const Qfloat *Q_i = Q.get_Q(i, active_size);
        const Qfloat *Q_j = Q.get_Q(j, active_size);

        double C_i = get_C(i);
        double C_j = get_C(j);

        double old_alpha_i = alpha[i];
        double old_alpha_j = alpha[j];

        if (y[i] != y[j])   //# yi,yj异号
        {
            double quad_coef = QD[i] + QD[j] + 2 * Q_i[j];  //最后一个为+号因为Qij为kij*y[i]*y[j]
            if (quad_coef <= 0)
                quad_coef = TAU;
            double delta = (-G[i] - G[j]) / quad_coef;  //alpha改变量
            double diff = alpha[i] - alpha[j];  //根据此项判断alpha(i)-alpha(j)=constant与约束框(0~c)的交点
            alpha[i] += delta;
            alpha[j] += delta;

            if (diff > 0)
            {
                if (alpha[j] < 0)
                {
                    alpha[j] = 0;
                    alpha[i] = diff;
                }
            }
            else
            {
                if (alpha[i] < 0)
                {
                    alpha[i] = 0;
                    alpha[j] = -diff;
                }
            }
            if (diff > C_i - C_j)
            {
                if (alpha[i] > C_i)
                {
                    alpha[i] = C_i;
                    alpha[j] = C_i - diff;
                }
            }
            else
            {
                if (alpha[j] > C_j)
                {
                    alpha[j] = C_j;
                    alpha[i] = C_j + diff;
                }
            }
        }
        else
        {
            double quad_coef = QD[i] + QD[j] - 2 * Q_i[j];
            if (quad_coef <= 0)
                quad_coef = TAU;
            double delta = (G[i] - G[j]) / quad_coef;
            double sum = alpha[i] + alpha[j];
            alpha[i] -= delta;
            alpha[j] += delta;

            if (sum > C_i)
            {
                if (alpha[i] > C_i)
                {
                    alpha[i] = C_i;
                    alpha[j] = sum - C_i;
                }
            }
            else
            {
                if (alpha[j] < 0)
                {
                    alpha[j] = 0;
                    alpha[i] = sum;
                }
            }
            if (sum > C_j)
            {
                if (alpha[j] > C_j)
                {
                    alpha[j] = C_j;
                    alpha[i] = sum - C_j;
                }
            }
            else
            {
                if (alpha[i] < 0)
                {
                    alpha[i] = 0;
                    alpha[j] = sum;
                }
            }
        }

        // update G

        double delta_alpha_i = alpha[i] - old_alpha_i;
        double delta_alpha_j = alpha[j] - old_alpha_j;
        for (int k = 0; k<active_size; k++)
        {
            G[k] += Q_i[k] * delta_alpha_i + Q_j[k] * delta_alpha_j;
        }

        // update alpha_status and G_bar

        {
            bool ui = is_upper_bound(i);
            bool uj = is_upper_bound(j);
            update_alpha_status(i);
            update_alpha_status(j);
            int k;
            if (ui != is_upper_bound(i))
            {
                Q_i = Q.get_Q(i, l);
                if (ui)
                    for (k = 0; k<l; k++)
                        G_bar[k] -= C_i * Q_i[k];
                else
                    for (k = 0; k<l; k++)
                        G_bar[k] += C_i * Q_i[k];
            }

            if (uj != is_upper_bound(j))
            {
                Q_j = Q.get_Q(j, l);
                if (uj)
                    for (k = 0; k<l; k++)
                        G_bar[k] -= C_j * Q_j[k];
                else
                    for (k = 0; k<l; k++)
                        G_bar[k] += C_j * Q_j[k];
            }
        }
        printf("i:%d, j:%d, alpha_i:%f, alpha_j:%f\n", i, j, alpha[i], alpha[j]);
    }

    if (iter >= max_iter)
    {
        if (active_size < l)
        {
            // reconstruct the whole gradient to calculate objective value
            reconstruct_gradient();
            active_size = l;
            info("*");
        }
        fprintf(stderr, "\nWARNING: reaching max number of iterations\n");
    }

    // calculate rho

    si->rho = calculate_rho();

    // calculate objective value
    {
        double v = 0;
        int i;
        for (i = 0; i<l; i++)
            v += alpha[i] * (G[i] + p[i]);

        si->obj = v / 2;    //目标值为(alpha^T*Q*alpha + p^T*alpha)
    }

    // put back the solution
    {
        for (int i = 0; i<l; i++)
            alpha_[active_set[i]] = alpha[i];
    }

    // juggle everything back
    /*{
    for(int i=0;i<l;i++)
    while(active_set[i] != i)
    swap_index(i,active_set[i]);
    // or Q.swap_index(i,active_set[i]);
    }*/

    si->upper_bound_p = Cp;
    si->upper_bound_n = Cn;

    info("\noptimization finished, #iter = %d\n", iter);
    /*for (int g = 0; g < l/2; g++) {
        printf("alpha_%d:%f\n", g, (alpha[g]-alpha[g+l/2]));
    }*/

    delete[] p;
    delete[] y;
    delete[] alpha;
    delete[] alpha_status;
    delete[] active_set;
    delete[] G;
    delete[] G_bar;
}

virtual double calculate_rho();

该函数用于计算判别函数中的b(rho为b的相反数)，参考文献[2]的3.6。
这里仅写出结果：
当yi=1时：
假设0<αi<C，则r1 = G[α](i)
为避免出现数值错误，一般将其写成平均值：

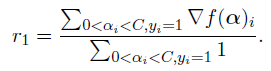
如果没有这样的αi，则r1必须满足：

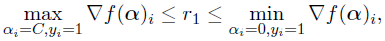
此时将ri取为范围中点。
当yi=-1时，计算过程类似，得到r2。

得到r1、r2后，通过计算得到：

double Solver::calculate_rho()
{
    double r;
    int nr_free = 0;
    double ub = INF, lb = -INF, sum_free = 0;
    for (int i = 0; i<active_size; i++)
    {
        double yG = y[i] * G[i];

        if (is_upper_bound(i))
        {
            if (y[i] == -1)
                ub = min(ub, yG);
            else
                lb = max(lb, yG);
        }
        else if (is_lower_bound(i))
        {
            if (y[i] == +1)
                ub = min(ub, yG);
            else
                lb = max(lb, yG);
        }
        else
        {
            ++nr_free;
            sum_free += yG;
        }
    }

    if (nr_free>0)
        r = sum_free / nr_free;
    else
        r = (ub + lb) / 2;

    return r;
}

SVR_Q类

class SVR_Q : public Kernel
{
public:
    SVR_Q(const svm_problem& prob, const svm_parameter& param)
        :Kernel(prob.l, prob.x, param)
    {
        l = prob.l;
        cache = new Cache(l, (long int)(param.cache_size*(1 << 20)));
        QD = new double[2 * l];
        sign = new schar[2 * l];
        index = new int[2 * l];
        for (int k = 0; k<l; k++)
        {
            sign[k] = 1;
            sign[k + l] = -1;
            index[k] = k;
            index[k + l] = k;
            QD[k] = (this->*kernel_function)(k, k);
            QD[k + l] = QD[k];
        }
        buffer[0] = new Qfloat[2 * l];
        buffer[1] = new Qfloat[2 * l];
        next_buffer = 0;
    }

    void swap_index(int i, int j) const
    {
        swap(sign[i], sign[j]);
        swap(index[i], index[j]);
        swap(QD[i], QD[j]);
    }

    Qfloat *get_Q(int i, int len) const
    {
        Qfloat *data;
        int j, real_i = index[i];
        if (cache->get_data(real_i, &data, l) < l)
        {
            for (j = 0; j<l; j++)
                data[j] = (Qfloat)(this->*kernel_function)(real_i, j);
        }

        // reorder and copy
        Qfloat *buf = buffer[next_buffer];
        next_buffer = 1 - next_buffer;
        schar si = sign[i];
        for (j = 0; j<len; j++)
            buf[j] = (Qfloat)si * (Qfloat)sign[j] * data[index[j]];
        return buf;
    }

    double *get_QD() const
    {
        return QD;
    }

    ~SVR_Q()
    {
        delete cache;
        delete[] sign;
        delete[] index;
        delete[] buffer[0];
        delete[] buffer[1];
        delete[] QD;
    }
private:
    int l;
    Cache *cache;
    schar *sign;
    int *index;
    mutable int next_buffer;
    Qfloat *buffer[2];
    double *QD;
};

成员变量

主要参数解释如下：

Parameter	Interpretation
*sign	同SVC_Q中的y，即为公式中的y。sign[i]=1,sign[i+l]=-1,i=1,2,3,…,l

成员函数

SVR_Q(const svm_problem& prob, const svm_parameter& param):Kernel(prob.l, prob.x, param);

初始化有关SVR的计算参数。与SVC不同的是优化公式中的y并不是SVR样本数据的目标值，优化公式中的l为两倍的SVR数据样本数量，详见solve_epsilon_svr函数解析。

SVR_Q(const svm_problem& prob, const svm_parameter& param)
        :Kernel(prob.l, prob.x, param)
    {
        l = prob.l;    //l为样本数据的数量
        cache = new Cache(l, (long int)(param.cache_size*(1 << 20)));
        //对于SVR而言需要开辟2*l的空间
        QD = new double[2 * l];
        sign = new schar[2 * l];
        index = new int[2 * l];

        for (int k = 0; k<l; k++)
        {
            //sign[i]=1,sign[i+l]=-1,i=1,2,3,...,l
            sign[k] = 1;
            sign[k + l] = -1;

            index[k] = k;
            index[k + l] = k;

            QD[k] = (this->*kernel_function)(k, k);
            QD[k + l] = QD[k];
        }
        buffer[0] = new Qfloat[2 * l];
        buffer[1] = new Qfloat[2 * l];
        next_buffer = 0;
    }

Qfloat *get_Q(int i, int len) const;

计算SVR公式中所使用的Q[i]，此处为第i列，不过一般而言Q[i,j]=Q[j,i]。

    Qfloat *get_Q(int i, int len) const
    {
        Qfloat *data;
        int j, real_i = index[i];
        if (cache->get_data(real_i, &data, l) < l)
        {
            for (j = 0; j<l; j++)
                data[j] = (Qfloat)(this->*kernel_function)(real_i, j);    //计算得到K[i,j]
        }   

        // reorder and copy
        Qfloat *buf = buffer[next_buffer];
        next_buffer = 1 - next_buffer;
        schar si = sign[i];
        for (j = 0; j<len; j++)
            buf[j] = (Qfloat)si * (Qfloat)sign[j] * data[index[j]];    //为了与Solver类中的公式相匹配，此处定义Q[i,j]=sign[i]*sign[j]*K[i,j]
        return buf;
    }

static void solve_epsilon_svr(const svm_problem *prob, const svm_parameter *param, double *alpha, Solver::SolutionInfo* si)

该函数用于计算优化公式中的p，并定义Solver中的y与α，调用Solver类。

epsilon-SVR原始公式为：

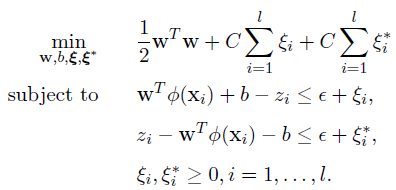
其对偶式为：

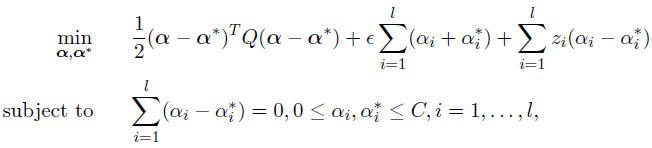
其中：

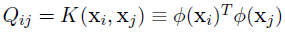
决策函数为：

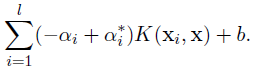
将其化为矩阵形式：

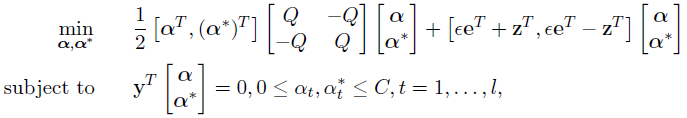
其中y为2l*1的矩阵，yt=1，t=1,…,l; yt=-1，t=l+1,…,2l.

将上式与前述的通用目标公式相比较，记上标t为通用公式的参数，则可知：

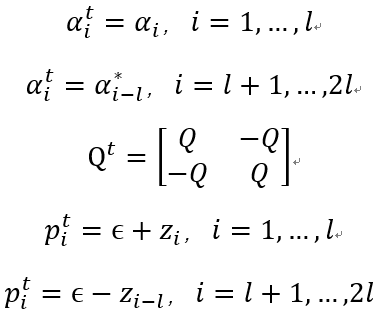
static void solve_epsilon_svr(
    const svm_problem *prob, const svm_parameter *param,
    double *alpha, Solver::SolutionInfo* si)
{
    int l = prob->l;
    double *alpha2 = new double[2 * l];
    double *linear_term = new double[2 * l];
    schar *y = new schar[2 * l];    //新定义了y值，对应Solver的y
    int i;

    for (i = 0; i<l; i++)
    {
        alpha2[i] = 0;
        linear_term[i] = param->p - prob->y[i];    //epsilon*e-z,epsilon为间隔带，e为全为1的行向量，z为样本数据的目标值
        y[i] = 1;

        alpha2[i + l] = 0;
        linear_term[i + l] = param->p + prob->y[i];    //epsilon*e+z
        y[i + l] = -1;
    }

    Solver s;
    s.Solve(2 * l, SVR_Q(*prob, *param), linear_term, y,
        alpha2, param->C, param->C, param->eps, si, param->shrinking);

    double sum_alpha = 0;
    for (i = 0; i<l; i++)
    {
        alpha[i] = alpha2[i] - alpha2[i + l];    //将alpha[i]-alpha[i+1]得到数据样本x前的最终系数
        sum_alpha += fabs(alpha[i]);
    }
    info("nu = %f\n", sum_alpha / (param->C*l));

    delete[] alpha2;
    delete[] linear_term;
    delete[] y;
}

static decision_function svm_train_one(const svm_problem *prob, const svm_parameter *param, double Cp, double Cn)

根据kernel_type的不同调用不同的求解函数，并计算支持向量的个数与处于边界的支持向量个数。

static decision_function svm_train_one(
    const svm_problem *prob, const svm_parameter *param,
    double Cp, double Cn)
{
    double *alpha = Malloc(double, prob->l);
    Solver::SolutionInfo si;
    switch (param->svm_type)
    {
    case C_SVC:
        solve_c_svc(prob, param, alpha, &si, Cp, Cn);
        break;
    case NU_SVC:
        solve_nu_svc(prob, param, alpha, &si);
        break;
    case ONE_CLASS:
        solve_one_class(prob, param, alpha, &si);
        break;
    case EPSILON_SVR:
        solve_epsilon_svr(prob, param, alpha, &si);
        break;
    case NU_SVR:
        solve_nu_svr(prob, param, alpha, &si);
        break;
    }

    info("obj = %f, rho = %f\n", si.obj, si.rho);

    // output SVs

    int nSV = 0;
    int nBSV = 0;
    for (int i = 0; i<prob->l; i++)
    {
        if (fabs(alpha[i]) > 0)
        {
            ++nSV;
            if (prob->y[i] > 0)
            {
                if (fabs(alpha[i]) >= si.upper_bound_p)
                    ++nBSV;
            }
            else
            {
                if (fabs(alpha[i]) >= si.upper_bound_n)
                    ++nBSV;
            }
        }
    }

    info("nSV = %d, nBSV = %d\n", nSV, nBSV);

    decision_function f;
    f.alpha = alpha;
    f.rho = si.rho;
    return f;
}

svm_model *svm_train(const svm_problem *prob, const svm_parameter *param)；

根据不同svm_type开辟不同空间，最后返回训练好的svm model。

svm_model *svm_train(const svm_problem *prob, const svm_parameter *param)
{
    svm_model *model = Malloc(svm_model, 1);
    model->param = *param;
    model->free_sv = 0; // XXX

    if (param->svm_type == ONE_CLASS ||
        param->svm_type == EPSILON_SVR ||
        param->svm_type == NU_SVR)
    {
        // regression or one-class-svm
        model->nr_class = 2;
        model->label = NULL;
        model->nSV = NULL;
        model->probA = NULL; model->probB = NULL;
        model->sv_coef = Malloc(double *, 1);

        /*if (param->probability &&
            (param->svm_type == EPSILON_SVR ||
                param->svm_type == NU_SVR))
        {
            model->probA = Malloc(double, 1);
            model->probA[0] = svm_svr_probability(prob, param);
        }*/

        decision_function f = svm_train_one(prob, param, 0, 0);
        model->rho = Malloc(double, 1);
        model->rho[0] = f.rho;

        int nSV = 0;
        int i;
        for (i = 0; i<prob->l; i++)
            if (fabs(f.alpha[i]) > 0) ++nSV;
        model->l = nSV;
        model->SV = Malloc(svm_node *, nSV);
        model->sv_coef[0] = Malloc(double, nSV);
        model->sv_indices = Malloc(int, nSV);
        int j = 0;
        for (i = 0; i<prob->l; i++)
            if (fabs(f.alpha[i]) > 0)
            {
                model->SV[j] = prob->x[i];
                model->sv_coef[0][j] = f.alpha[i];
                model->sv_indices[j] = i + 1;
                ++j;
            }

        free(f.alpha);
    }
    else
    {
        // classification
        int l = prob->l;
        int nr_class;
        int *label = NULL;
        int *start = NULL;
        int *count = NULL;
        int *perm = Malloc(int, l);

        // group training data of the same class
        svm_group_classes(prob, &nr_class, &label, &start, &count, perm);
        if (nr_class == 1)
            info("WARNING: training data in only one class. See README for details.\n");

        svm_node **x = Malloc(svm_node *, l);
        int i;
        for (i = 0; i<l; i++)
            x[i] = prob->x[perm[i]];

        // calculate weighted C

        double *weighted_C = Malloc(double, nr_class);
        for (i = 0; i<nr_class; i++)
            weighted_C[i] = param->C;
        for (i = 0; i<param->nr_weight; i++)
        {
            int j;
            for (j = 0; j<nr_class; j++)
                if (param->weight_label[i] == label[j])
                    break;
            if (j == nr_class)
                fprintf(stderr, "WARNING: class label %d specified in weight is not found\n", param->weight_label[i]);
            else
                weighted_C[j] *= param->weight[i];
        }

        // train k*(k-1)/2 models

        bool *nonzero = Malloc(bool, l);
        for (i = 0; i<l; i++)
            nonzero[i] = false;
        decision_function *f = Malloc(decision_function, nr_class*(nr_class - 1) / 2);

        double *probA = NULL, *probB = NULL;
        if (param->probability)
        {
            probA = Malloc(double, nr_class*(nr_class - 1) / 2);
            probB = Malloc(double, nr_class*(nr_class - 1) / 2);
        }

        int p = 0;
        for (i = 0; i<nr_class; i++)
            for (int j = i + 1; j<nr_class; j++)
            {
                svm_problem sub_prob;
                int si = start[i], sj = start[j];
                int ci = count[i], cj = count[j];
                sub_prob.l = ci + cj;
                sub_prob.x = Malloc(svm_node *, sub_prob.l);
                sub_prob.y = Malloc(double, sub_prob.l);
                int k;
                for (k = 0; k<ci; k++)
                {
                    sub_prob.x[k] = x[si + k];
                    sub_prob.y[k] = +1;
                }
                for (k = 0; k<cj; k++)
                {
                    sub_prob.x[ci + k] = x[sj + k];
                    sub_prob.y[ci + k] = -1;
                }

                if (param->probability)
                    svm_binary_svc_probability(&sub_prob, param, weighted_C[i], weighted_C[j], probA[p], probB[p]);

                f[p] = svm_train_one(&sub_prob, param, weighted_C[i], weighted_C[j]);
                for (k = 0; k<ci; k++)
                    if (!nonzero[si + k] && fabs(f[p].alpha[k]) > 0)
                        nonzero[si + k] = true;
                for (k = 0; k<cj; k++)
                    if (!nonzero[sj + k] && fabs(f[p].alpha[ci + k]) > 0)
                        nonzero[sj + k] = true;
                free(sub_prob.x);
                free(sub_prob.y);
                ++p;
            }

        // build output

        model->nr_class = nr_class;

        model->label = Malloc(int, nr_class);
        for (i = 0; i<nr_class; i++)
            model->label[i] = label[i];

        model->rho = Malloc(double, nr_class*(nr_class - 1) / 2);
        for (i = 0; i<nr_class*(nr_class - 1) / 2; i++)
            model->rho[i] = f[i].rho;

        if (param->probability)
        {
            model->probA = Malloc(double, nr_class*(nr_class - 1) / 2);
            model->probB = Malloc(double, nr_class*(nr_class - 1) / 2);
            for (i = 0; i<nr_class*(nr_class - 1) / 2; i++)
            {
                model->probA[i] = probA[i];
                model->probB[i] = probB[i];
            }
        }
        else
        {
            model->probA = NULL;
            model->probB = NULL;
        }

        int total_sv = 0;
        int *nz_count = Malloc(int, nr_class);
        model->nSV = Malloc(int, nr_class);
        for (i = 0; i<nr_class; i++)
        {
            int nSV = 0;
            for (int j = 0; j<count[i]; j++)
                if (nonzero[start[i] + j])
                {
                    ++nSV;
                    ++total_sv;
                }
            model->nSV[i] = nSV;
            nz_count[i] = nSV;
        }

        info("Total nSV = %d\n", total_sv);

        model->l = total_sv;
        model->SV = Malloc(svm_node *, total_sv);
        model->sv_indices = Malloc(int, total_sv);
        p = 0;
        for (i = 0; i<l; i++)
            if (nonzero[i])
            {
                model->SV[p] = x[i];
                model->sv_indices[p++] = perm[i] + 1;
            }

        int *nz_start = Malloc(int, nr_class);
        nz_start[0] = 0;
        for (i = 1; i<nr_class; i++)
            nz_start[i] = nz_start[i - 1] + nz_count[i - 1];

        model->sv_coef = Malloc(double *, nr_class - 1);
        for (i = 0; i<nr_class - 1; i++)
            model->sv_coef[i] = Malloc(double, total_sv);

        p = 0;
        for (i = 0; i<nr_class; i++)
            for (int j = i + 1; j<nr_class; j++)
            {
                // classifier (i,j): coefficients with
                // i are in sv_coef[j-1][nz_start[i]...],
                // j are in sv_coef[i][nz_start[j]...]

                int si = start[i];
                int sj = start[j];
                int ci = count[i];
                int cj = count[j];

                int q = nz_start[i];
                int k;
                for (k = 0; k<ci; k++)
                    if (nonzero[si + k])
                        model->sv_coef[j - 1][q++] = f[p].alpha[k];
                q = nz_start[j];
                for (k = 0; k<cj; k++)
                    if (nonzero[sj + k])
                        model->sv_coef[i][q++] = f[p].alpha[ci + k];
                ++p;
            }

        free(label);
        free(probA);
        free(probB);
        free(count);
        free(perm);
        free(start);
        free(x);
        free(weighted_C);
        free(nonzero);
        for (i = 0; i<nr_class*(nr_class - 1) / 2; i++)
            free(f[i].alpha);
        free(f);
        free(nz_count);
        free(nz_start);
    }
    return model;
}

double svm_predict_values(const svm_model *model, const svm_node *x, double* dec_values)

该函数用于预测单个测试样本数据，因此对于一组测试样本需要调用n次。

double svm_predict_values(const svm_model *model, const svm_node *x, double* dec_values)
{
    int i;
    if (model->param.svm_type == ONE_CLASS ||
        model->param.svm_type == EPSILON_SVR ||
        model->param.svm_type == NU_SVR)
    {
        double *sv_coef = model->sv_coef[0];
        double sum = 0;
        for (i = 0; i<model->l; i++)
            sum += sv_coef[i] * Kernel::k_function(x, model->SV[i], model->param);    //对应决策公式的前半部分，即αi*K(xi,x)
        sum -= model->rho[0];    //加上决策函数的常数项
        *dec_values = sum;

        if (model->param.svm_type == ONE_CLASS)
            return (sum>0) ? 1 : -1;
        else
            return sum;
    }
    else
    {
        int nr_class = model->nr_class;
        int l = model->l;

        double *kvalue = Malloc(double, l);
        for (i = 0; i<l; i++)
            kvalue[i] = Kernel::k_function(x, model->SV[i], model->param);

        int *start = Malloc(int, nr_class);
        start[0] = 0;
        for (i = 1; i<nr_class; i++)
            start[i] = start[i - 1] + model->nSV[i - 1];

        int *vote = Malloc(int, nr_class);
        for (i = 0; i<nr_class; i++)
            vote[i] = 0;

        int p = 0;
        for (i = 0; i<nr_class; i++)
            for (int j = i + 1; j<nr_class; j++)
            {
                double sum = 0;
                int si = start[i];
                int sj = start[j];
                int ci = model->nSV[i];
                int cj = model->nSV[j];

                int k;
                double *coef1 = model->sv_coef[j - 1];
                double *coef2 = model->sv_coef[i];
                for (k = 0; k<ci; k++)
                    sum += coef1[si + k] * kvalue[si + k];
                for (k = 0; k<cj; k++)
                    sum += coef2[sj + k] * kvalue[sj + k];
                sum -= model->rho[p];
                dec_values[p] = sum;

                if (dec_values[p] > 0)
                    ++vote[i];
                else
                    ++vote[j];
                p++;
            }

        int vote_max_idx = 0;
        for (i = 1; i<nr_class; i++)
            if (vote[i] > vote[vote_max_idx])
                vote_max_idx = i;

        free(kvalue);
        free(start);
        free(vote);
        return model->label[vote_max_idx];
    }
}

---

Reference:

[1] Smola A J, Schölkopf B. A tutorial on support vector regression[J]. Statistics & Computing, 2004, volume 14(3):199-222(24).
[2] Chang C C, Lin C J. LIBSVM: A library for support vector machines[M]. ACM, 2011.
[3] Fan R E, Chen P H, Lin C J, et al. Working Set Selection Using Second Order Information for Training Support Vector Machines[J]. Journal of Machine Learning Research, 2005, 6(4):1889-1918.
[4] Svm O F. Sequential Minimal Optimization for SVM[J]. 2007.
[5] LibSVM中select_working_set函数：http://blog.csdn.net/le_zhou/article/details/40505465
[6] libsvm最新源代码（版本3.21）理解解析（三）：http://blog.csdn.net/xiaoqiangqiangjie/article/details/53886907
[7] LibSVM源码剖析（java版）：http://makaidong.com/bentuwuying/21760_40631.html
[8] LibSVM-2.6 程序代码注释,上交

---

本博客与https://xuyunkun.com同步更新