python3 || 高斯混合模型GMM

GMM模型的python实现

预备知识：

EM算法原理

GMM算法原理

友情提示：本代码配合GMM算法原理中的步骤阅读更佳哦！

本文分为一元高斯分布的EM算法以及多元高斯分布的EM算法，分别采用两本书上的数据《统计学习方法》和《机器学习》。

一元高斯混合模型

python未完成，可以看R实现的。 R || 高斯混合模型GMM

多元高斯混合模型

多元高斯混合模型采用的是《机器学习》中的西瓜数据集。

多元高斯分布中的密度值python中没有直接函数，需要自己编写

import numpy as np
# 高斯分布的概率密度函数
def dnorm(x,u,sigma2):
    """
    x:样本
    u:均值
    sigma2:方差或协差阵
    """
    if not isinstance(sigma2,np.matrix):
        sigma2 = np.mat(sigma2)
    if not isinstance(x,np.matrix):
        x=np.mat(x)   
    n = np.shape(x)[1]
    expOn = float(-0.5 * (x-u) * sigma2.I * (x-u).T)  
    #python中一维矩阵默认为行向量，所以和书上公式有差异
    divBy = np.sqrt(pow(2*np.pi,n)) * pow(np.linalg.det(sigma2),0.5)
    return pow(np.e,expOn) / divBy

接下来可以直接编写聚类的函数。

def GaussCluster(data,k,a,u,sigma2):
    """
    #data:数据集,向量或数据框
    #k:聚类的个数，或高斯分布的个数
    #a0:高斯分布的先验概率,选择各个高斯分布的概率,向量
    #u0:高斯分布的初始均值
    #sigma2:一元高斯分布即为方差，多元即为协方差,sigma为标准差,
    """
    if not isinstance(data,np.matrix):
        data = np.mat(data)

    N = np.shape(data)[0]
    col = np.shape(data)[1]
    covList = [sigma2 for x in range(k)]
    count = 0
    while True:
        #u0 = u
        p = np.zeros([N,k])
        for i in range(N):
            for j in range(k):
                p[i,j] = dnorm(data[i,],u[j,],covList[j])
        aarray = np.tile(a,(N,1))        
        r = (p * aarray)  / np.tile(np.sum(p * aarray,axis = 1),(3,1)).T  #p * aarray 两个array相乘，为对应元素相乘
        u = np.array(r.T * data) / np.tile(np.sum(r,axis = 0),(2,1)).T     
        for j in range(k):
            sigma = np.zeros([col,col])
            for i in range(N):
                sigma += r[i,j] * (data[i,] - u[j,]).T * (data[i,] - u[j,])
            covList[j] = sigma/sum(r[:,j])
        a = np.sum(r,axis = 0) / N
        count += 1
        if count == 100:
            break
    cluster = np.vstack((np.array(range(N)),np.argmax(r,axis = 1))).T
    return u,covList,a,clusterv('watermelon.csv')
data = as.matrix(wamellondata[,2:3])
a = c(1/3,1/3,1/3)
u = rbind(data[6,],data[22,],data[27,])
cov0 <- matrix(c(0.1,0,0,0.1),ncol = 2)
list=mulGaussCluster(data,k=3,a,u,cov0)
cluster = list$cluster

• 需要区分numpy中 array * array | matrix * matrix | array * matrix
• 复制数据 np.tile()
• 找出数组中每行最大的值对应的列 np.argmax(）
• 注意python中向量(一维数组)默认为行向量，R中向量默认为列向量，理论书一般向量默认为列向量

下一步，设定初始值，进行函数调用

data = np.loadtxt(open("watermelon.csv","rb"),delimiter=",",skiprows = 0)
a=np.array([1/3,1/3,1/3])
u = np.vstack((data[5,],data[21,],data[26,]))
sigma2 = np.array([[0.1,0],[0,0.1]])

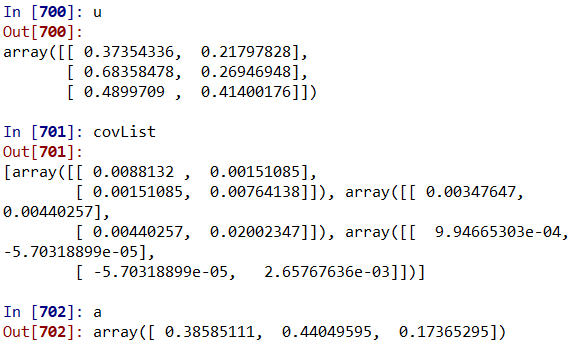
u,covList,a,cluster = GaussCluster(data,k,a,u,sigma2)

结果：

参考网址：
R || 高斯混合模型GMM

R实现一维高斯分布混合模型

python实现多维高斯分布模型