市场营销问题（三）：机票的销售策略

最新推荐文章于 2020-09-25 01:20:59 发布

wamg潇潇

最新推荐文章于 2020-09-25 01:20:59 发布

阅读量4k

点赞数 1

分类专栏： matlab数学建模

本文链接：https://blog.csdn.net/qq_29831163/article/details/89413496

版权

matlab数学建模专栏收录该内容

109 篇文章

订阅专栏

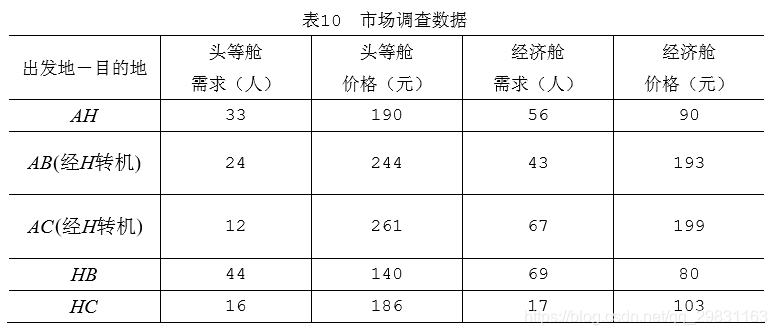
某航空公司每天有三个航班服务于 A ,B ,C, H四个城市，其中城市H 是可供转机使用的。三个航班的出发地－目的地分别为 AH ,HB, HC ，可搭乘旅客的大数量分别为120人，100人，110人，机票的价格分头等舱和经济舱两类。经过市场调查，公司销售部得到了每天旅客的相关信息，见表10。该公司应该在每条航线上分别分配多少头等舱和经济舱的机票？

（1）问题分析

公司的目标应该是使销售收入最大化，由于头等舱的机票价格大于对应的经济舱的机票价格，很容易让人想到先满足所有头等舱的顾客需求：这样 AH 上的头等舱数量 =33+24+12=69，HB上的头等舱数量=24+44=68，HC 上的头等舱数量=12+16=28，等等，但这种贪婪算法是否一定得到好的销售计划？

（2）模型建立

考虑5个起终点航线AH ,AB ,AC,HB ，HC依次编号为i（i=1,2,..,5），相应的头等舱需求记为 $\small a_{i}$ ，价格记为 $\small p_{i}$ ；相应的经济舱需求记为 $\small b_{i}$ ，价格记为 $\small q_{i}$ 。此外，三个航班AH ,HB, HC的顾客容量分别是 $\small c_{1}$ =120 ， $\small c_{2}$ =100 ， $\small c_{3}$ = 110 。这就是例中给出的全部数据。

设航线i（i =1,2,...,5 ）上销售的头等舱机票数为 $\small x_{i}$ ，销售的经济舱机票数为 $\small y_{i}$ ，这就是决策变量。显然，目标函数应该是

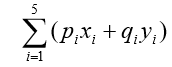（ 1 ）

约束条件有以下两类：

i）三个航班上的容量限制

例如，航班 AH 上的乘客应当是购买 AH ,AB ,AC 机票的所有旅客，所以

（ 2 ）

同理，有

（ 3 ）

ii）每条航线上的需求限制

（ 4 ）

（3）模型求解

MODEL: 
TITLE 机票销售计划; 
SETS:     
    route /AH,AB,AC,HB,HC/:a,b,p,q,x,y; 
ENDSETS 
DATA: 
a p b q= 
    33 190 56 90 
    24 244 43 193 
    12 261 67 199 
    44 140 69 80 
    16 186 17 103 ; 
c1 c2 c3 = 120 100 110; 
ENDDATA 
[obj] Max = @SUM(route: p*x+q*y ); 
[AH] @SUM(route(i)|i#ne#4#and#i#ne#5:x(i)+y(i)) < c1; 
[HB] @SUM(route(i)|i#eq#2#or#i#eq#4:x(i)+y(i))  < c2; 
[HC] @SUM(route(i)|i#eq#3#or#i#eq#5:x(i)+y(i))  < c3; 
@FOR(route: @bnd(0,x,a);@bnd(0,y,b) ); 
END

计算结果为，航线AH ,AB ,AC,HB,HC 上分别销售33，10，12，44，16张头等舱机票，分别销售0，0，65，46，17张经济舱机票，总销售收入为39344元。从三个约束的松弛/剩余（slack or surplus）均为0可知，机上已经全部满员。

（4）结果讨论

按道理，机票张数还应该有整数约束。这里直接按连续线性规划解，得到的解已经都是整数，所以也就没有必要再加上整数约束了。后我们指出：最优解中 AB 线路上头等舱的需求（24人）并没有全部得到满足，所以本节开始时介绍的贪婪算法的思想是不能保证求到最优解的。事实上，读者不难求出贪婪算法得到的解对应的总销售额是38854元，小于这里的优值39344元。