常微分方程的解法 (一): 常微分方程的离散化 :差商近似导数、数值积分方法、Taylor 多项式近似

---

常微分方程的解法求解系列博文：

常微分方程的解法 (一): 常微分方程的离散化 :差商近似导数、数值积分方法、Taylor 多项式近似

常微分方程的解法 (二): 欧拉（Euler）方法

常微分方程的解法 (三): 龙格—库塔（Runge—Kutta）方法 、线性多步法

常微分方程的解法 (四): Matlab 解法

---

目录

1 常微分方程的离散化  

数值解法

（i）用差商近似导数------差分方程初值问题

       （ii）用数值积分方法

      （iii）Taylor 多项式近似

---

建立微分方程只是解决问题的第一步，通常需要求出方程的解来说明实际现象，并 加以检验。如果能得到解析形式的解固然是便于分析和应用的，但是我们知道，只有线 性常系数微分方程，并且自由项是某些特殊类型的函数时，才可以肯定得到这样的解， 而绝大多数变系数方程、非线性方程都是所谓“解不出来”的，即使看起来非常简单的 方程如  ，于是对于用微分方程解决实际问题来说，数值解法就是一个十 分重要的手段.

1 常微分方程的离散化

下面主要讨论一阶常微分方程的初值问题，其一般形式是

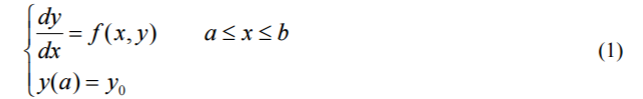
在下面的讨论中，我们总假定函数 f (x, y) 连续，且关于 y 满足李普希兹(Lipschitz)条 件，即存在常数 L ，使得

这样，由常微分方程理论知，初值问题(1)的解必定存在唯一。

数值解法

所谓数值解法，就是求问题（1）的解 y(x) 在若干点           

建立数值解法，首先要将微分方程离散化，一般采用以下几种方法：

（i）用差商近似导数------差分方程初值问题

需要说明的是，用不同的差商近似导数，将得到不同的计算公式。

（ii）用数值积分方法

将问题（1）的解表成积分形式，用数值积分方法离散化。例如，对微分方程两端 积分，得

右边的积分用矩形公式或梯形公式计算。

（iii）Taylor 多项式近似

以上三种方法都是将微分方程离散化的常用方法，每一类方法又可导出不同形式的 计算公式。其中的 Taylor 展开法，不仅可以得到求数值解的公式，而且容易估计截断 误差。

---

常微分方程的解法求解系列博文：

常微分方程的解法 (一): 常微分方程的离散化 :差商近似导数、数值积分方法、Taylor 多项式近似

常微分方程的解法 (二): 欧拉（Euler）方法

常微分方程的解法 (三): 龙格—库塔（Runge—Kutta）方法 、线性多步法

常微分方程的解法 (四): Matlab 解法

---