【Python】用蒙特卡洛树搜索（MCTS）解决寻路问题

百万光年

已于 2024-09-14 14:08:27 修改

阅读量9.2k

点赞数 20

分类专栏： Python 机器学习文章标签：机器学习蒙特卡洛树搜索 python

于 2021-03-07 01:02:17 首次发布

本文链接：https://blog.csdn.net/qq_30082991/article/details/114023556

版权

Python 同时被 2 个专栏收录

5 篇文章

订阅专栏

机器学习

1 篇文章

订阅专栏

本文探讨如何利用蒙特卡洛树搜索（MCTS）解决寻路问题，对比了DFS和BFS，介绍了MCTS在决策树上的优势。通过MCTS算法，实现了在障碍物地图上从起点到终点的路径搜索，讨论了算法的基本假设、权值计算和加权随机策略。实验展示了不同地图规模和参数设置下的运行结果，分析了算法效率和收敛速度。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

像人类一样思考。

文章目录

用蒙特卡洛树搜索（MCTS）解决寻路问题

用蒙特卡洛树搜索（MCTS）解决寻路问题

关于蒙特卡洛树搜索

深度优先搜索(Deep First Search, DFS)、广度优先搜索(Breadth First Search, BFS)是最常用、最简单，也最为人所熟知的两种搜索模式。DFS优先探向更深的节点，而BFS则不把当前深度的节点探完绝不向更深迈出一步。

它们的固有特点就是，哪怕（从人——或者说上帝——的角度来看）最优解近在咫尺，它们各自也会老老实实的搜完当前子树（或是当前层）再迈出下一步。这也是层出不穷的搜索剪枝方法试图避免的情况：一些无用的节点明明没有必要花费宝贵的时间去试探。

那么，有没有一种搜索策略可以同时拥有DFS和BFS的优势，又能取长补短避免它们的缺点呢？

蒙特卡洛树搜索(Monte Carlo Tree Search, MCTS)是一种搜索策略，严格来说它和DFS、BFS是相当的。不同之处在于，它通过一个权重表（取决于具体的实现）来决定每次搜索的试探方向：到底是探向更深的一层，还是停留在当前层试探其他节点。

因此，MCTS是一种兼而有之的搜索策略——它估计当前节点和最优解的距离，启发式地决定到底应该采用类DFS的搜索模式，还是采用类BFS的搜索方式。因此，它可以兼具两者的优势并弥补其不足。

最有名的MCTS应用应当就是AlphaGo了。上一个在决策树上胜过人类的前辈“深蓝”还是靠算力和搜索优化和人类硬碰硬，而AlphaGo则是搭乘着ML/AI的快车大步流星地将人类的智力远远地甩在了后面。基于MCTS的试探方式和大数据训练的损失函数，AlphaGo比所有前辈更像“人”——在决策问题上忠实地模拟着“贪心策略”这一人类解决决策问题时最常用的解法。
MCTS解决对弈型问题

寻路问题和寻路算法

游戏业界的AI开发者有一句名言：

寻路已不是问题。¹

提到寻路算法，朴素的BFS和Dijsktra固然能解决问题，不过工业上更常用的是A*算法²和NAV导航网格寻路，以及各种预定义路径点的静态寻路。可以说，这已经不是一个亟需解决的“问题”，而是“一题多解”和“算法改进”的舞台。然而，A*和NAV等等工业算法已经足够优秀，很难再上演像“AlphaGo通过变得更像人来超越‘深蓝’”这样为人津津乐道的桥段。

在接下来的内容中，我们将尝试用MCTS解决一个朴素的寻路问题：

在 $n\times m$ 的网格中有若干障碍物，每步可以从某一点的上下左右方向中的一个迈出一步。给出起点 $(f x, f y)$ 和终点 $(t x, t y)$ ，求路径。

数据结构与定义

由于起止点已知，基于贪心策略，期望每步尽量能减少和终点的距离是朴素的。然而考虑到解的不确定性，不能通过简单贪心来解决问题，仍然需要对整个网格进行搜索。

定义网格为n*m的矩阵，f与t为起止点的坐标，b为障碍物列表。

内部用grid保存可通行情况（是否有障碍物），visited表示地图中的该点是否已被试探过，trails记录当前可供试探的节点列表，path记录节点由哪个节点展开而来，在最后生成路径时反向遍历以得出最终路径。

# 用 Monte Carlo Tree Search解决 寻路问题
# by 1mlightyears@gmail.com
# 20210215
class MCTS:
    def setMap(self,
               n: int = 15,
               m: int = 15,
               f: tuple = (0, 0),
               t: tuple = (14, 14),
               b: list = [],
               sleep: float = 0.1,
               nograph: bool = False):
        """
        地图声明部分。
        n,m(int):地图长宽。
        f,t(tuple[int,int]):起点与终点。
        b(list[tuple[int,int]]):地图中不可通行的障碍物。
        sleep(float):控制试探间隔时间。
        nograph(bool):不显示可视化窗口。
        """

        self.grid = np.array([[False for j in range(m)] for i in range(n)])
        self.n = n
        self.m = m
        self.f = f
        self.t = t
        self.sleep = sleep
        self.nograph = nograph
        for i in b:
            self.grid[i[0]][i[1]] = True
        seed = int(time())
        np.random.seed(seed)

		# log
        print(f"地图={n}*{m} 从{f}到{t}\n障碍:{b}")
        print(f"随机种子:{seed}")
        # 可视化部分
        if not self.nograph:
            for i in range(n):
                for j in range(m):
                    self.X.append(i)
                    self.Y.append(j)
            self.C = [[0 for j in range(m)] for i in range(n)]
            se.set()
            plt.ion()

寻路算法的基本假设

因为一条具体的路线是由路线上的每一点各自的决策组成的，每点各自又是一个具体的状态，所以这是一个在状态空间中的搜索。因此选择概率匹配为MCTS的搜索策略。³

不同于复杂的AlphaGo的决策树，寻路问题的搜索树并没有复杂的“交换棋手”的需求，因此没有在决策之间切换的必要，可以暂时不实现反向传播的过程。寻路问题必定会搜索到一个解（把“无解”也当成一个解），因此不需要限定搜索时间。

在当前某一状态下选择展开的新节点时，最常采用的是上限置信度区间算法(Upper Confidence Bound, UCB)。⁴然而，朴素的UCB算法处理有状态转移（从地图上的一点移动到下一点）的问题时效率相当低下——每个节点初始的被选取概率都相等意味着新节点等概率地被试探，搜索将花费大量时间在“拓宽视野”而不是“向终点前进”上。称这种情况为“算法收敛较慢”。

因此，本实现通过MCTS寻路的遍历策略是：

优先试探更优的节点。在这个简单的模型中，优先试探离终点更近的节点。
如果一个节点更优（离终点更近），那么这个节点将具有更高的权重，以在将来的试探中更有可能被选中，反之亦然。
显然，如果将优秀节点的权重设为无限大，那么这就是一个朴素的贪心算法。在某些复杂的场景下，用来估计节点情况的估计函数可能会很复杂。
由1.，到终点距离相当的节点应当有相近的权值，到终点距离不同的节点权重应显著不同。
这是显然的，由于贪心思想的要求，距离终点更近的节点若要被优先试探必须有更高的权值，而由于候选列表的长度随试探次数增加而变化，更优节点需要有显著高的权值。

需要重申的是上述两点并非通过MCTS解决寻路问题的一般要求，更非全部要求。随着地图具体结构和特点的不同可以采取不同的假设，对于本实现所解决的简单地图来说，采用贴近贪心算法的假设是容易收敛的。否则，如果去掉2.的“显著不同”条件，那么算法将更倾向于均等地在候选列表中寻找下一个试探节点——而不是向着“正确的方向”找下一个试探节点，在极端情况下则又变回了UCB。（节点的权值差距不能无限制扩大，见结果分析部分）

因此，搜索算法可按如下思路设计：

初始化试探节点表trails，标记起点，设置路线记录表path；
从trails中加权随机选取一个节点进行试探；
从该节点试探其周围节点，按上述两点计算其权重；
删除该节点（因为它已不能产生新路径）
重复1，直到试探到终点，或已无节点可以试探。

权值计算

作为蒙特卡洛算法，在搜索算法的具体实现中需要加权随机产生一个试探节点。为满足基本假设的2.条件，最简单直接的实现即是将子节点的权值设为父节点的一定倍数，以在不同代节点中积累出数量级差距，从而实现更优节点的“显著高的权值”。

def __Ins(self, x, y, fr: node = node()):
        """
        将新试探点插入trails。
        x(int),y(int):新试探点的坐标；
        fr(node):新试探点由哪个点发展而来（父节点）。
        新试探点的具体权重由旧点和它到终点的期望决定。
        """
        if (x, y) == self.t:
            return True
        sign = (abs(self.t[0] - x) + abs(self.t[1] - y)) - \
            (abs(self.t[0] - fr.x) + abs(self.t[1] - fr.y))
        weight = fr.weight * self.factor ** sign
        self.trails.append(node(x, y, weight))

然而，实际使用中该算法存在权值爆炸的问题。

为使得不同代间产生显著差异，子节点的权重是由父节点简单乘除一个因子factor产生的。在路径较长时，靠近终点的权值将比起点附近权值高数十个数量级（取决于具体的factor选取）。

为解决这一问题，采用类似于科学计数法的指数形式存储具体权值：
$W=p\times b^{l}\tag{1}$
其中 $W$ 为上文中的原始权重weight， $p$ 为因数； $b$ 为底数base， $l$ 为指数level。

这种存储方法不仅可以解决权重爆炸的问题，还可以利用多引入的参数实现阶段性搜索（见下文）。

改进后的权值计算算法实现：

def __Ins(self, x, y, fr: node = node()):
        """
        将新试探点插入trails。
        x(int),y(int):新试探点的坐标；
        fr(node):新试探点由哪个点发展而来。
        新试探点的具体权重由旧点和它到终点的期望决定。
        """
        if (x, y) == self.t:
            return True
        sign = (abs(self.t[0] - x) + abs(self.t[1] - y)) - \
            (abs(self.t[0] - fr.x) + abs(self.t[1] - fr.y))

        # 权重函数
        # 1. 离终点越近的节点权重越高，离起点越近的函数权值越低
        # 2. 距终点距离相当的节点权重相当，相邻节点需要有明显差距
        # 3. 为防止权重爆炸，使用 p=weight*base^level 的科学计数法模式记录权值，显然weight<base
        # 4. 利用3.，每次只将level最大的那些节点的weight加入权重候选，除非节点数少于threshold个/level==0
        # 5. log(base,p)=ln p/ln base

        ln_weight = np.log(fr.weight)

        level = fr.level
        weight = fr.weight * self.factor ** sign
        if weight>self.base:
            level += 1
            weight /= self.base
        if weight < 1:
            level -= 1
            weight *= self.base

        self.trails.append(node(x, y, weight, level))
        self.visited[x][y] = True
        return False

当然，其实也可以使用简单的双精度实现，而且还可以获得更高的performance；但是哪怕是double的 $±10E308 \pm10E308$ 数据范围也只能满足大约 $25\times25$ 的地图规模，对于诸如 $100\times100$ 以上的地图采取上述科学计数法更加通用。⁵

改进后的权值存储和加权随机策略

在trails中存储的每个节点如下定义：

class node:
    def __init__(self,
        x: int = 0,
        y: int = 0,
        weight: float = 1,
        level: int = 0
    ):
        """
        trails中的节点的数据结构。
        """
        self.x, self.y, self.weight, self.level = x, y, weight, level

此处以及下文的weight均为原weight的底数部分（即式 $(1)$ 中的 $p$ ）。
由于指数level（也就是定义式 $(1)$ 中的 $l$ ）的引入，搜索算法的2.步骤可以不在整个trails中随机选取，这是因为：到终点不同距离的节点，其权值有显著差异，则部分权值较低的节点可以忽略。因为它们实际被取到的概率极低；且若要将它们加入随机选取，则在计算时高权重节点的权值又将变得极大（权值爆炸）。

在最终实现中，每次试探前先构建随机选取表choices，由完整的trails中level最大的节点组成。对于被选入choices中的节点，每次加权随机选取一个试探，权值为各节点的weight。

为防止choices中的元素过少，设置threshold为choices中节点个数的下限；若choices中的节点数不足threshold个，则扩大选取范围，将trails中level次大的节点也加入choices，依此类推直到choices中的节点个数超过threshold个，或所有节点均加入choices（此时choices实质上即等于trails）。

MCTS搜索部分实现如下：

def Search(self,
           threshold: float = -float("inf"),
           factor: float = -float("inf"),
           base: float = -float("inf")
          ):
        """
        搜索路径。
        """
        if threshold > -float("inf"):
            self.threshold = threshold
        if factor > -float("inf"):
            self.factor = factor
        if base > -float("inf"):
            self.base = base

        # 初始化:试探节点表trails，设置起点，设置路线记录表path
        self.trails = [node(self.f[0], self.f[1])]
        self.visited[self.f[0]][self.f[1]] = True
        self.path = [[None for j in range(self.m)] for i in range(self.n)]
        no = 0
        print(f"base:{self.base} factor:{self.factor} threshold:{self.threshold}")
        print("===训练开始===")

        while len(self.trails) > 0:
            # 当前level,初始值为当前最大的level
            now_level = max(self.trails, key=lambda x: x.level).level

            # 加入权重候选的节点序号表choices及其权重表weights
            choices = [i for i in range(len(self.trails)) if self.trails[i].level == now_level]
            weights = np.array([self.trails[i].weight for i in choices])

            # 如果序号表数量不够threshold则将更低一层的也加入进来，如果还是不够则继续扩大范围
            # 直至满足threshold的数量
            while (len(choices) < self.threshold) and (now_level > 0):
                now_level -= 1
                ex = [i for i in range(len(self.trails))
                      if self.trails[i].level == now_level]
                weights = np.concatenate((weights * self.base,
                                         np.array([self.trails[i].weight for i in ex])))
                choices.extend(ex)

            #随机抽取一个节点进行试探
            unitary = sum(weights)
            r = np.random.choice(choices, size=1, p=[i / unitary for i in weights])[0]
            no += 1
            print(
                f"{no}:搜索{(self.trails[r].x,self.trails[r].y)},偏好{self.trails[r].weight/unitary:.2f}({self.trails[r].weight:.2f}/{unitary:.2f}) , ", end="")
            x, y = self.trails[r].x, self.trails[r].y

            # ←
            if (x > 0) and (not self.visited[x - 1][y]):
                self.path[x - 1][y] = (x, y)
                print(f" ↓ 增加{(x-1,y)} ", end="")
                if self.__Ins(x - 1, y, self.trails[r]):
                    break

            # ↓
            if (y > 0) and (not self.visited[x][y - 1]):
                self.path[x][y - 1] = (x, y)
                print(f" ← 增加{(x,y-1)} ", end="")
                if self.__Ins(x, y - 1, self.trails[r]):
                    break

            # →
            if (x + 1 < self.n) and (not self.visited[x + 1][y]):
                self.path[x + 1][y] = (x, y)
                print(f" ↑ 增加{(x+1,y)} ", end="")
                if self.__Ins(x + 1, y, self.trails[r]):
                    break

            # ↑
            if (y + 1 < self.m) and (not self.visited[x][y + 1]):
                self.path[x][y + 1] = (x, y)
                print(f" → 增加{(x,y+1)} ", end="")
                if self.__Ins(x, y + 1, self.trails[r]):
                    break

            # 删去这个已试探节点
            del self.trails[r]
            print(f"队列长度:{len(self.trails)}")

            if not self.nograph:
                self.__frame()
                plt.gca().remove()
                plt.scatter(self.X, self.Y, s=6000 // self.n //
                            self.m, c=self.C, cmap='cubehelix')
                plt.pause(self.sleep)

至此算法部分基本完成。添加了地图生成、命令行接口、可视化、logging等的完整demo，请查看GitHub上的完整源代码。

测试运行

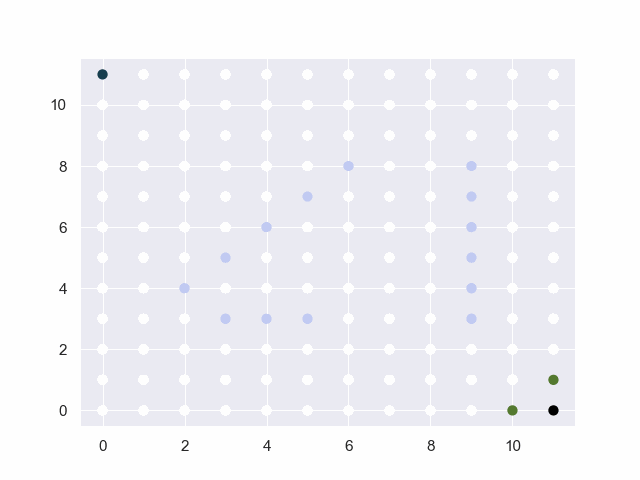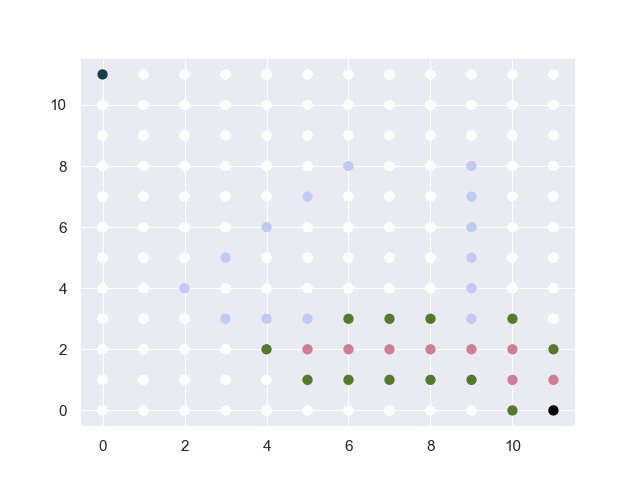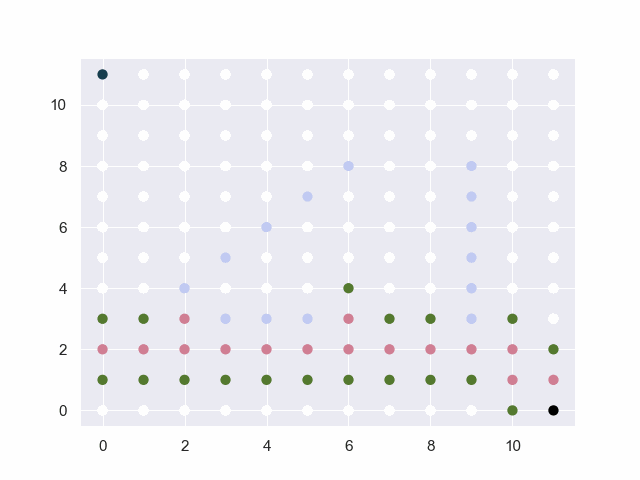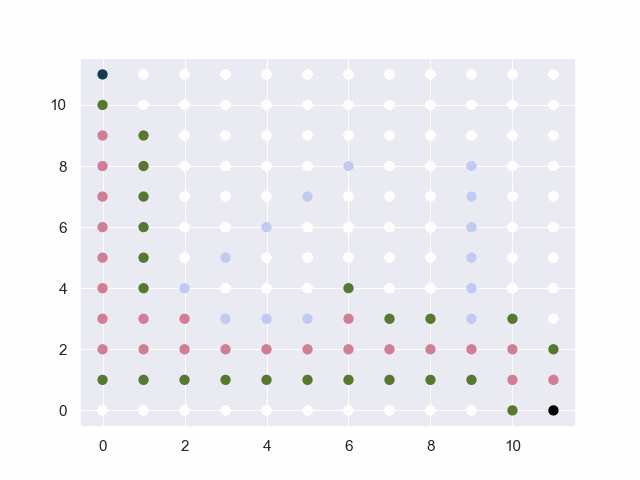
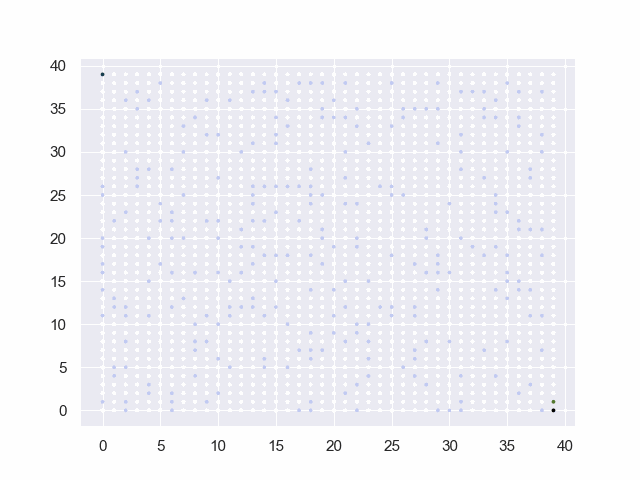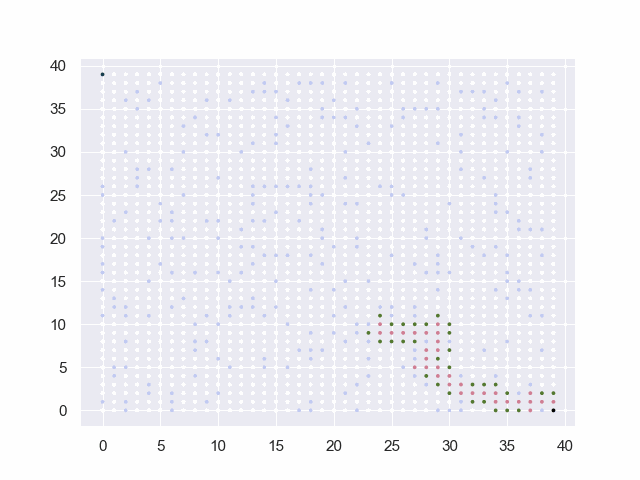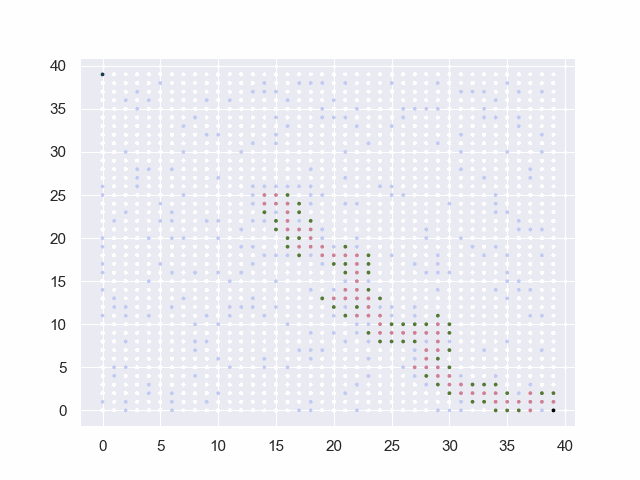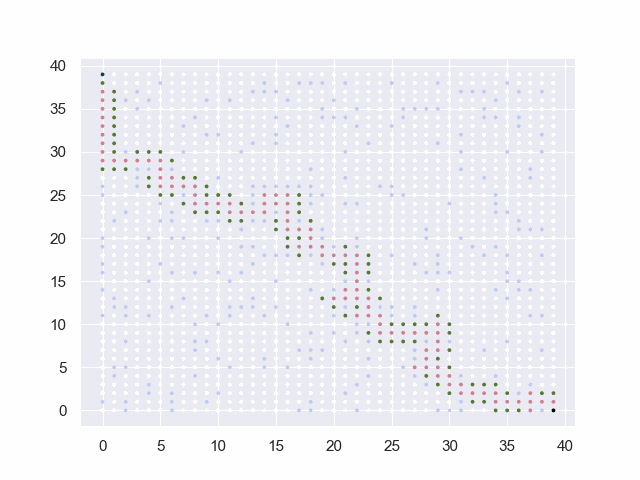
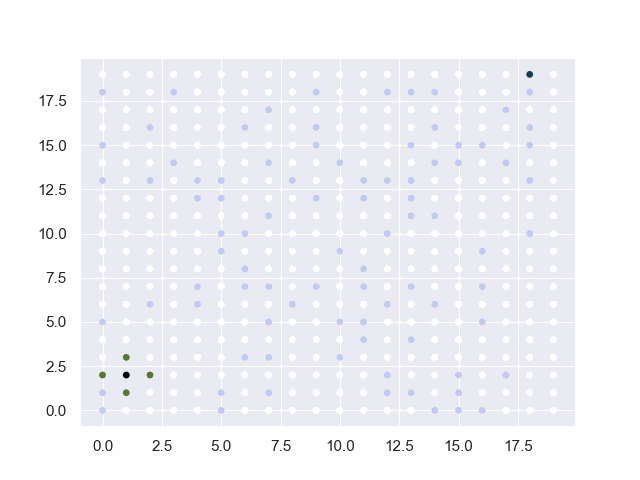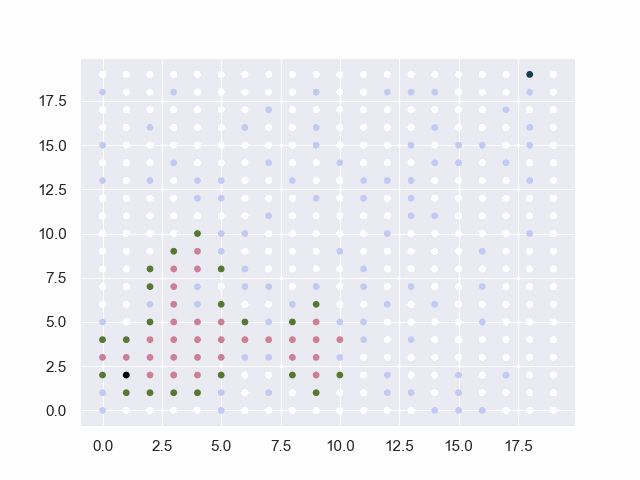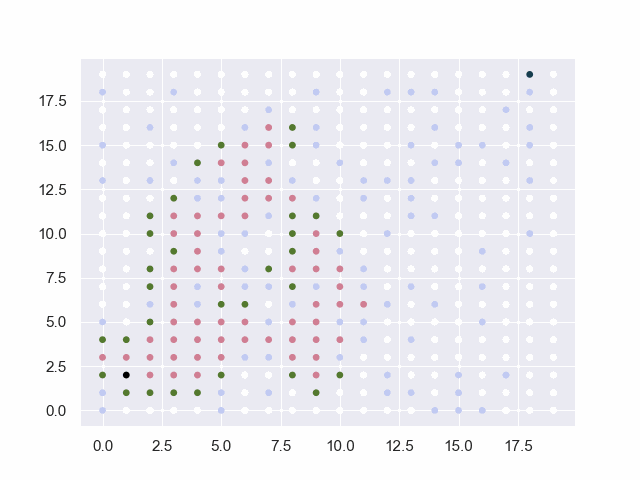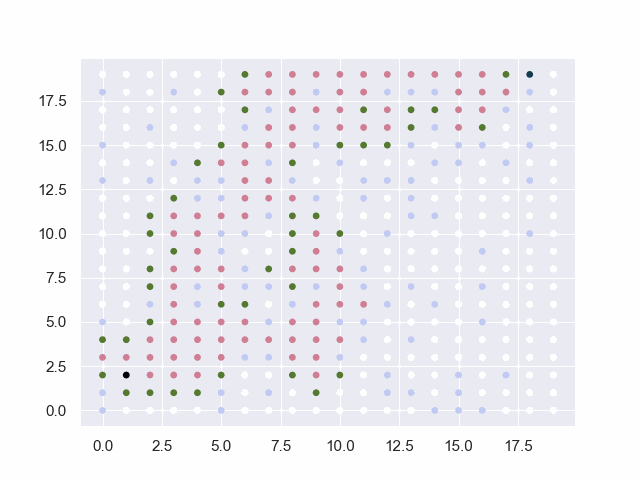
图中的黑点表示起止点，白点为可通行路径，淡蓝点为障碍物，红点为已试探的节点，绿点为trails中的候选点。

地图=10*10
从(0, 0)到(9, 9)
障碍:[(2, 2), (3, 2), (4, 2), (5, 2), (6, 2), (5, 4), (5, 5), (5, 6), (5, 7), (5, 8), (5, 9)]
base:30 factor:4 threshold:4

测试1

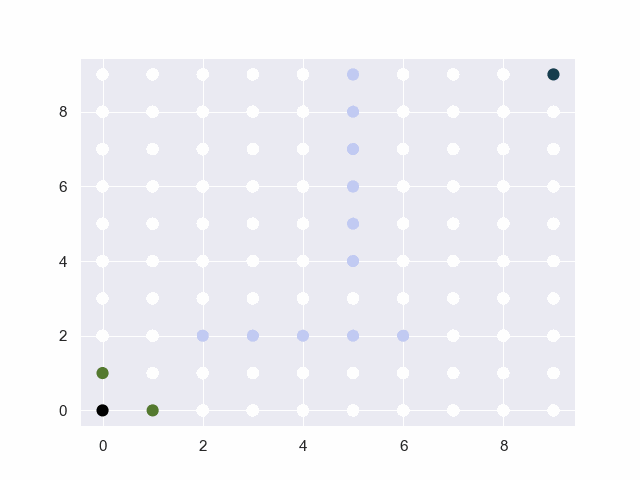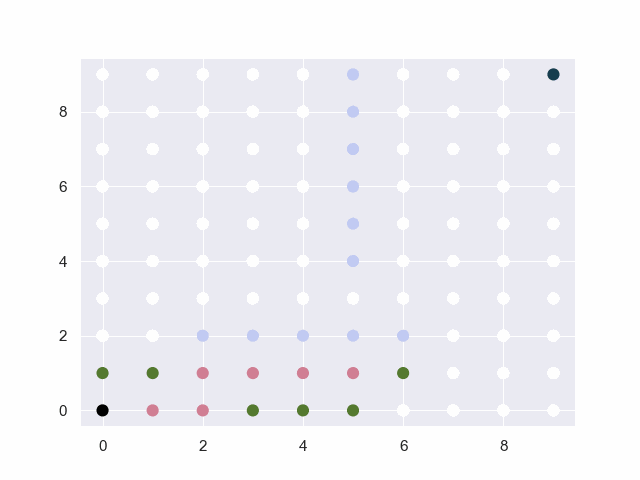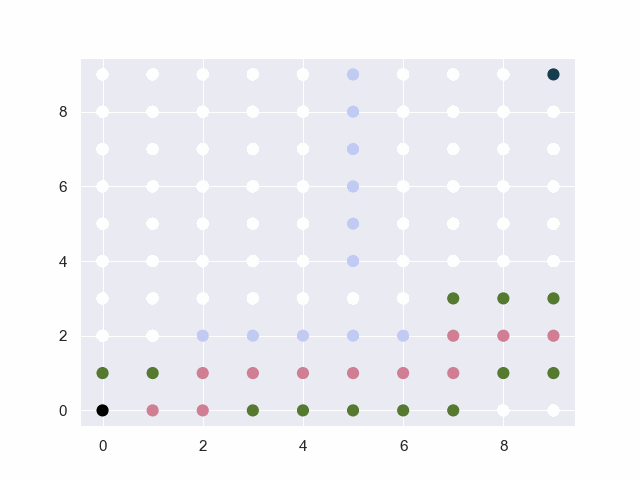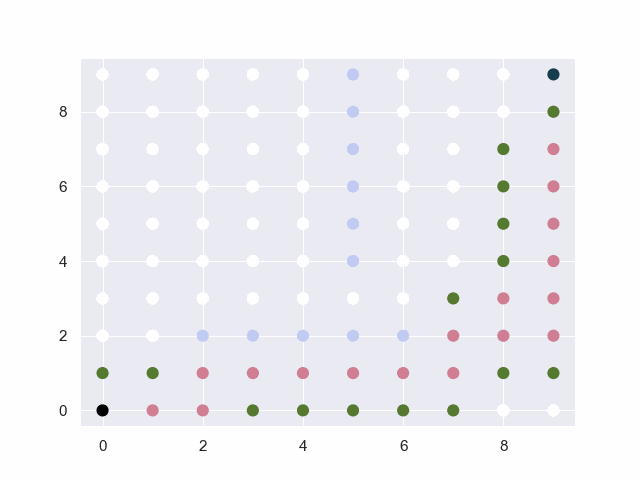
地图=12*12
从(11, 0)到(0, 11)
障碍:[(2, 4), (3, 5), (4, 6), (5, 7), (6, 8), (9, 3), (9, 4), (9, 5), (9, 6), (9, 7), (9, 8), (3, 3), (4, 3), (5, 3)]
base:30 factor:4 threshold:4

测试2

地图=15*15
从(0, 13)到(14, 1)
障碍:[(1, 3), (2, 5), (3, 8), (5, 5), (4, 5), (9, 2), (6, 1), (6, 2), (6, 3), (6, 4), (7, 11), (9, 13), (12, 12), (6, 8), (9, 4), (13, 5), (12, 5), (11, 5), (11, 6), (11, 7), (2, 11), (4, 10), (1, 9), (1, 11), (1, 13), (13, 2), (14, 2), (10, 0), (12, 8), (13, 13)]

测试3

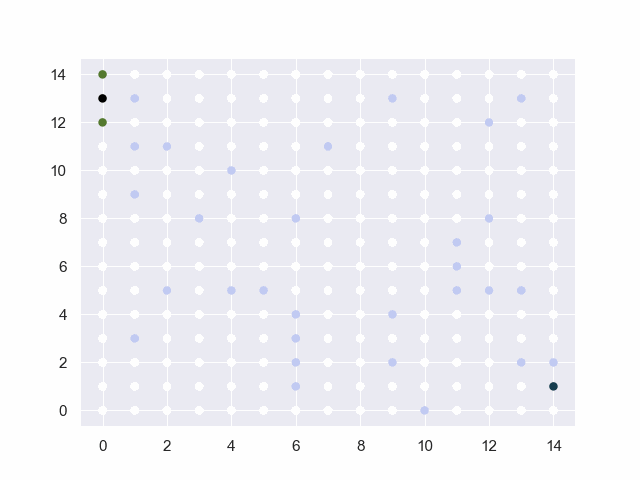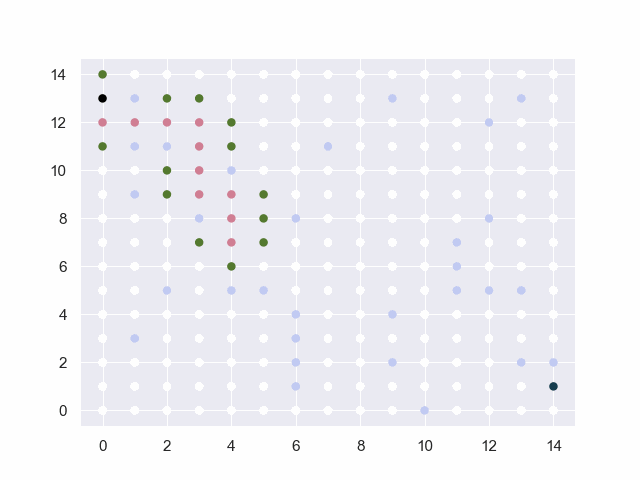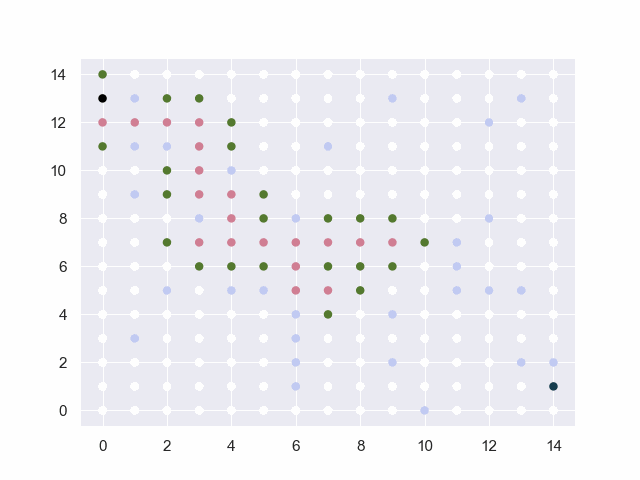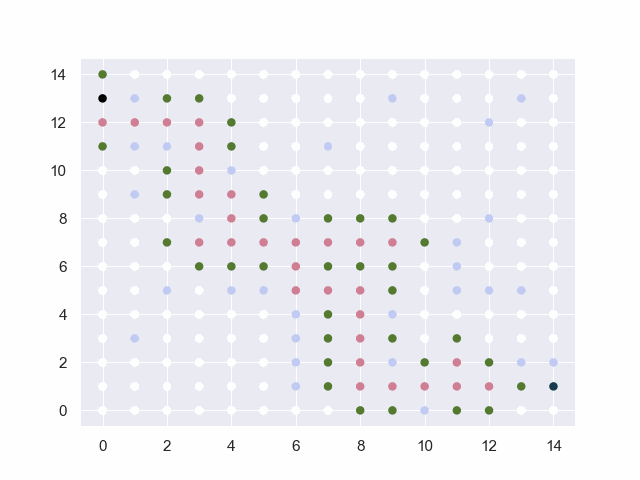
地图=40*40
从(39, 0)到(0, 39)
障碍:[(13, 13), (21, 27), (14, 18), (2, 36), (18, 25), … (省略295项)]
base:50 factor:8 threshold:6

测试4
一个factor较小的例子：

地图=20*20
从(1, 2)到(18, 19)
障碍::[(16, 0), (6, 16), (15, 14), (18, 10), (12, 1), … (省略95项)]
base:50 factor:1.5 threshold:5

测试5

可以看出，搜索出路径的收敛速度变慢，明显在枝杈道路上花费了更多试探次数。由于随机性的引入，重复相同的初始条件基本不可能完全复现；但是在大量重复实验下收敛速度/解的平均长度会受到factor等参数的影响。

结果分析

该算法效率较传统的Dijkstra、A*算法低，且得出的结果可能并不是最佳（最短）路径。虽然在得出路径方面，MCTS可能在总的试探数上占优（较少），但每试探一个节点的代价较大。
关于时间复杂度 $O$ ：一般来说由于随机带来的解的不确定性，难以直接衡量一个蒙特卡洛算法的时间复杂度。
同时， threshold，factor，base这些参数也会影响解的质量和收敛速度。
考虑全局最优解为 $q$ 步的一个场景：
$\bar{E}=\sum_{i=q}^{\infty}P(\mathrm{path}=i)\cdot i\\ 其中\bar{E}为解的步数期望，P(\mathrm{path}=i)为解的步数为i的概率，\\ 假设对于每个节点可选路径都充分多，且平均都有一半的路径是朝着终点方向“前进”的，\\那么，记\mathrm{factor}=f，在最优路径上的第m步，其被选择的概率p(m)可表示为:\\p(m)=\frac{\frac{1}{2}\bar{r}\cdot f^m}{\frac{1}{2}\bar{r}\cdot f^m+\frac{1}{2}\bar{r}\cdot f^{m-1}+\bar{r}\cdot f^{m-2}+...+\bar{r}\cdot f+\bar{r}+\frac{1}{2}\bar{r}/f}\\ =\frac{\frac{1}{2}\bar{r}\cdot f^m}{\sum_{j=1}^{m}\frac{1}{2}\bar{r}\cdot f^j+\sum_{k=-1}^{m-2}\frac{1}{2}\bar{r}\cdot f^k}\\ 其中\bar{r}为每个节点的平均决策数（平均可选路径数，相对于1充分大）。\\这样就可以将P表示出来:\\ P(\mathrm{path}=q)=\prod_{i=1}^{q} p(i)\\ 如果其中走了一步岔路，则最终解即为q+1步，相当于：\\ P(\mathrm{path}=q+1)=P(\mathrm{path}=q)\cdot \frac{p'(x)}{p(x)}\\ 上式表示在第x步走岔的、总步数为q+1的路径被选取的概率。\\ 将在第x步走岔的概率p'(x)表示出来：\\ p'(x)=\frac{\frac{1}{2}\bar{r}\cdot f^{x-1}}{\sum_{j=1}^{x}\frac{1}{2}\bar{r}\cdot f^j+\sum_{k=-1}^{x-2}\frac{1}{2}\bar{r}\cdot f^k}\\ 显然，\frac{p'(x)}{p(x)}=\frac{1}{f}<1，故在忽略走岔对P中分母项的影响的情况下，\\对于走岔0\sim t_0步的情况，有：\\ \bar{E}=\sum_{t=0}^{t_0}(\prod_{i=1}^{q} p(i)\cdot\frac{1}{f^{t}}\cdot (i+t))\\ \sum P=\prod_{i=1}^{q}(p(i)\cdot\frac{f^{t_0+1}-1}{f^{t_0}(f-1)})\\ 其中t_0表示走岔了t_0步（忽略走岔对于p表达式分母的影响）\\显然，当t_0\to\infty时，相当于解遍历整个地图，那样一定会寻找到路径；\\ 当t_0为0时，相当于解为最优解q。\\ 因此，可大致认为f（即\mathrm{factor}）影响解的收敛速度，\\ \mathrm{level}和\mathrm{base}联合起到截断的作用，通过忽略高阶项增加效率。$
然而，factor并不是越大越好，因为估计函数给出的结果并不一定可信（不能在不知道最优解的情况下确保走在最优解的道路上），故应对factor设置一定的值，确保MCTS落在朴素贪心DFS和BFS之间的合适位置，才能最大化MCTS的效果。对于此最佳factor值的选择，可以通过对于一定类型地图进行训练来进行。
作为启发式的搜索方法，MCTS是一个解决决策问题的“超人”——通过核实的评估函数的设计，它可以以类似于人的思维方式，用计算机的运算速度解决一系列决策问题。
也因此，它在能给出和人类解相近的解。这一特点适宜于解决诸如扫地机器人寻路等开放型问题。相比之下，其他解决开放型问题的寻路算法如D*算法⁶在复杂度和实现难度上不落下风（可参考GitHub上D*算法的实现：pshafer的Java实现，Daniel-beard的Java实现以及fengyunxiren的Python实现）。
如果考虑到计算时间复杂度时所用的假设，那么MCTS也将适用于解决一些非离散网格结构地图的寻路。在这些地图上A*将变得比较无力⁷，而MCTS只需简单修改即可按照同一逻辑完成寻路。
接上，地图如果带有特殊格子（如，代价较大倾向于回避的地形，分时可通过的地形，条件触发的障碍物，多精灵寻路等）也会影响寻路，主要是估计函数的可信度将降低。
熟悉war3的朋友肯定对下面这玩意不陌生，这个东西也会影响寻路
注意到path的定义会使得每个节点只有唯一前趋，如果一个节点被试探就意味着被完全扩展，接下来的试探中它将变得和障碍物一样无法通行。
这直接使得后续的路径优化变得极为困难：在某些极端的场合下，即使一个解被试探出来且有优化空间，它也可能由于周围被已试探节点包围而难以被优化。
要解决这一问题需要一种更适合反向传播的数据结构。

总结

MCTS可以解决寻路问题，其优势在于，一个设计良好的估计函数可以让MCTS最大限度模拟人类的路径规划得出贴近人类思维的路径，这点在地图情况未知的开放型寻路中较有优势；其算法可以朴素地实现，但因每步的计算量较A*大，故其效率相较于传统的A*更低。
因此，MCTS适用于复杂地理环境寻路、动态环境寻路、未知环境寻路（如机器人寻路）等场合，不适用于高效率寻路、已知路径点寻路、静态寻路等场合。

https://gameinstitute.qq.com/community/detail/100044 ↩︎
关于A*算法的介绍与实现 ↩︎
David Silver, Reinforcement Learning[M], Para. 9 ↩︎
机器学习A-Z～置信区间上界算法 Upper Confidence Bound or UCB ↩︎
GCC支持四精度的浮点数__float128。该数据类型的表示范围为 $±10E4932 \pm 10E4932$ ，可以表示最接近0的数是 $3.36 E - 4932$ 。但是由于大多数现有的CPU无法直接对__float128运算，因此实际的__float128运算将被拆分成多条CPU指令，所耗时间也远高于double。见https://blog.csdn.net/liyuanbhu/article/details/7935321 ↩︎
关于D*算法的介绍与实现 ↩︎
当尺寸超过1024*1024网格之后，普通的A*就将变得吃力了，而一些巨大的高精度的地图想达到这一尺寸相当容易，这时就需要对A*进行改进。这个实现采用了分治法减少了网格的总数，不过也可以使用MCTS直接解决原始问题。 ↩︎