拓扑排序的原理及其实现

最新推荐文章于 2023-05-06 23:09:02 发布

风先生

最新推荐文章于 2023-05-06 23:09:02 发布

阅读量867

点赞数

分类专栏： c/c++ 算法

本文链接：https://blog.csdn.net/qq_30490125/article/details/53046138

版权

c/c++ 同时被 2 个专栏收录

69 篇文章 0 订阅

订阅专栏

算法

14 篇文章 0 订阅

订阅专栏

这里要从一道题目开始说起

这里写图片描述

题目大意：我们的系统现在有一连串的事务需要处理，但事务之间存在依赖性，问我们的事务应该以怎样的顺序进行处理。
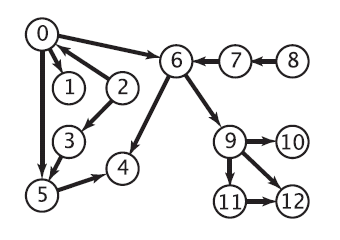
第一行读入两个整数，节点总数m，依赖项的个数n；接下来读入n行数据，每行数据：A size BCDE，表示BCDE完成以后才能处理A，size表示接下来的节点个数

输入：
13 11
1 1 0
5 2 0 3
0 1 2
3 1 2
4 2 5 6
6 2 0 7
7 1 8
9 1 6
10 1 9
11 1 9
12 2 9 11

拓扑排序的定义及其充要条件

定义：将有向图中的顶点以线性方式进行排序。即对于任何连接自顶点u到顶点v的有向边uv，在最后的排序结果中，顶点u总是在顶点v的前面。

简单来说，我们以选课为例，假如我想选修机器学习，选课系统判断我从未选修过数据结构和算法，选课失败。这里的数据结构和算法就相当与u0和u1，而这里的机器学习就相当于v。
但我很想选修机器学习，所以我只能先选修数据结构和算法，等这两个选修完成以后，再取选修机器学习。这个过程以算法的形式描述出来的结果就被称为拓扑排序。

假如因为系统问题，学校的选课系统在我选修数据结构的时候要求我已经选修机器学习。这个时候选课无法继续进行，因为它中间存在互相依赖的关系，从而无法确定谁先谁后。在有向图中，这种情况被描述为存在环路。因此，一个有向图能被拓扑排序的充要条件就是它是一个有向无环图(DAG：Directed Acyclic Graph)。

拓扑排序的具体实现

Kahn算法O(N + E)

维基百科上关于Kahn算法的伪码描述：

L← Empty list that will contain the sorted elements
S ← Set of all nodes with no incoming edges
while S is non-empty do
remove a node n from S
insert n into L
foreach node m with an edge e from nto m do
remove edge e from thegraph
ifm has no other incoming edges then
insert m into S
if graph has edges then
return error (graph has at least onecycle)
else
return L (a topologically sortedorder)

思路非常简单，我们首先找到所有入度为０的节点，当如到队列当中，每次输出一个入度为０的节点，紧接着循环遍历由该节点引出的所有边对应的节点，将该节点的入度减１，如果该顶点的入度在减去１之后为0，那么也将这个顶点放到入度为0的集合中。然后继续从队列中取出一个顶点，知道队列为空。
在这个过程中记录遍历的节点个数，如果输出的节点个数等于输入的节点个数，此时我们已经完成了拓扑排序；如果少于输入的节点个数，说明图中至少存在一条环路。

细节代码：

#include <map>
#include <queue>
#include <iostream>
using namespace std;
bool solve()
{
    int n;
    int nodeSize;
    cin >>nodeSize >> n;
    int cur;
    int rely;
    int numRely;
    vector<int> numChild(nodeSize, 0);//每个节点的入度个数
    vector<vector<int> > reverseMap(nodeSize);//出度表
    queue<int> input0;
    vector<int> result;
    for (int i = 0; i < n; ++i)
    {
        cin >> cur >> numRely;
        numChild[cur] = numRely;
        for(int j = 0; j < numRely; ++j)
        {
            cin >> rely;
            reverseMap[rely].push_back(cur);
        }
    }
    for(int i = 0; i < nodeSize; ++i)
        if(numChild[i] == 0)
            input0.push(i);
    int count = 0;
    while(!input0.empty())
    {
        ++count;
        cur = input0.front();input0.pop();
        result.push_back(cur);
        for(int i = 0; i < reverseMap[cur].size(); ++i)
        {
            rely = reverseMap[cur][i];
            if(--numChild[rely] == 0)
                input0.push(rely);
        }
    }
    if(count != nodeSize)
    {
        cout<< count<< endl;
        return false;
    }
    for(int i = 0; i < count; ++i)
        cout<< result[i];
    return true;
}
int main()
{
    if(!solve())
        cout<<"circle exist"<<endl;
    return 0;
}

output: 2 8 0 3 7 1 5 6 4 9 10 11 12

基于DFS的拓扑排序算法O(N + E)

维基百科上的伪码描述：

L ← Empty list that will contain the sorted nodes
S ← Set of all nodes with no outgoing edges
for each node n in S do
visit(n)

function visit(node n)
if n has not been visited yet then
mark n as visited
for each node m with an edgefrom m to ndo
visit(m)
add n to

算法成立的简单解释：参考树的后序遍历（每个出度为０的节点作为根），假定节点输出以后就会消失，那么此刻这棵树的打印的每个节点都可以保证自己没有孩子节点。

Detail:
考虑任意的边v->w，当调用dfs(v)的时候，有如下三种情况：

dfs(w)还没有被调用，即w还没有被mark，此时会调用dfs(w)，然后当dfs(w)返回之后，dfs(v)才会返回
dfs(w)已经被调用并返回了，即w已经被mark
dfs(w)已经被调用未返回，在之后的调用中出现调用dfs(v)的情况

很明显，第三种情况的出现意味着有向图中出现了环路，从而该图就不是一个有向无环图(DAG)，而我们已经知道，非有向无环图是不能被拓扑排序的。而无论是第一种情况还是第二种情况，w都会在v之前被输出。

细节代码：

#include <vector>
#include <iostream>
using namespace std;
vector<int> result;
void dfsVisit(vector<vector<int> >& mapin, vector<bool>& visited, int cur)
{
    visited[cur] = 1;
    for(int i = 0; i < mapin[cur].size(); ++i)
    {
        if(!visited[mapin[cur][i]])
            dfsVisit(mapin, visited, mapin[cur][i]);
    }
    result.push_back(cur);
}
bool dfs(vector<vector<int> >& mapin, vector<bool>& visited, int cur)
{
    visited[cur] = 1;
    for(int i = 0; i < mapin[cur].size(); ++i)
    {
        if(!visited[mapin[cur][i]])
            dfs(mapin, visited, mapin[cur][i]);
        else
            return false;
    }
    return true;
}
bool DAG(vector<vector<int> >& mapin, vector<int>& outGoing)
{
    int nodeSize = mapin.size();
    for(int i = 0; i < outGoing.size(); ++i)
    {
        vector<bool> visited(nodeSize, 0);
        if(!dfs(mapin, visited, outGoing[i]))
            return false;
    }
    return true;
}
bool solve()
{
    int n;
    int nodeSize;
    cin >>nodeSize >> n;
    int cur;
    int rely;
    int numRely;
    vector<bool> visited(nodeSize, 0);//访问标记
    vector<int> outGoing(nodeSize, 0);//每个节点的出度个数
    vector<vector<int> > mapin(nodeSize);//入度表
    vector<int> outGoing0;
    for (int i = 0; i < n; ++i)
    {
        cin >> cur >> numRely;
        for(int j = 0; j < numRely; ++j)
        {
            cin >> rely;
            mapin[cur].push_back(rely);
            outGoing[rely]++;
        }
    }
    for(int i = 0; i < nodeSize; ++i)
        if(outGoing[i] == 0)
            outGoing0.push_back(i);
    if(!DAG(mapin, outGoing0))
        return false;
    for(int i = 0; i < outGoing0.size(); ++i)
        dfsVisit(mapin, visited, outGoing0[i]); 

    for(int i = 0; i < nodeSize; ++i)
        cout<< result[i]<< " ";
    return true;
}
int main()
{
    if(!solve())
        cout<< "circle exist"<< endl;
    return 0;
}

output: 2 0 1 3 5 8 7 6 4 9 10 11 12

两种实现算法的总结：

对于基于DFS的算法，是根据出度表构建的，从出度为０的节点递归。Kahn算法，是根据入度表构建的，从入度为0的节点开始遍历。

Kahn算法不需要检测图为DAG，如果图为DAG，那么在出度为0的集合为空之后，遍历的节点个数少于图中节点的总数，这就说明了图中存在环路。而基于DFS的算法需要首先确定图为DAG，当然也能够做出适当调整，让环路的检测和拓扑排序同时进行，毕竟环路检测也能够在DFS的基础上进行。
二者的复杂度均为O(V+E)

环路的检测和拓扑排序同时进行:

#include <vector>
#include <iostream>
using namespace std;
vector<int> result;
bool dfs(vector<vector<int> >& mapin, vector<bool>& visited, vector<bool>& DAGValid, int cur)
{
    visited[cur] = 1;
    DAGValid[cur] = 1;
    for(int i = 0; i < mapin[cur].size(); ++i)
    {
        if(!visited[mapin[cur][i]])
            dfs(mapin, visited, DAGValid, mapin[cur][i]);
        else if(DAGValid[mapin[cur][i]])
            return false;
    }
    result.push_back(cur);
}
bool solve()
{
    int n;
    int nodeSize;
    cin >>nodeSize >> n;
    int cur;
    int rely;
    int numRely;
    vector<bool> visited(nodeSize, 0);//访问标记
    vector<int> outGoing(nodeSize, 0);//每个节点的出度个数
    vector<vector<int> > mapin(nodeSize);//入度表
    vector<int> outGoing0;
    for (int i = 0; i < n; ++i)
    {
        cin >> cur >> numRely;
        for(int j = 0; j < numRely; ++j)
        {
            cin >> rely;
            mapin[cur].push_back(rely);
            outGoing[rely]++;
        }
    }
    for(int i = 0; i < nodeSize; ++i)
        if(outGoing[i] == 0)
            outGoing0.push_back(i);

    for(int i = 0; i < outGoing0.size(); ++i)
    {
        vector<bool> DAGValid(nodeSize, 0);//判断环存在的数组
        dfs(mapin, visited, DAGValid, outGoing0[i]);    
    }

    for(int i = 0; i < nodeSize; ++i)
        cout<< result[i]<< endl;
    return true;
}
int main()
{
    if(!solve())
        cout<< "circle exist"<< endl;
    return 0;
}

行文思路参考：http://blog.csdn.net/dm_vincent/article/details/7714519

风先生

关注

0
点赞
踩
1

收藏

觉得还不错? 一键收藏
0
评论
拓扑排序的原理及其实现

这里要从一道题目开始说起题目大意：我们的系统现在有一连串的事务需要处理，但事务之间存在依赖性，问我们的事务应该以怎样的顺序进行处理。第一行读入两个整数，节点总数m，依赖项的个数n；接下来读入n行数据，每行数据：A size BCDE，表示BCDE完成以后才能处理A，size表示接下来的节点个数输入： 13 11 1 1 0 5 2 0 3 0 1 2 3 1 2 4 2 5 6 6
复制链接

扫一扫

专栏目录