凸优化知识博大精深，学习一下便于方便理解机器学习算法中的优化原理，学习了一点皮毛总结一下。
引用七月在线算法班程博士的凸优化初步（统一论）
想说明白凸优化是什么就要先清楚最优化问题，了解了最优化问题我们会恍然大悟为什么会是凸优化。
优化问题
很多机器学习中的问题都可以被看做成一个优化问题，也就是找最优解，接下来先看一个例子
求解一个线性方程组：
x
1
+
2
x
2
=
0
x_1+2x_2=0
x1+2x2=0
2
x
1
+
x
2
=
1
2x_1+x_2=1
2x1+x2=1
3
x
1
+
2
x
2
=
1
3x_1+2x_2=1
3x1+2x2=1
这个问题就可以转化成以下形式
m
i
n
x
1
,
x
2
(
x
1
+
2
x
2
−
0
)
2
+
(
2
x
1
+
x
2
−
1
)
2
+
(
3
x
1
+
2
x
2
−
1
)
2
min_{x_1,x_2}(x_1+2x_2-0)^2+(2x_1+x_2-1)^2+(3x_1+2x_2-1)^2
minx1,x2(x1+2x2−0)2+(2x1+x2−1)2+(3x1+2x2−1)2
这里为什么有平方呢是因为每个式子存在正负方向，因此加上平方就可以让上式>=0进行求解。这种求解思路其实就是最小二乘法的思想。
无约束优化问题
我们在实际上遇到的问题通常是涉及到多元特征的问题，因此当我们把问题转化成求解最小值的形式为
m
i
n
f
(
x
)
minf(x)
minf(x)
x
∈
R
n
x \in \mathbb{R}^n
x∈Rn
所谓优化就是找到极小值点
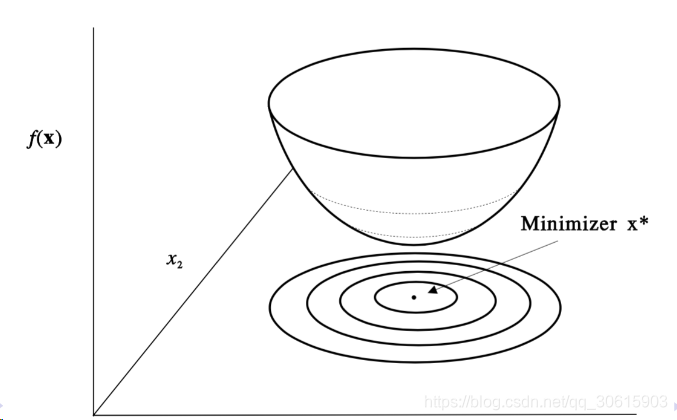上图中的底面投影就是等值线，在优化问题中经常遇到的。上图是简化的理想问题，但是在真实问题中我们遇到的问题通常不会这么简单，大多数情况都是下图这样复杂的曲线的优化问题。
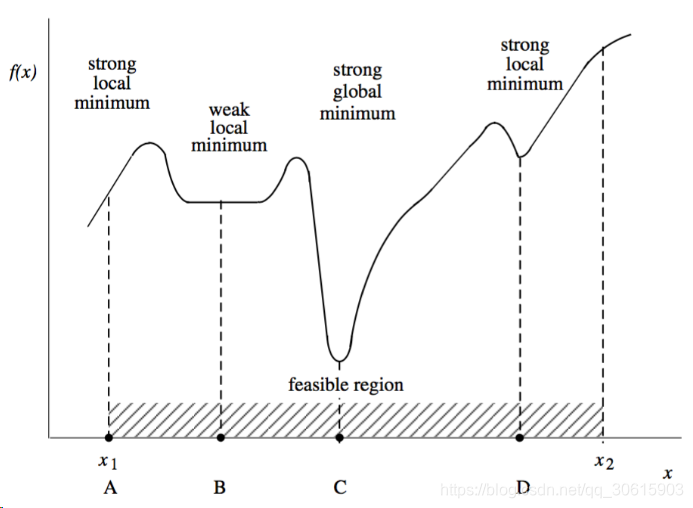我们可以看到上图中存在着很多局部最优点，只有c点才是全局最优点。当然还有一种情况是最尴尬的如图所示
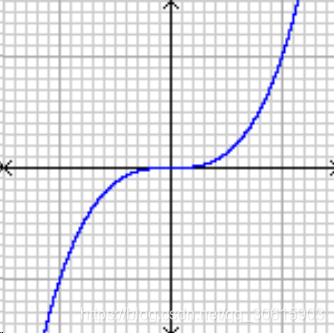在该点处他的一阶导数为零但却不是最优点。
一阶导数和梯度
f
′
(
x
)
=
▽
f
(
X
)
=
[
∂
f
(
X
)
∂
x
1
∂
f
(
X
)
∂
x
2
.
.
∂
f
(
X
)
∂
x
n
]
f'(x) = ▽f(X)= \begin{bmatrix} \frac{∂f(X)}{∂x_1} \\ \frac{∂f(X)}{∂x_2} \\.\\.\\ \frac{∂f(X)}{∂x_n} \\ \end{bmatrix}
f′(x)=▽f(X)=⎣⎢⎢⎢⎢⎢⎡∂x1∂f(X)∂x2∂f(X)..∂xn∂f(X)⎦⎥⎥⎥⎥⎥⎤
二阶导数和Hessian矩阵
f
′
′
(
x
)
=
▽
2
f
(
X
)
=
[
∂
2
f
(
X
)
∂
x
1
2
∂
2
f
(
X
)
∂
x
1
∂
x
2
.
.
∂
2
f
(
X
)
∂
x
1
∂
x
n
∂
2
f
(
X
)
∂
x
2
∂
x
1
∂
2
f
(
X
)
∂
x
2
2
.
.
∂
2
f
(
X
)
∂
x
n
∂
x
1
∂
2
f
(
X
)
∂
x
n
2
]
f''(x)= ▽^2f(X)=\begin{bmatrix} \frac{∂^2f(X)}{∂x_1^2} & \frac{∂^2f(X)}{∂x_1∂x_2} & . &. &\frac{∂^2f(X)}{∂x_1∂x_n}\\ \frac{∂^2f(X)}{∂x_2∂x_1} & \frac{∂^2f(X)}{∂x_2^2}\\.\\.\\ \frac{∂^2f(X)}{∂x_n∂x_1}& & & &\frac{∂^2f(X)}{∂x_n^2} \\ \end{bmatrix}
f′′(x)=▽2f(X)=⎣⎢⎢⎢⎢⎢⎢⎡∂x12∂2f(X)∂x2∂x1∂2f(X)..∂xn∂x1∂2f(X)∂x1∂x2∂2f(X)∂x22∂2f(X)..∂x1∂xn∂2f(X)∂xn2∂2f(X)⎦⎥⎥⎥⎥⎥⎥⎤
泰勒展开式
f
(
x
k
+
δ
)
≈
f
(
x
k
)
+
f
′
(
x
k
)
δ
+
1
2
f
′
′
(
x
k
)
δ
2
f(x_k+\delta) \approx f(x_k) + f'(x_k)\delta+\frac{1}{2}f''(x_k)\delta^2
f(xk+δ)≈f(xk)+f′(xk)δ+21f′′(xk)δ2
x
k
+
δ
x_k+\delta
xk+δ表示的是
x
k
x_k
xk附近的点通过泰勒展开式我们可以知道当
f
′
(
x
)
=
0
f'(x)=0
f′(x)=0时可以用
f
′
′
(
x
)
f''(x)
f′′(x)的正负来判断当前点是否为极值点，对应到Hessian矩阵上就是是否正定，正定即为极小值点，不定为鞍点，要是等于零就得通过三阶导数继续展开来看了。
求解方法
无约束条件优化方法
迭代法
1 选择一个初始点，设置一个convergence tolerance ε，计数k=0
2 确定一个搜索方向
d
k
d_k
dk
3 确定步长也就是学习率
α
k
α_k
αk 更新
x
k
+
1
=
x
k
+
α
k
d
k
x_{k+1}=x_k+α_kd_k
xk+1=xk+αkdk
4 如果
‖
α
k
d
k
‖
<
ε
‖α_kd_k‖<ε
‖αkdk‖<ε，则停止输出解
x
k
+
1
x_{k+1}
xk+1；否则继续重复迭代。
深度下降法（最速下降法）中的搜索方向
d
k
=
−
∇
f
(
x
)
d_k=−∇f(x)
dk=−∇f(x)，该方法时在等值线上的表现如下图，优点在于每一步都可以向着好的方向下降，但缺点就是太慢了。这里每次下降的轨迹是正交的
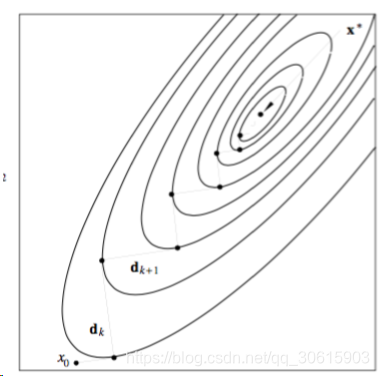
牛顿法在于搜索方向
d
k
=
−
(
∇
2
f
(
x
k
)
)
−
1
∇
f
(
x
k
)
d_k=−(∇^2f(x_k))^{−1}∇f(x_k)
dk=−(∇2f(xk))−1∇f(xk)引入了二阶导数，如果Hessian不可逆的话，会作适当修正来修正梯度下降的方向，通常为
▽
2
f
(
x
k
+
β
I
)
1
+
β
\frac{▽^2f(x_k+\beta I)}{1+\beta}
1+β▽2f(xk+βI)他没有一阶导数那么传统，他可能一步就收敛到最优解，但同时也可能往坏的方向下降。有利有弊。
二者对比
最速下降法：下降曲线为z字型，方向为负梯度方向，每次按部就班的下降一次
牛顿法：不是负梯度，受到二阶导数Hessian矩阵的正定性影响。但Hessian按矩阵不一定可逆因此存在很多优化算法，可以使用拟牛顿等其他的方式。
凸集
上述方法能够对于无约束条件的最优化问题解出局部最优解，但我们并不能确定这个解是全局最优的。因此这引出凸集的概念。那么什么是凸集呢，概念很简单，如果一个集合内的任意两点之间的连线都在集合内的话那么这个集合就是凸集，用数学符号表示：一个集合
C
∈
R
n
C∈ \mathbb{R}^n
C∈Rn是凸的，则对于任意的x,y∈C，有
θ
x
+
(
1
−
θ
)
y
∈
C
θx+(1−θ)y∈C
θx+(1−θ)y∈C其中
0
≤
θ
≤
1
0≤θ≤1
0≤θ≤1
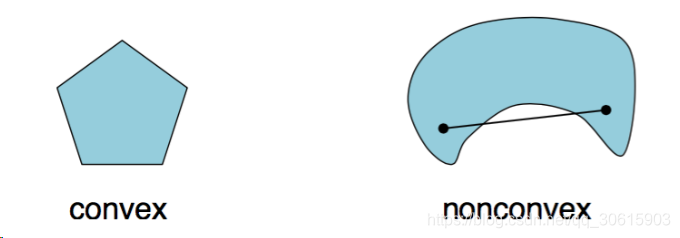
常见的凸集
- 超平面（是不是瞬间想到SVM，但这属于带约束条件的下次讲）
- 半空间
- 多面体
- 欧式球
- 椭球
凸函数
一个函数f: R n → R \mathbb{R}^n→\mathbb{R} Rn→R被称为凸函数，如果
- dom(f)(f的定义域)是凸集
- 对于任何x,y∈dom(f) 和 0≤θ≤1
f ( θ x + ( 1 − θ ) y ) ≤ θ f ( x ) + ( 1 − θ ) f ( y ) f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y) f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y)
也可以理解成凸函数的水平集就是凸集。
我们说了这么多为什么要引出凸函数呢，因为凸函数有一个很棒的性质在凸函数里解出的局部最优就是全局最优解，是不是一下子恍然大悟，这就是为什么凸优化叫做凸优化了。优化方法可找到局部最优，而凸集来说就是全局最优，老师说了一句话很经典，如果我们把一个问题转换成凸函数了，那么这个问题就已经gameover了。
一阶导数充要条件：
f
(
x
1
)
≥
f
(
x
)
+
∇
T
f
(
x
)
(
x
1
−
x
)
f(x_1)≥f(x)+∇Tf(x)(x_1−x)
f(x1)≥f(x)+∇Tf(x)(x1−x)这是一阶泰勒展开式，对于所有x1,x均成立。
若此时二阶可导且Hessian矩阵正定则是该函数为凸函数的充要条件。
为什么凸函数的局部最优就是全局最优
这里可以使用反证法，我们先假设存在一个局部最优点
x
0
x_0
x0，既然是局部最优那一定存在
x
∗
x_*
x∗使得
f
(
x
∗
)
<
f
(
x
0
)
f(x_*)<f(x_0)
f(x∗)<f(x0)也就是说存在比局部最优还小的点。
此时结合凸函数的定义，存在
δ
\delta
δ
f
(
δ
x
∗
+
(
1
−
δ
)
x
0
)
≤
δ
f
(
x
∗
)
+
(
1
−
δ
)
f
(
x
0
)
f( \delta x_∗+(1−\delta)x_0)≤ \delta f(x_∗)+(1−\delta)f(x_0)
f(δx∗+(1−δ)x0)≤δf(x∗)+(1−δ)f(x0)
δ
\delta
δ 是0到1之间无限趋近于零的，
δ
x
∗
+
(
1
−
δ
)
x
0
\delta x_∗+(1−\delta)x_0
δx∗+(1−δ)x0 就会无限趋近于
x
0
x_0
x0, 但是函数在这个点的值又比
f
(
x
0
)
f(x_0)
f(x0) 小，所以假设矛盾，则证明该点不存在，即局部最优点就是全局最优点。
1431
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
