多阶段决策求最优解----动态规划（Dynamic Programming）

引例1：最短路径求解

求A–E的最短路程距离
对于一般的问题我们可以采取深度优先搜索来找出每一个路径的长度再整体比较；或者使用贪心，从局部最优解推导出整体最优解。
但是对于深搜，如果这个图很大，那么效率将是非常低的；
对于贪心，如果出现有两条路径的距离是一样的，那么这一步的贪心就无法进行下去；而且局部最优到最后并不一定是全局最优，比如一条路径是5 1 1，另一条路径是3 5 6（图只在第一个口除有分岔口）
那我们该如何处理呢？
其实，距离这个问题，我们可以把这个图分成四个阶段分别为A-B,B-C,C-D,D-E，我们要把每一个最小的距离求出来，再与前面一阶段进行匹配，分别找出每个节点的最短路径。最终就能得到最优解。
解决：
我们用F(x)来表示x到E的最短距离，每次计算F(x)记为该节点到下一节点的最短路径。那么我们可以得到状态转移方程为F(x)=min{F(y) + x到y的距离}（注意这个可能有多个，因为对于x所处的状态，节点不一定只有一个）。

从中有三个重要的概念：
1.阶段
问题的过程被分成若干个互相联系的部分，我们称为阶段，以便按一定的次序求解。
2.状态
某一阶段的出发位置称为状态，通常一个阶段包含若干个状态，如第三层又f(C1),f(C2),f(C3),f(C4)状态。
3.决策
对问题的处理中作出的每种选择的行动就是决策，即从该阶段的每个状态出发，通过一次选择性行动移至下一个阶段的相应状态。

引例2：数塔问题

一个由非负数组成的三角形，第一行只有一个数，除了最下行之外每个数的左下方和右下方各有个数，从第一行的数开始，每次可以选择向左下或是向右下走一格，一直走到最下行，把沿途经过的数全部加起来。如何走才能使得这个和尽量大？

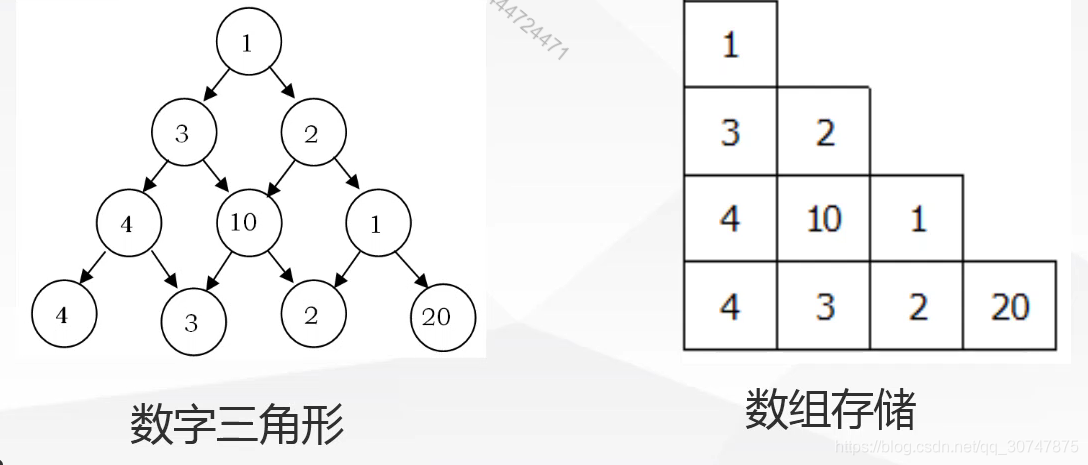
首先，在上面的引例1中已经说明不能使用贪心（如果3下面的4是1000，这个题就做错了）。这个题目由于数据比较少，我们可以利用搜索来做。

搜索的代码实现

#include <bits/stdc++.h>
using namespace std;
int n, arr[110][110], sum, max_ = -1;

void dfs(int x, int y, int sum) {
	if (x <= n) {
		/*if (x == n) { //说明到底了
			if (sum > max_)
				max_ = sum;
		}*/
		max_ = max(max_, sum);//这样写也可以 更简洁但是效率稍微低一点
		dfs(x + 1, y, sum + arr[x + 1][y]);
		dfs(x + 1, y + 1, sum + arr[x + 1][y + 1]);
	}
}

int main() {
	scanf("%d", &n);
	for (int i = 1; i <= n; ++i) {
		for (int j = 1; j <= i; ++j) {
			cin >> arr[i][j];
		}
	}
	dfs(1, 1, arr[1][1]);
	cout << max_;
}

但是很明显，这样搜索太慢了，时间复杂度为O(2ⁿ)，当n比较大时，这个复杂度是接受不了的，所以导致大数据类型过不了。

于是采取动态规划来求解

动态规划的思路

本题的动态规划有两种思路，一种是从下向上的递推，把每一步的最大值都向上加，最后得到的dp[1][1]就是最大值，这种方法的复杂度下降到了O(n²)。另一种是从上而下递归，由状态转移方程：d[i][j]=arr[i][j]+max(d[i+1][j],d[i+1][j+1])，可以逐步得出每个状态下的最大值，可以发现此方法的复杂度也是O(2ⁿ)。因为递归的过程中有大量重复计算的数，导致重复性的动作太多太多，从而降低了速度；而递推过程中通过建立一个新的dp数组，把所有计算过的值都存入dp数组中，那么就减去了很多重复的计算，从而达到简化复杂度。
递归的过程一般是伴有回溯的，而回溯的过程中有些东西一定会被重复计算的，所以单纯的递归算法在大数据面前没有什么太大的简化作用。

递推代码 空间换时间

#include <bits/stdc++.h>
using namespace std;
int dp[1000][1000], n, arr[1000][1000];
void fun() {
	for (int i = 1; i <= n; ++i) {
		dp[n][i] = arr[n][i];
	}
	for (int i = n - 1; i >= 1; --i) {
		for (int j = 1; j <= i; ++j) { //每行有i个元素
			dp[i][j] = arr[i][j] + max(dp[i + 1][j], dp[i + 1][j + 1]);
		}
	}
}

int main() {
	scanf("%d", &n);
	for (int i = 1; i <= n; ++i) {
		for (int j = 1; j <= i; ++j) {
			cin >> arr[i][j];
		}
	}
	fun();
	cout << dp[1][1];
}

递归代码

#include <bits/stdc++.h>
using namespace std;
int arr[1000][1000], n;

//从x y点开始走到最后一层经过的数字和的最大值
int dp(int x, int y) {
	if (x < n)
		return arr[x][y] + max(dp(x + 1, y), dp(x + 1, y + 1));
	else
		return  arr[x][y];
}

int main() {
	scanf("%d", &n);
	for (int i = 1; i <= n; ++i) {
		for (int j = 1; j <= i; ++j) {
			cin >> arr[i][j];
		}
	}
	cout << dp(1, 1);
}

记忆化搜索 用于降低递归的复杂度

求解每个点的值，先判断这个点有没有求解过，求解过的话我就不再去求解了.

#include <bits/stdc++.h>
using namespace std;
int arr[1000][1000], n, dp[1000][1000]; 
int f3(int x, int y) {
	if (x < n) {
		if (dp[x][y] == -1) {
			dp[x][y] = arr[x][y] + max(f3(x + 1, y), f3(x + 1, y + 1));//先存储起来
			return dp[x][y];//再return
		} else {
			return dp[x][y];
		}
	} else {
		return arr[x][y];
	}
}

int main() {
	scanf("%d", &n);
	for (int i = 1; i <= n; ++i) {
		for (int j = 1; j <= i; ++j) {
			cin >> arr[i][j];
		}
	}
	memset(dp, -1, sizeof(dp)); 
	//memset(数组名,初始值,sizeof)是将数组的值初始化初始值只能是0或-1
	f3(1, 1);
	cout << dp[1][1] << endl;//或者cout<<f3(1,1)也可
}

动态规划理论小结

基本思想：划分阶段（子问题），确定状态及状态间的转移关系，使用递推或者记忆化搜素。
状态定义：用问题的某些特征参数描述一个子问题。在上题中用d[i][j]表示以格子(i,j)为根的子三角形的最大和。在很多时候，状态描述的细微差别引起算法的不同。
状态转移方程：即状态值之间的递推关系。这个方程通常需要考虑两个部分：一是递推的顺序，而是递归的边界（也是递推的起点）。
从直接递归和后两种方法可以看出，动态规划的优越体现在重叠子问题的求解上面。

动态规划的性质

子问题重叠性质：每次产生的子问题并不一定是新问题，在直接使用递归的时候会造成重复子问题的多次计算。
最优化子结构性质：包含的子问题也是最优解。
无后效性：未来与后续无关。比如上面树的遍历，就可以往回走，没有任何影响。

是用动态规划的前提：能花分阶段、符合最优化原理、具备无后效性。

动态规划的优势

1、动态规划比穷举具有较小的计算次数
从上面的数塔问题可以看书，动态规划的时间复杂度明显更优秀。
2、递归需要非常大的栈空间，而动态规划的递推法不需要栈空间；使用记忆化搜素哦可以有效地减小计算量。

解决问题的基本特征

1、动态规划一般解决最值（最优，最大，最小，最长…）等问题；
2、动态规划解决的问题是可以分阶段的；
3、动态规划解决的问题必须包含最优子结构，即可以由（n-1）的最有推出n的最优；

该算法的四步骤

1、划分阶段：按照问题的特征，将问题分为若干个阶段，阶段需有序或可排序。
2、确定状态和状态变量：将问题发展到每一个阶段的状态表示出来。
3、确定决策并写出状态转移方程
4、寻找边界条件：与递归的终点、递推的起点有关系。