SVM——对偶支持向量机

SVM——对偶支持向量机
1.之前谈了线性支持向量机的具体求解过程，可以化简到这个式子：

这个式子带有条件的最小化问题可以用二次规划方式来求解。
2.现在有一种新的方式来对此公式继续化简，对于上面的式子，我们可以定义一个拉格朗日多项式，即：


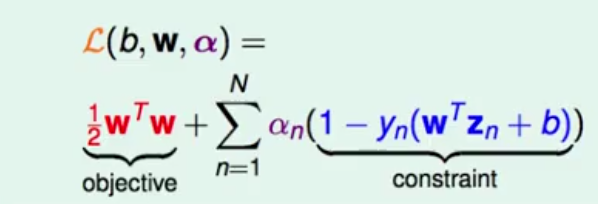
那么SVM就可以写成仙最大化拉格朗日多项式，再最小化。为什么可以这样写呢，因为如果b跟w不满足第一张图中的条件，那么再最大化是alpha会重点内容趋于无限大；如果b跟w满足条件，alpha就会等于0，那么max那一项的结果就自然等于图一中的那一项。那么我们在minimize括号中的最大化拉格朗日项的时候会自动忽略区域无穷大，也就是不满足图一中条件的那一项。所以此时，上次讲的线性支持向量机现在可以转化为这样：

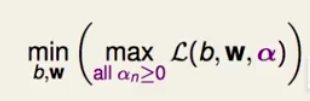
3.因为式中的alpah是挑选的最大的那一项再做得最小化，所以当我们随便选取alpha不最大化时会有这个式子：

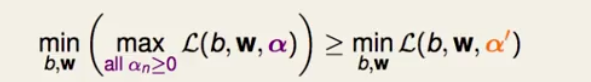
因为任何的α^‘都会小于等左边的式子，所以即使是取最大值同样会满足，这个就是拉格朗日对偶问题：

4.那么现在求解SVM是要通过右边的式子，但是右边的式子不太好解，且括号里面要取最大，如果是求解左边那个式子就会相对简单点了，因为min到了里面，我们可以用梯度下降法直接求出最优b跟w。但问题在于是大于等于，并不是等于，所以二者并不等价，那么此时会出现一个强对偶关系：

当式子满足这三条关系的时候，就可以自动等价了，第一条是求解问题是凸函数，第二个是有解，也就是样本线性可分的。
5.那么现在现在变成了解决拉格朗日对偶问题：

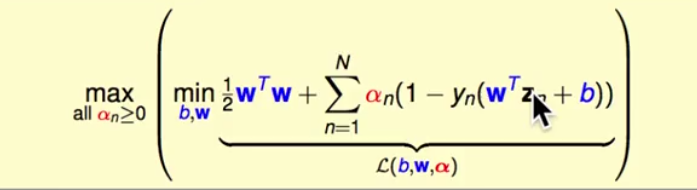
此时对于w没有任何条件，非常自由。先看括号中的最小化问题，之前谈到过解决这种问题的方法，就是梯度下降法，梯度下降法的核心就是让对于所有变量参数的偏导都等于0，那么就可以说找到了最优解，所以此时式子可以继续化简，首先对b求偏导可以得出：

紧接着对Wi求偏导：

得出这两个条件后，我们可以继续将拉格朗日对偶问题继续化简为：

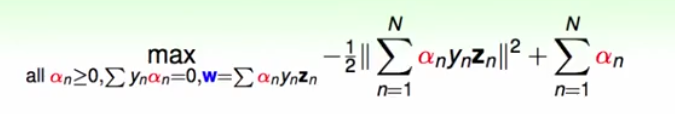
6.此时的问题就是解决max后面关于alpha的多项书的问题，这就是简化版的拉格朗日对偶问题。根据这个公式就可以求解出最好的alpha，并且根据KKT理论，只有当满足这些条件时，对偶问题的化简才会成立：

此时，我们将alpha大于0的点叫做support vector，就是支持向量，支持向量就是离分类面最近的线，跟之前不一样的是要alpha大于0，而不仅仅是在分类边界上了：

7.求解出最好的alpha后我们就可以通过对偶问题的三个条件来求解我们真正想要的w跟b了，它们才是决定分类面的重要参数，在算的时候也只用support vector来计算b跟w，其他的点不用管：

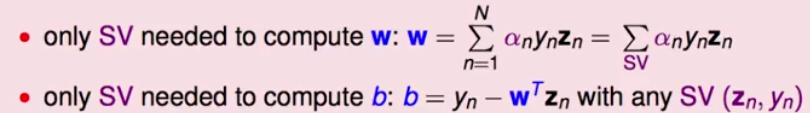
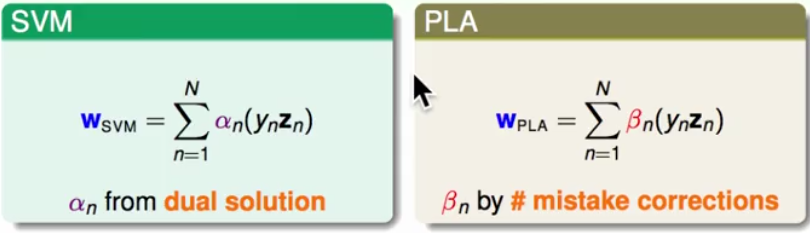
8.那么此时可以发现，SVM和PLA(感知机)有点类似，SVM是原始资料在support vector上的一个线性组合，而PLA是原始资料在犯错的点上的线性组合，PLA就是在每次犯错之后进行相加，所以总结来说，SVM就是用support vector来表现，而PLA用犯错的点来表现：