今天介绍一下Neural NetWork,都是一下个人理解,认真看的话看懂肯定不是问题。个人微信公众号:计算机金融阅读。欢迎关注。
1.首先介绍一下神经网络的基本组成,从左边开始,那些x就是输入样本点所包含的特征,然后经过第一层的w权重,得出第二层神经元(图中圆圈表示神经元)的输入值,在经过一个激活函数将输入值S转化为输出值X,这里的激活函数可以选用不同的函数,在吴恩达机器学习视频中的激活函数为sigmoid函数,这里台湾大学讲的是tanh函数,依次类推得出最后一层的输出结果,从而达到分类或者回归的效果。
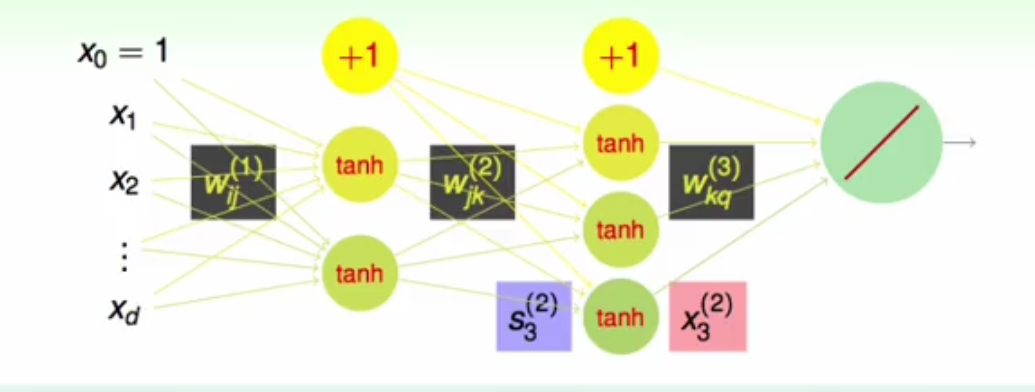
2.那么我们怎么通过这些输出,去训练学习这些权重W呢?当然这些权重需要将输出的误差降到最低,令en代表最小平方误差,那么同样应用梯度下降法求解en对于每一个w的偏导,即可进行优化。
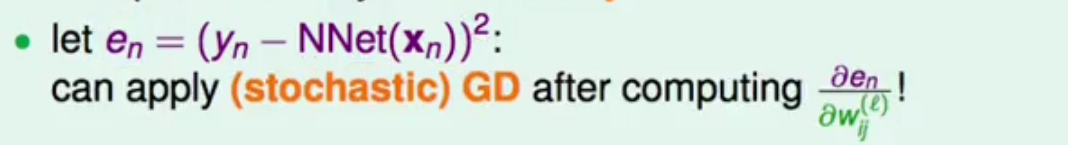
3.从最后一层L层开始计算化简,其中yn为样本的标签值,NNet(xn)为通过正向传播得出的值,也可以写作S1(假设最后只有一个输出值),那么S1又可以写成第L-1层的输出值X与第L层W之间乘积之和。

4.那么通常来说,误差en对于最后一层的w的偏导就可以根据3中的en表达式来写。en对w求偏导,可以写成先对s求偏导,在乘以s对w求偏导;其中en对s求偏导根据3很好求出(如写入所示),s再对w求偏导求出来就是x,那么特殊的最后一层的偏导就求出来了。那么一般的前面那些层的w的偏导应该怎么求呢?同样也可以写成en先对s求偏导,s再对w求偏导;其中s对w求出来肯定是x,而前面的一项en对中间层的s偏导很难求出,那么现在关键就是求出en对s的一般形式。

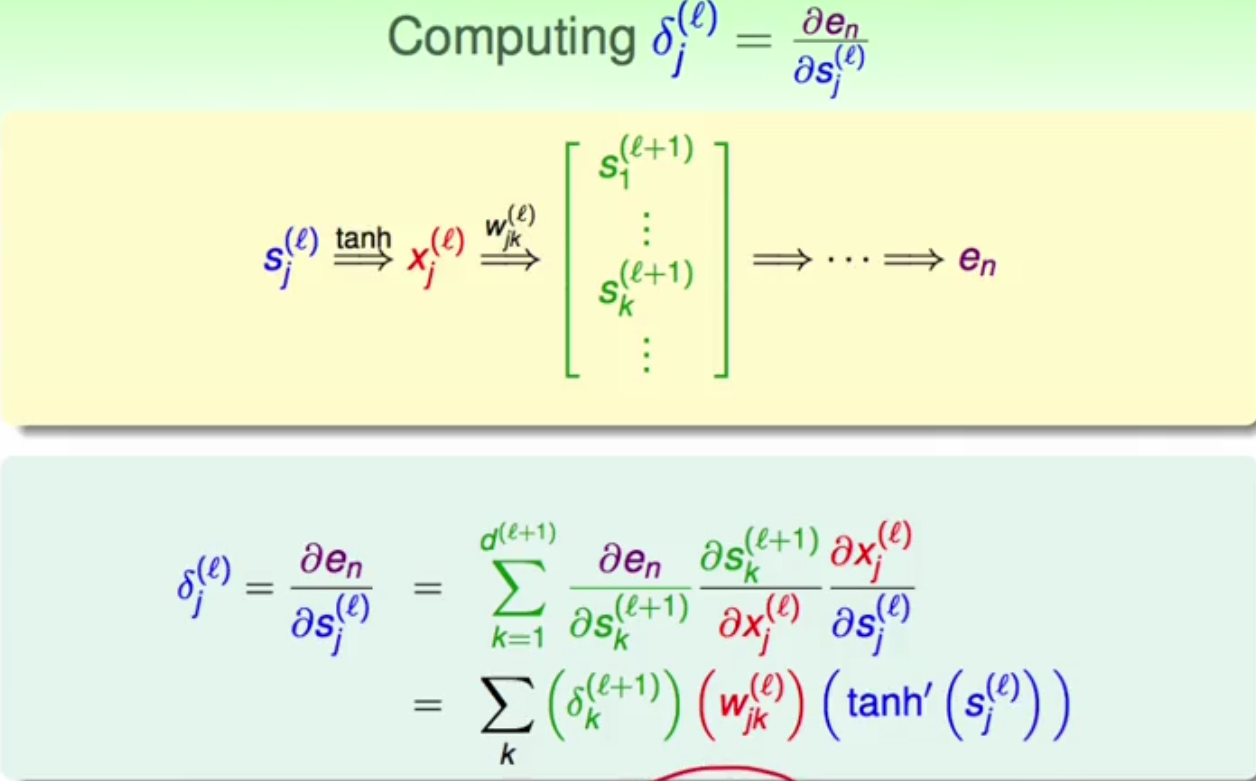
5.如下图所示,先看一下s是如何影响最后的en的。首先第l层的s经过激励函数tanh得出第l层的输出x,在经过第l层的w加权得出第l+1层的输入值s,在经过同样的步骤正向传播得出最后的误差en。所以en对第l层s的偏导就可以写为:en对第l+1层的s的偏导,由于第l+1层有d个s,所以要进行加和,在乘以s对第l层的x进行求偏导,在乘以第l层的x对第l层的s求偏导。那么很容易发现,第一项就是滴l+1层的delta,第二项为w,第三项即对tanh中的s进行求导。
6.那么整个训练神经网络的过程就可以概括为以下步骤:随机选择N个样本点中的一个样本进行前向传播,得出每一层的x以及s,在通过上面已经提到的反向传播得出delta,那么此时梯度下降就可以进行了,就可以对w进行更新了。如果每次只针对一个点这样做,只会向梯度的方向移动一点,那么其实常常我们会一次随机取很多样本点,一次选取100个点进行1-3的过程,在求出偏导的平均值带入第四不,对w进行更新往往效果会更好!
台湾大学机器学习笔记——Neural Network 神经网络
最新推荐文章于 2022-10-28 12:01:30 发布























 2522
2522

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








