【Python实战因果推断】62_随机实验与统计知识4

目录

The Standard Error of Our Estimates

Confidence Intervals

---

The Standard Error of Our Estimates

在“最危险的方程”中，你将处理效应的平均值估算为治疗组和未治疗组平均值之间的差异。具体来说，你计算了两种交叉销售电子邮件对转化率的平均处理效应。然后你发现，短邮件的效果非常显著，提升了超过8个百分点，而长邮件的影响较小，仅增加了1.3个百分点。但仍然有一个悬而未决的问题：这些效应是否足够大，让你有信心它们不是由偶然造成的？在技术术语中，你是否知道它们是否在统计学上是显著的？

要做到这一点，你首先需要根据我之前展示的方程来估计标准误差(SE)。n相对容易获得。你只需要每个处理组的长度(len)。或者，你可以使用pandas的groupby函数，然后进行size聚合：

 data = pd.read_csv("./data/cross_sell_email.csv")
 short_email = data.query("cross_sell_email=='short'")["conversion"]
 long_email = data.query("cross_sell_email=='long'")["conversion"]
 email = data.query("cross_sell_email!='no_email'")["conversion"]
 no_email = data.query("cross_sell_email=='no_email'")["conversion"]
 data.groupby("cross_sell_email").size()
 
 cross_sell_email
 long 109
 no_email 94
 short 120
 dtype: int64

要得到标准偏差的估计值，您可以应用以下公式：

幸运的是，大多数编程软件已经为你实现了这些功能。在pandas中，你可以使用std方法来计算标准差。将所有这些放在一起，你可以得到以下用于计算标准误差的函数：

 def se(y: pd.Series):
 return y.std() / np.sqrt(len(y))
 print("SE for Long Email:", se(long_email))
 print("SE for Short Email:", se(short_email))
 
 SE for Long Email: 0.021946024609185506
 SE for Short Email: 0.030316953129541618

了解这个公式非常有用（相信我，我们会多次回到这个话题），但你也应该知道，pandas本身就有内置的方法来计算均值的标准误差，那就是.sem()方法： 

 print("SE for Long Email:", long_email.sem())
 print("SE for Short Email:", short_email.sem())
 SE for Long Email: 0.021946024609185506
 SE for Short Email: 0.030316953129541618

Confidence Intervals

你的估计的标准误差是一种信心度量。要精确理解其含义，你需要深入到复杂且有争议的统计学领域。从一种统计学观点来看，即频率主义观点，我们可以说我们的数据不过是底层数据生成过程的一种表现形式。这一过程是抽象且理想的，由真实的参数支配，这些参数不变但对我们来说是未知的。在交叉销售电子邮件的上下文中，如果你能运行多次实验并对每次实验的转化率进行计算，这些转化率会围绕着真实的底层转化率分布，尽管并不完全等于它。这非常类似于柏拉图在《理想国》中对理念论的描述：

每一个[基本形式]都以各种组合的形式显现出来，与行动、物质事物以及彼此相互作用，每一个似乎都是多样的。

为了理解这一点，假设你拥有短版交叉销售电子邮件的转化率真实抽象分布。因为转化率要么是零要么是一，它遵循伯努利分布，假设在这个分布中成功的概率是0.08。也就是说，每当一位顾客收到短版邮件，他们有8%的机会完成转化。接下来，假设你可以运行10,000次实验。在每一次实验中，你收集100位顾客的样本，给他们发送短版邮件并观察平均转化率，总共得到10,000个转化率。这10,000个来自实验的转化率会分布在真实平均值0.08周围。有些实验的转化率会低于真实值，有些则会高于真实值，但是10,000个转化率的平均值将非常接近真实平均值。

 n = 100
 conv_rate = 0.08
 def run_experiment():
 return np.random.binomial(1, conv_rate, size=n)
 np.random.seed(42)
 experiments = [run_experiment().mean() for _ in range(10000)]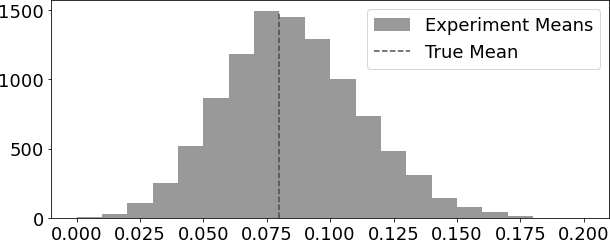

这就意味着你永远不能确信你的实验平均值能准确匹配那个真实的、柏拉图式的理想平均值。然而，利用标准误，你可以创建一个区间，在你运行的95%的实验中这个区间会包含真实的平均值。 在现实生活中，你没有机会用多个数据集来重复同一个实验。你往往只有一个数据集。但是，你可以从模拟多次实验的概念中借鉴思路来构建置信区间。置信区间通常附带有一个概率值，最常见的就是95%的概率。这个概率告诉你，如果你能够运行多次实验并在每一次实验中都构造出95%的置信区间，那么真实的平均值将会落在这个区间内的比例达到95%。

计算置信区间需要用到统计学中最令人震撼的结果之一：中心极限定理。再仔细观察一下你刚刚绘制的转化率分布图。现在回想一下，转化率要么是0，要么是1，因此它遵循伯努利分布。如果你把这个伯努利分布在直方图上绘出，你会看到一个很高的柱子在0的位置，一个小柱子在1的位置，因为成功率只有8%。这看起来和正态分布完全不一样，对吧？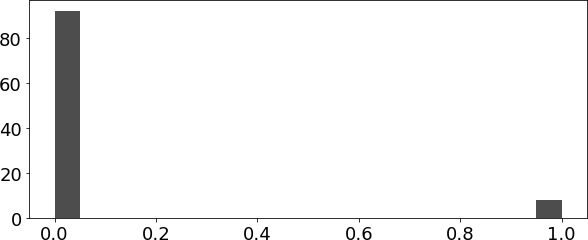

这就是那个令人震惊的统计学原理发挥作用的地方。尽管数据的分布可能不是正态分布（就像转化率的情况，它遵循的是伯努利分布），但是数据的平均值总是遵循正态分布。如果你多次收集转化率的数据，并每次都计算平均转化率，这些平均值将呈现出正态分布。这是非常精妙的，因为正态分布是非常知名的，你可以用它来做各种有趣的事情。 例如，在计算置信区间时，你可以利用统计学理论的知识，即正态分布的95%的数据集中在平均值上下两个标准差（技术上是1.96倍的标准差，但2倍标准差是一个更容易记忆的好近似值）之内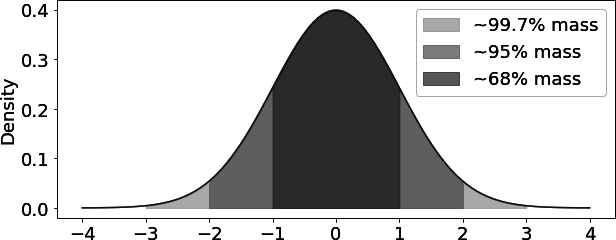

回到你的交叉销售实验，你现在知道如果能运行多次相似的实验，转化率将遵循正态分布。对于那个未知分布的均值，你目前最好的估计就是来自小规模实验的均值。此外，标准误作为样本均值所在未知分布的标准差的估计。因此，如果你将标准误乘以2，然后从实验均值中加减这个值，你就可以构建出一个真值均值的95%置信区间：

 exp_se = short_email.sem()
 exp_mu = short_email.mean()
 ci = (exp_mu - 2 * exp_se, exp_mu + 2 * exp_se)
 print("95% CI for Short Email: ", ci)
 
 95% CI for Short Email: (0.06436609374091676, 0.18563390625908324)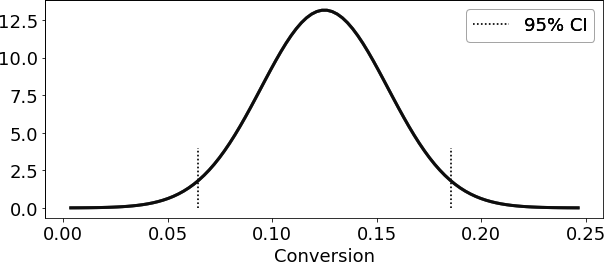

当然，你不必局限于95%的置信区间。如果你想更加谨慎，你可以生成99%的置信区间。你只需要将标准差乘以包含正态分布99%数据量的那个因子即可。

为了找到那个因子，你可以使用scipy库中的ppf函数。这个函数给出了标准正态分布累积分布函数（CDF）的逆函数。例如，ppf(0.5)会返回0.0，这意味着标准正态分布的50%数据在0.0以下。所以，对于任何显著性水平α，你需要乘以标准误以得到1 - α置信区间的因子由给出：

 from scipy import stats
 z = np.abs(stats.norm.ppf((1-.99)/2))
 print(z)
 ci = (exp_mu - z * exp_se, exp_mu + z * exp_se)
 ci
 
 2.5758293035489004
 
 (0.04690870373460816, 0.20309129626539185)
 
 stats.norm.ppf((1-.99)/2)
 
 -2.5758293035489004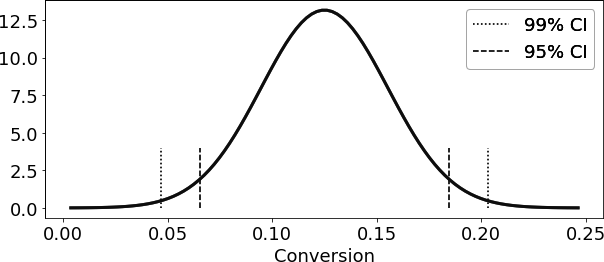

这是针对短邮件而言。你也可以展示其他处理组转化率的95%置信区间：

  def ci(y: pd.Series):
 return (y.mean() - 2 * y.sem(), y.mean() + 2 * y.sem())
 print("95% CI for Short Email:", ci(short_email))
 print("95% CI for Long Email:", ci(long_email))
 print("95% CI for No Email:", ci(no_email))

 95% CI for Short Email: (0.06436609374091676, 0.18563390625908324)
 95% CI for Long Email: (0.01115382234126202, 0.09893792077800403)
 95% CI for No Email: (0.0006919679286838468, 0.08441441505003955)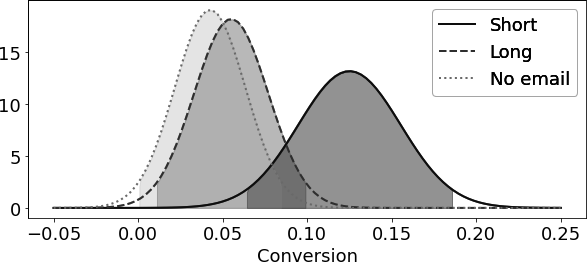

在这里，你可以看到三组的95%置信区间相互重叠。如果不重叠，你就能得出结论说，各组之间的转化率差异不仅仅是偶然的。换句话说，你可以说发送交叉销售邮件会导致转化率有统计学意义上的显著差异。但由于区间确实重叠了，你无法下此结论。至少现在还不能。重要的是，置信区间重叠并不能说明组间差异没有统计学意义，然而，如果它们不重叠，那就意味着存在统计学上的差异。换句话说，非重叠的置信区间是统计显著性的保守证据。

总结一下，置信区间是在你的估计周围放置不确定性的一种方式。样本量越小，标准误越大，因此置信区间也越宽。由于置信区间很容易计算，缺乏置信区间要么表明有不良意图，要么就是缺乏相关知识，这同样令人担忧。最后，你应该对没有任何不确定性度量的测量结果持怀疑态度。

最后一点警告。置信区间的解释比乍看之下要复杂。例如，我不应该说某个特定的95%置信区间包含真实均值的概率是95%。在频率主义统计学中，总体均值被视为一个真实的常数。这个常数要么在某个特定的置信区间内，要么不在。换句话说，一个特定的置信区间要么包含真实均值，要么不包含。如果它包含了真实均值，那么包含它的概率是100%，而不是95%。如果没有包含，概率就是0%。相反，在置信区间中，95%指的是在许多研究中计算出的此类置信区间包含真实均值的频率。95%是我们对用于计算95%置信区间的算法的信心，而不是对特定区间本身的信心。

说到这里，作为一个经济学家（请统计学家们现在回避），我认为这种纯粹主义并没有什么实际用处。实际上，你会看到人们说特定的置信区间有95%的时间包含真实均值。虽然这是错误的，但这并不是很有害，因为它仍然在你的估计中放置了一个直观的不确定性程度。我的意思是，我宁愿你围绕你的估计有一个置信区间，并错误地解释它，也不愿你因害怕误解而避免置信区间。我不在乎你说它们有95%的时间包含真实均值。只是，请永远不要忘记在你的估计周围放置置信区间；否则，你会显得很愚蠢。