题意:
求
思路:
本来出题人想考的不是反演,但是用反演做意外的简单。。
原式:
做反演:
令
易知: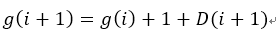
那么可在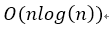
每次查询的复杂度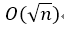
代码:
#include<bits/stdc++.h>
const int N = 1e6+10;
const long long mod = 1e9+7;
using namespace std;
vector<int>pr;
int mu[N],D[N],F[N],fro[N];
bool Np[N];
void init(){
for(int i=1;i<N;i++){
for(int j=i;j<N;j+=i){
D[j]++;
}F[i] = F[i-1] + 1 + D[i-1] ;
if(F[i]>=mod)F[i]-=mod;
fro[i] = fro[i-1] + F[i];
if(fro[i]>=mod)fro[i] -= mod;
}
mu[1] = 1;
for(int i=2;i<N;i++){
if(!Np[i]){
mu[i] = -1;
pr.emplace_back(i);
}for(int j=0,k=pr[0]*i;k<N;k=pr[++j]*i){
Np[k] = true;
if(i%pr[j]==0){
mu[k]=0;
break;
}mu[k] = -mu[i];
}mu[i] += mu[i-1];
}
}
inline long long work(int n){
long long res = 0;
for(int d=1,lastd;d<=n;d=lastd+1){
lastd = n / (n/d);
res = (res + 1LL * ( mu[lastd] - mu[d-1] ) * fro[n/d] ) % mod;
}if(res<0)res+=mod;
return res;
}
int main()
{
init();
int n;
while(scanf("%d",&n)==1){
printf("%I64d\n",work(n));
}return 0;
}








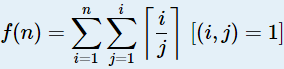
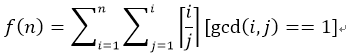

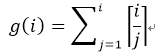
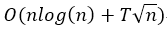














 1974
1974

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








