hdu6134-（莫比乌斯反演）

题解:设f[i]为1-i所有的数被i除后向下取整总和,F[i]为1-i所有数被i除以后向上取整的总和最后满足一个关系：

F[i]=f[i-1]+i;

f[i]=F[i]-i+cnt(cnt为i因子个数)

这里我让f[i]=F[i]重复使用

F[i]=F[i]-F[i/p]{p是i的所有质数因子}那么这里如果多个质数可能重复减了了好几次那么这里就要用容斥原理加回去,那么这里就可以用莫比乌斯反演里面的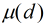函数去掉几个质数共同的部分多减的次数即可

最后把所有前缀都加起来即可

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;
typedef long long int ll;
const int mx = 1e6+5;
const ll mod = 1e9+7;
int u[mx],vis[mx],p[mx];
int F[mx],f[mx];
void init(){
    f[1] = 1;
    F[1] = 1;
    for(int i = 2; i < mx; i++){
        if(!vis[i]) p[++p[0]] = i,u[i] = -1;
        for(int j = 1; j <= p[0]&&i*p[j]<mx; j++){
            vis[p[j]*i] = 1;
            if(i%p[j]==0){
                u[i*p[j]] = 0;
                break;
            }
            else
                u[i*p[j]] = -u[i];
        }
    }
    for(int i = 2; i < mx; i++){
        F[i] = f[i-1]+i;
        int x = i;;
        int ans = 1;
        for(int j = 1; p[j]*p[j] <= i; j++){
            int cnt = 1;
            while(x%p[j]==0){
                x/=p[j];
                cnt++;
            }
            ans*=cnt;
        }
        if(x>1)
            ans *= 2;
        f[i] = F[i]-i+ans;
    }
    for(int i = 2; i < mx; i++)
        f[i] = F[i];
    for(int i = 2; i < mx; i++){
        for(int j = i; j < mx; j+=i)
            if(u[i])
                F[j] += u[i]*f[j/i];
    }
    for(int i = 2; i < mx; i++)
        F[i] = (F[i-1]+F[i])%mod;
}
int main(){
    ll sum = 0;
    init();
    int n;
    while(scanf("%d",&n)!=EOF){
        printf("%d\n",F[n]);
    }
    return 0;
}