Anomaly Detection-异常检测算法（Coursera-Ng-ML课程）

写作本博文只为学习与分享知识。所以如果本系列教程对你有帮助，麻烦不吝在github的项目上点个star吧！非常感谢！

现实生活中有许多需要提前预防一些异常问题出现的情况，例如在飞机起飞前，对飞机各部分进行评估，看发动机等各个零件是否性能正常，若有潜在的问题（可能出现异常情况），则需要及时检修或更换。

那么我们如何去评估异常是否存在呢？

利用联合概率分布~

联合概率分布

$X表示一系列随机变量{X_1,X_2,X_3,…,X_n}的组合,每个随机变量符合服从各自的一种分布。假设各变量是两两相互独立的，那么这些变量的联合概率分布为：
$$P(X)=P(X_1)\ast P(X_2)\ast ....\ast P(X_n)=\Pi P_i$$

即每个随机变量取相应值的概率的乘积。

正态分布

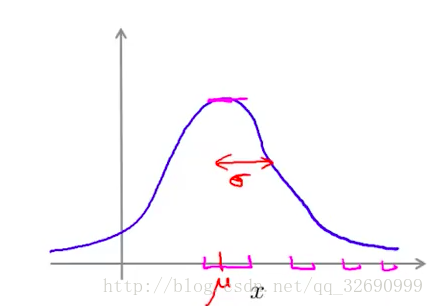
正态分布是一种非常常用的分布函数，其形式如图所示：

图像横轴表示随机变量x的取值，纵轴表示x取相应值的概率(0-1之间)。

该图像的函数形式（概率密度函数）为：

$$y=P(x)=\frac{1}{2\pi \sigma }\ast exp(-\frac{x}{2{\sigma }^2}$$