最小二乘法进行曲线拟合

最小二乘法产生的历史

       最小二乘法最早称为回归分析法。由著名的英国生物学家、统计学家道尔顿（F.Gallton）——达尔文的表弟所创。早年，道尔顿致力于化学和遗传学领域的研究。 他研究父亲们的身高与儿子们的身高之间的关系时，建立了回归分析法。

        父亲的身高与儿子的身高之间关系的研究：1889年，F.Gallton和他的朋友K.Pearson收集了1078个家庭的身高、臂长和腿长的记录（散点图）企图寻找出儿子们身高与父亲们身高之间关系的具体表现形式。从散点图上虽可看出，个子高的父亲确有生出个子高的儿子的倾向，个子低的父亲确有生出个子低的儿子的倾向。但如此一来，高的伸进了天，低的缩入了地。他百思不得其解，同时又发现某人种的平均身高是相当稳定的。最后得到结论：儿子们的身高回复于全体男子的平均身高，即“回归”（见1889年F.Gallton的论文《普用回归定律》）。 后人将此种方法普遍用于寻找变量之间的规律。

        现在，回归分析法已远非道尔顿的本意，已经成为探索变量之间关系最重要的方法，用以找出变量之间关系的具体表现形式。 后来，回归分析法从其方法的数学原理——误差平方和最小出发，改称为最小二乘法。

最小二乘法用于曲线拟合

一、问题提出

       在处理数据时，常要把实验获得的一系列数据点描成曲线表反映物理量间的关系。为了使曲线能代替数据点的分布规律，则要求所描曲线是平滑的，既要尽可能使各数据点对称且均匀分布在曲线两侧。由于目测有误差，所以，同一组数据点不同的实验者可能描成几条不同的曲线(或直线)，而且似乎都满足上述平滑的条件。那么，究竟哪一条是最曲线呢？这一问题就是“曲线拟合”问题。一般来说，“曲线拟合”的任务有两个：

（一）是物理量y与x间的函数关系已经确定，只有其中的常数未定（及具体形式未定）时，根据数据点拟合出各常数的最佳值。

（二）是在物理量y与x间函数关系未知时，从函数点拟合出y与x函数关系的经验公式以及求出各个常数的最佳值。

二、线性拟合

1.一元线性拟合

（1） 函数形式已知

数学推证过程：已知函数为线性关系，其形式为：

                    y=a+bx                    （1）

式中a, b为要用实验数据确定的常数。此类方程叫线性回归方程，方程中的待定常数a, b叫线性回归系数。

由实验测得的数据是x= x1, x2,…，xn时，对应的y值是y= y1,y2,…….yn，

由于实验数据总是存在着误差，所以，把各组数据代入(1)式中，两边并不相等。相应的作图时，数据点也并不能准确地落在公式对应的直线上，如图所示。由图一还可以看出第i个数据点与直线的偏差为：                                                    (1) 如果测量时，使x较之y的偏差很小，以致可以忽略（即Δxi很小 ）时，我们可以认为x的测量是准确的，而数据的偏差，主要是y的偏差，因而有：                                                                                                        ②

我们的目的是根据数据点确定回归常数a和b，并且希望确定的a和b能使数据点尽量靠近直线能使v尽量的小。由于偏差v大小不一，有正有负，所以实际上只能希望总的偏差（    ）最小。 所谓最小二乘法就是这样一个法则，按照这个法则，最好地拟合于各数据点的最佳曲线应使各数据点与曲线偏差的平方和为最小。

由最小二乘法确定a和b

首先，求偏差平方和，将②式两边平方后相加，得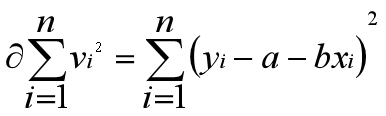：                                                      ③                                                                                   显然，   是a, b的函数。按最小二乘法，当a, b选择适当，能使为最小时y=a+bx才是最佳曲线。

根据二元函数求极值法，把③式对a和b分别求出偏导数。得：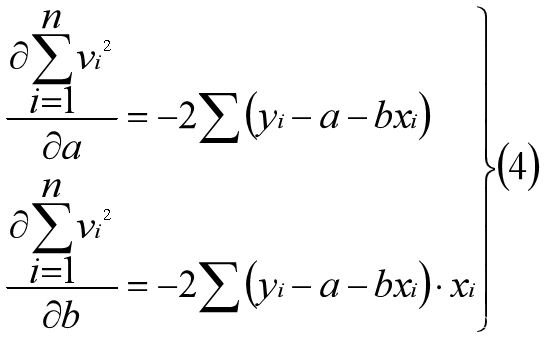

令④等于零，得： 解方程，得：                                         ⑥                                        ⑦ 

公式⑥⑦式中： 从④不难求出对a, b的二阶偏导数为：  

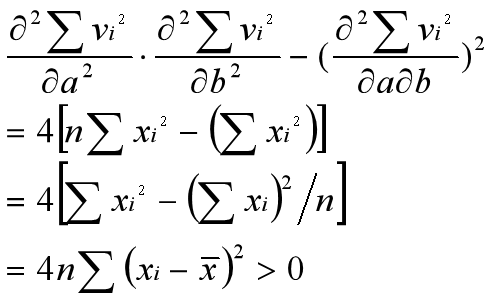
所以⑥⑦式求出的a, b可使为极小值。因而由a, b所确定的曲线y=a+bx就是用最小二乘法拟合的最佳曲线。 由于已知函数形式为非线性时，可用变量代换法“曲线改直”使函数变为线性关系，因而最小二乘法就有更普遍的意义。

2. 经验公式的线性回归—函数形式未知

由于经验公式的函数形式是未知的，因而恰当地选择经验公式的函数形式就成了曲线拟合中的重要问题。 在进行经验公式的回归时，必须先确定函数的形式。确定函数形式一般是根据理论的推断或者从实验数据的变化趋势来推测判断。 如根据实验得到的一组数据     （或其在x y坐标上的数据点）初步判断经验公式为线性关系时，即可用最小二乘法按⑤，⑥式求出b, a值，并进而拟合出直线的线性关系式：     y=a+bx 回归方程。

3. 回归方程的精度和相关系数

用最小二乘法确定a, b存在误差。 总结经验公式时，我们初步分析判断所假定的函数关系是正确，为了解决这些问题，就需要讨论回归方程的精度和相关性。 为了估计回归方程的精度，进一步计算数据点 偏离最佳直线y=a+bx的大小，我们引入概念——剩余标准差，它反映着回归方程与各数据点的拟合程度。

剩余标准差

公式中：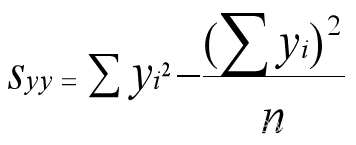

R称为相关系数。其值可正可负，一般有：

a:当R=±1时， =  ,即各数据点与最佳直线完全重合。 b：0<R<1时，各数据点与最佳直线不完全重合。有两种情况： 一种可能是各数据点与该线偏差较小，一种可能是各数据点与该线偏差较大。 当时，减小，一般的数据点越靠近最佳值两旁。两变量间的关系线性相关，可以认为是线性关系，最佳直线所反应的函数关系也越接近两变量间的客观关系。同时还说明了测量的精密度高。 当时，增大，根据数据点的分布，也许能得到一条“最佳”直线。然而，数据点与“最佳”直线的偏差过大。

这时“最佳”二字只能说明数据点距这直线的总偏差较小，但不能反映出数据点的分布规律。或者说，我们事先的初步判断是错误的。数据点的分布规律不是线形的,根本就不能用一条直线表示。 为了帮助我们理解这一点,我们再讨论极限情况。    当 R=0时（最大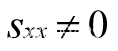） , ,   ,所以b=0,a= , 从而得到y= 的错误结论。这说明数据点的分布不是线性,不能拟合为线性关系曲线。