PATA 1066 Root of AVL Tree（25 分）解题报告

1066 Root of AVL Tree（25 分）

An AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Figures 1-4 illustrate the rotation rules.

 

 

 

 

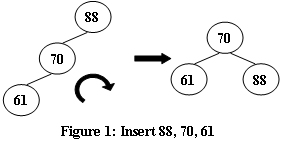
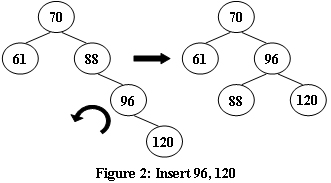
Now given a sequence of insertions, you are supposed to tell the root of the resulting AVL tree.

 

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer N (≤20) which is the total number of keys to be inserted. Then N distinct integer keys are given in the next line. All the numbers in a line are separated by a space.

Output Specification:

For each test case, print the root of the resulting AVL tree in one line.

Sample Input 1:

5
88 70 61 96 120

Sample Output 1:

70

Sample Input 2:

7
88 70 61 96 120 90 65

Sample Output 2:

88

作者: CHEN, Yue

单位: 浙江大学

时间限制: 400 ms

内存限制: 64 MB

代码长度限制: 16 KB

 

题目大意：给定一个序列，这个序列可以唯一的构造一棵AVL树，要求你给出这棵树的根节点

解题思路：按照给定序列构造AVL树，并输出根节点

本题考察AVL树的建立方法，左旋右旋操作以及操作判别

 

AC代码：

#include<iostream>
#include<stdio.h>
#include<stdlib.h>
#include<algorithm>
using namespace std;
struct node
{
	int v;//结点数据 
	int height;//结点高度 
	node *lchild;
	node *rchild;
} *root;

node *newnode(int v)//创建一个新结点，新结点的高度置为1 
{
	node *Node = new node;
	Node->v=v;
	Node->height=1;
	Node->lchild=Node->rchild=NULL;
	return Node;
}

int getHeight(node *root)//获得当前结点高度 
{
	if(root==NULL)
	return 0;
	return root->height;
}

void updateHeight(node *root)//更新当前根节点高度 
{
	root->height=max(getHeight(root->lchild),getHeight(root->rchild))+1;
}

int getBalanceFactor(node *root)//获取平衡因子，通过左子树-右子树高度 
{
	return getHeight(root->lchild)-getHeight(root->rchild);
}
//左旋，temp指向根节点的右子树，共有三个步骤 
//1.让temp的左子树成为root的右子树
//2.让root成为temp的左子树
//3.将temp设置为新的root 
void L(node* &root)//采用node* &root是为了使root作为一个指针进行操作 
{
	node *temp=root->rchild;
	root->rchild=temp->lchild;
	temp->lchild=root;
	updateHeight(root);
	updateHeight(temp);
	root=temp;
}

void R(node* &root)
{
	node *temp=root->lchild;
	root->lchild=temp->rchild;
	temp->rchild=root;
	updateHeight(root);
	updateHeight(temp);
	root=temp;
}
//左旋和右旋是互逆操作，把所有的left换成right，right换成left就行了 
void insert(node* &root,int v)//按BST规则插入，并进行适当操作使得该树始终是AVL树 
{
	if(root==NULL)
	{
		root=newnode(v);
		return;
	}
	if(v<root->v)
	{
		insert(root->lchild,v);
		updateHeight(root);//注意不要忘记更新结点高度 
		if(getBalanceFactor(root)==2)
		{
			if(getBalanceFactor(root->lchild)==1)//LL
			{
				R(root);
			}
			else if(getBalanceFactor(root->lchild)==-1)//LR
			{
				L(root->lchild);
				R(root);
			}
		}
	}
	else
	{
		insert(root->rchild,v);
		updateHeight(root);
		if(getBalanceFactor(root)==-2)
		{
			if(getBalanceFactor(root->rchild)==-1)//RR
			{
				L(root);
			}
			else if(getBalanceFactor(root->rchild)==1)//RL
			{
				R(root->rchild);//RL情况经过一次右旋会变为RR，然后左旋即可 
				L(root);
			}
		}
	}
}
int main()
{
	int n,data;
	cin>>n;
	for(int i;i<n;i++)
	{
		cin>>data;
		insert(root,data);
	}
	cout<<root->v<<endl;
	return 0;
}